Integrali multipli (o doppi)
Cosa sono gli integrali multipli
Gli integrali multipli (integrali doppi o multidimensionali) sono integrali definiti di funzioni di due o più variabili (dimensioni). $$ \int f(x,y) \ dx \ dy $$ $$ \int f(x,y,z) \ dx \ dy \ dz $$
Gli integrali a due variabili dimensioni sono anche detti integrali doppi. Quelli a tre variabili sono detti integrali tripli.
A cosa serve?
L'integrale doppio di una funzione a due variabili misura il volume del solido sommando le superfici della funzione nei piani del suo dominio.
Nota. Gli integrali a due o più dimensioni (variabili) hanno le stesse proprietà degli integrali definiti a una dimensione (variabile).
L'integrale doppio
L'integrale multiplo di una funzione f(x,y) a due variabile (due dimensioni) è detto integrale doppio.
Spesso si indica con doppio simbolo integrale.
$$ \int f(x,y) \ dx \ dy = \iint f(x,y) \ dx \ dy $$
In un integrale doppio la regione di integrazione della funzione f(x,y) viene suddivisa in piccoli quadrati sommati tra loro.
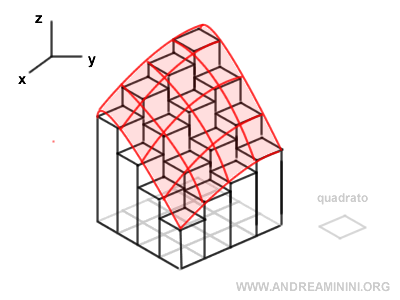
Il valore a cui tende la somma quando la superficie dei quadrati è infinitesimale (ossia tende a zero) è il valore dell'integrale.
L'integrale triplo
L'integrale multiplo di una funzione f(x,y,z) a tre variabili (tre dimensioni) è detto integrale triplo.
Spesso si indica con il triplo simbolo dell'integrale.
$$ \int f(x,y,z) \ dx \ dy \ dz = \iiint f(x,y,z) \ dx \ dy \ dz $$
In un integrale triplo la regione di integrazione della funzione f(x,y,z) viene suddivisa in piccoli cubi, poi sommati tra loro.
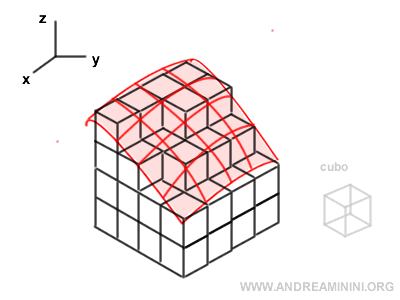
Il valore a cui tende la somma quando il volume dei cubi è infinitesimale (ossia tende a zero) è il valore dell'integrale.
E così via.
