Il teorema di Rouché-Capelli
Il teorema di Rouché-Capelli mi permette di capire se esistono e quante sono le soluzioni del sistema lineare.
Un sistema di equazioni lineare ha una o più soluzioni se e soltanto se il rango della matrice dei coefficienti A è uguale al rango della matrice completa A|B.
$$ rg(A) = rg(A|B) $$
Viceversa, se il rango della matrice dei coefficienti è diverso dal rango della matrice completa A|B il sistema di equazioni lineari non è risolvibile ossia non ha soluzioni.
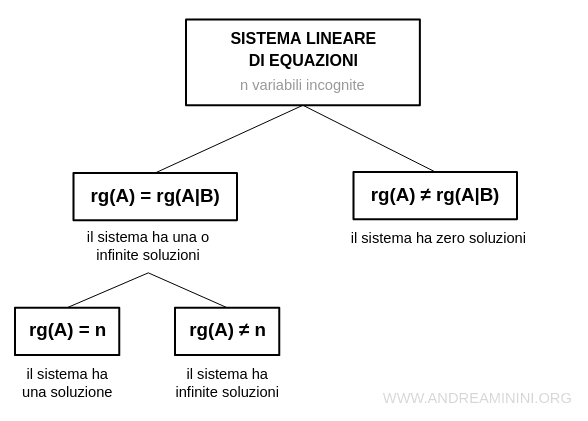
Una volta confermata l'esistenza delle soluzioni, il teorema dà anche indicazioni per conoscere quante sono.
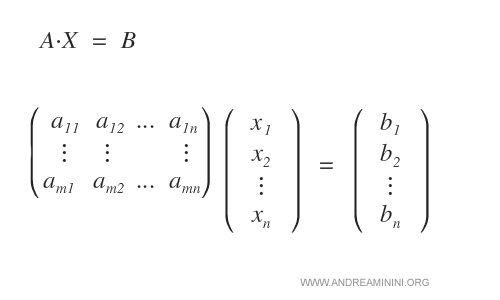
Se il sistema ammette soluzioni, il numero delle soluzioni è uguale a infinito elevato n-r. Dove n è il numero delle variabili incognite del sistema lineare e r è il rango della matrice A. $$ \infty^{n-r} $$
Il teorema di Rouché-Capelli è utile nella risoluzione dei sistemi lineari perché mi permette di capire se l'equazione ha una, nessuna o infinite soluzioni
In ogni caso il teorema di Rouché-Capelli non dice quali sono le soluzioni ma solo se esistono.
Un esempio pratico
Il seguente sistema è composto da due incognite (n=2).
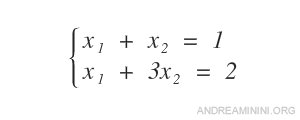
Riscrivo il sistema sotto forma di matrici.

Entrambe le matrici hanno un rango uguale a due (r). Quindi, il sistema ha delle soluzioni.
In particolar modo, il sistema ha una soluzione poiché il numero delle incognite n=2 è uguale al rango r=2.

Dimostrazione
Il sistema AXB può essere scritto sotto forma di una combinazione lineare di vettori.
$$ x_1 \cdot v_1 + ... + x_n \cdot v_n = B $$
Dove
- X è il vettore delle incognite ( soluzioni del sistema ). $$ X = ( x_1,...,x_n ) $$
- V è il sottospazio vettoriale di Rm dei vettori numerici che compongono la matrice dei coefficienti A $$ V = ( v_1,...,v_n ) $$
- B è il vettore dei termini noti $$ B = ( b_1,...,b_n ) $$
Secondo le proprietà della dipendenza lineare dei vettori, il sistema ammette delle soluzioni {x1,...,xn} soltanto se V e B sono vettori linearmente dipendenti.
$$ ( v_1 , ... , v_n , B ) $$
Ossia, se il rango della matrice completa A|B eguaglia il rango della matrice dei coefficienti A
$$ rg(A|B) = rg(A) $$
In tali casi
$$ B \in V $$
Nota. Se il rango rg(A|B) è diverso da rg(A), allora i vettori v1,..vn,B sono linearmente indipendenti, il vettore B non appartiene a V e il sistema è incompatibile.
Osservazioni utili
Il teorema di Rouché Capelli è particolarmente utile nella risoluzione dei sistemi di equazioni lineari quando è abbinato al teorema di Cramer.
Secondo il teorema di Cramer un sistema lineare ha una e una sola soluzione se il determinante della matrice dei coefficienti è diverso da zero (Δ≠0).
Viceversa, se il determinante è uguale a zero (Δ=0) il sistema non ha una soluzione. Potrebbe non averne (0 soluzioni) o averne infinite (inf soluzioni). Il teorema di Cramer non dice nulla a riguardo.
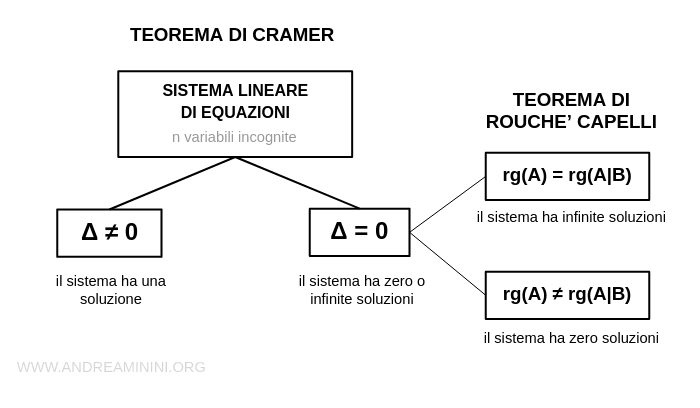
Se il determinante è nullo (Δ=0) posso usare il teorema di Rouché-Capelli per capire se il sistema non ha soluzioni (0 soluzioni) o ne ha infinite (∞ soluzioni).
Combinando i due teoremi posso sapere esattamente il numero di soluzioni del sistema lineare.
Tuttavia, non è sempre possibile usare Cramer e Rouché Capelli.
Il teorema di Cramer è utilizzabile solo se la matrice dei coefficienti è quadrata e questo accade se il sistema ha un numero di equazioni uguale al numero delle variabili incognite (m=n).
Inoltre, il teorema di Rouché-Capelli è utile se il sistema lineare ha poche equazioni.
E' invece poco utilizzabile se il sistema lineare ha decine di equazioni perché il calcolo del determinante e del rango diventa molto più complesso al crescere delle dimensioni delle matrici.
Nota. In generale preferisco risolvere i sistemi di equazioni lineari più complessi con il metodo di Gauss-Jordan cercando di trasformare la matrice completa A|B in una matrice a gradini. Questo metodo è applicabile a sistemi di equazioni con qualsiasi numero di equazioni e di incognite. E' particolarmente utile quando il calcolo del rango diventa difficile.
E così via.
