Il fascio proprio e improprio di piani

La differenza tra i fasci di piani propri e impropri nello spazio.

Fascio proprio di piano

Data una retta r un fascio proprio di piani è un insieme di piani che contengono la retta r. $$ λ_1 ( a_1x+b_1y+c_1z+d_1 ) + λ_2 ( a_2x+b_2y+c_2z+d_2 ) = 0 $$ $$ ( a_1x+b_1y+c_1z+d_1 ) + \frac{λ_2}{λ_1} ( a_2x+b_2y+c_2z+d_2 ) = 0 $$

Le due equazioni generano due piani distinti.

Il punto di intersezione dei piani è la retta r.

$$ \begin{cases} λ_1 ( a_1x+b_1y+c_1z+d_1 ) \\ λ_2 ( a_2x+b_2y+c_2z+d_2 ) \end{cases} $$

Esempio

Ho l'equazione di una retta nello spazio, conosco già le due equazioni del piano da usare.

$$ \begin{cases} 2x+3y+8z+2=0 \\ -4x-6y+6z-12=0 \end{cases} $$

I punti della retta sono l'insieme dei punti di intersezione di due piani.

In questo caso il fascio proprio di piani è determinato dal sistema

$$ ( 2x+3y+8z+2 ) + \frac{λ_2}{λ_1} ( -4x-6y+6z-12 ) = 0 $$

Dove λ₁ e λ₂ sono due scalari qualsiasi purché λ₂ sia diverso da 0.

Per semplicità posso indicare il rapporto come k = λ₂/λ₁

$$ ( 2x+3y+8z+2 ) + k ( -4x-6y+6z-12 ) = 0 $$

Cambiando il valore k ottengo tutti i piani inclinati sulla retta.

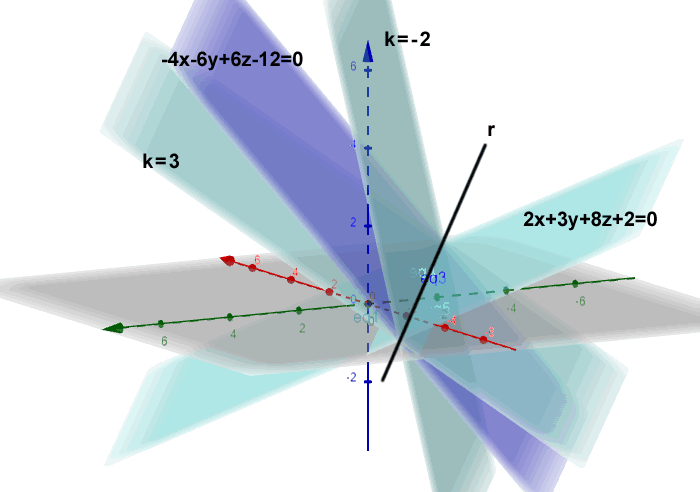
E' il fascio proprio di piani della retta r.

Fascio improprio di piano

Dato un piano A un fascio improprio di piani è un insieme di piani paralleli al piano A. $$ ax+by+cz+d=0 $$

Per ottenere i piani paralleli, basta modificare il parametro d.

I coefficienti a,b,c non devono essere tutti contemporaneamente nulli.

Esempio

L'equazione di un piano nello spazio è

$$ 2x+3y+8z+2=0 $$

Modificando il parametro k ottengo tutti i piani paralleli.

$$ 2x+3y+8z+k=0 $$

Con k=-12 e k=-25 la rappresentazione grafica è la seguente

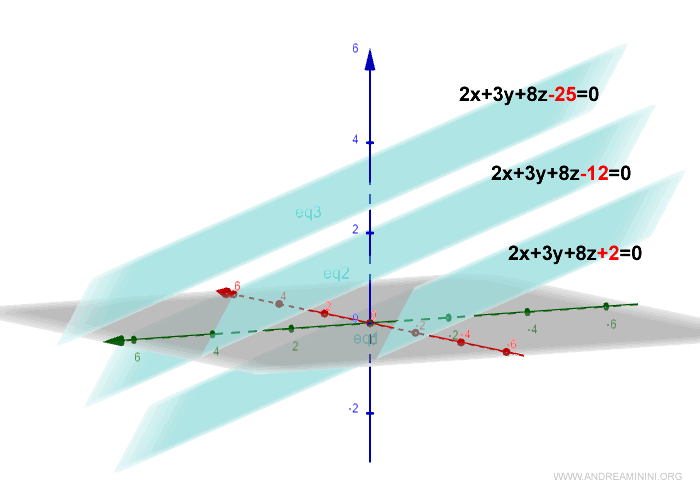
E così via.