Esercizio calcolo integrale 28
Devo risolvere l'integrale
$$ \int \frac{x^3+2x-3}{x^2+2x+1} \ dx $$
La funzione integranda è una funzione fratta con un rapporto tra due polinomi.
Il polinomio al denominatore è di grafo inferiore al polinomio al numeratore. Quindi, posso semplificare la funzione integranda tramite la divisione dei due polinomi.
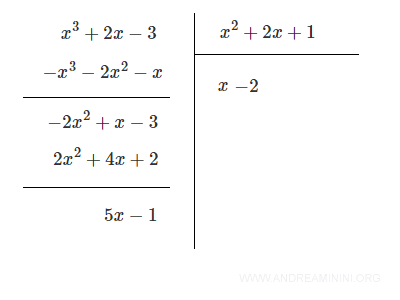
Il quoziente è il polinomio (x-2) con resto (5x-1)
$$ \frac{x^3+2x-3}{x^2+2x+1} = x - 2 \ \ \ con \ resto \ \ 5x - 1 $$
Pertanto, posso scrivere il polinomio al numeratore (x3+2x-3) come il prodotto del polinomio al denominatore (x2+2x+1) per il polinomio quoziente (x-2) più il polinomio resto (5x-1)
$$ x^3+2x-3 = (x^2+2x+1) \cdot (x - 2) + (5x-1) $$
Ora nell'intelgrale sostituisco il polinomio al denominatore con l'espressione appena trovata
$$ \int \frac{x^3+2x-3}{x^2+2x+1} $$
$$ \int \frac{(x^2+2x+1) \cdot (x - 2) + (5x-1)}{x^2+2x+1} \ dx $$
Sapendo che l'integrale di una somma è la somma degli integrali
$$ \int \frac{(x^2+2x+1) \cdot (x - 2) }{x^2+2x+1} \ dx + \int \frac{5x-1}{x^2+2x+1} \ dx $$
$$ \int x-2 \ dx + \int \frac{5x-1}{x^2+2x+1} \ dx $$
Il primo integrale è elementare e lo risolvo facilmente
$$ \frac{(x-2)^2}{2} + c + \int \frac{5x-1}{x^2+2x+1} \ dx $$
$$ \frac{x^2-4x+4}{2} + c + \int \frac{5x-1}{x^2+2x+1} \ dx $$
$$ \frac{x^2}{2} - 2x + 2 + c + \int \frac{5x-1}{x^2+2x+1} \ dx $$
I termini +2 e +c sono due costanti, quindi posso semplificare l'espressione scrivendo solo +c
$$ \frac{x^2}{2} - 2x + c + \int \frac{5x-1}{x^2+2x+1} \ dx $$
Mi resta da risolvere il secondo integrale.
La funzione integranda è il rapporto tra due polinomi non più divisibili tra loro perché il polinomio al denominatore è di grado superiore.
Il denominatore x2+2x+1 è un quadrato di un binomio (x+1)2
$$ \frac{x^2}{2} - 2x + c + \int \frac{5x-1}{(x+1)^2} \ dx $$
Per semplificare la funzione integranda utilizzo la scomposizione in fratti semplici
$$ \int \frac{5x-1}{(x+1)^2} \ dx = \int \frac{A}{(x+1)^2} + \frac{B}{x+1} \ dx $$
$$ \int \frac{5x-1}{(x+1)^2} \ dx = \int \frac{A+B \cdot (x+1)}{(x+1)^2} \ dx $$
$$ \int \frac{5x-1}{(x+1)^2} \ dx = \int \frac{A+Bx+B}{(x+1)^2} \ dx $$
I denominatori sono uguali in entrambi i membri.
Quindi, posso dedurre per confronto che Bx=5x e A+B=-1
Per trovare i coefficienti A, B, C scrivo il sistema di equazioni
$$ \begin{cases} A+B=-1 \\ \\ Bx=5x \end{cases} $$
Applico la proprietà invariantiva e divido entrambi i membri della seconda equazione per x
$$ \begin{cases} A+B=-1 \\ \\ \frac{Bx}{x}=\frac{5x}{x} \end{cases} $$
$$ \begin{cases} A+B=-1 \\ \\ B=5 \end{cases} $$
Risolvo il sistema per sostituzione sapendo che B=5
$$ \begin{cases} A+5=-1 \\ \\ B=5 \end{cases} $$
$$ \begin{cases} A=-1-5 \\ \\ B=5 \end{cases} $$
$$ \begin{cases} A=-6 \\ \\ B=5 \end{cases} $$
Ho trovato i coefficienti A=-6, B=5
Sapendo che
$$ \int \frac{5x-1}{(x+1)^2} \ dx = \int \frac{A}{(x+1)^2} + \frac{B}{x+1} \ dx $$
Per la proprietà lineare degli integrali
$$ \int \frac{5x-1}{(x+1)^2} \ dx = \int \frac{A}{(x+1)^2} \ dx + \int \frac{B}{x+1} \ dx $$
Sostituisco A=-6 e B=5
$$ \int \frac{5x-1}{(x+1)^2} \ dx = \int \frac{-6}{(x+1)^2} \ dx + \frac{5}{x+1} \ dx $$
Gli integrali nel membro di destra sono elementari
$$ \int \frac{5x-1}{(x+1)^2} \ dx =- 6 \int \frac{1}{(x+1)^2} \ dx + 5 \frac{1}{x+1} \ dx $$
Il secondo integrale è 5∫x+1 dx = 5·log|x+1|+c
$$ \int \frac{5x-1}{(x+1)^2} \ dx =- 6 \int \frac{1}{(x+1)^2} \ dx + 5 \log |x+1| + c $$
Il primo integrale è -6∫x+1 dx = 6/(x+1)+c
$$ \int \frac{5x-1}{(x+1)^2} \ dx = \frac{6}{x+1} + 5 \log |x+1| + c $$
Spiegazione. L'integrale $$ \int \frac{1}{(x+1)^2} \ dx $$ si ottiene derivando l'espressione $$ D[ \frac{1}{x+1} ] = \frac{D[1] \cdot (x+1) - 1 \cdot D[x+1] }{(x+1)^2} = \frac{0 \cdot (x+1) - 1 \cdot 1}{(x+1)^2} = \frac{- 1}{(x+1)^2} $$ Pertanto $$ - 6 \int \frac{1}{(x+1)^2} \ dx = -6 \cdot \frac{- 1}{(x+1)^2} + c = \frac{6}{(x+1)^2} + c $$
Una volta risolto l'ultimo integrale lo sostituisco all'esercizio
$$ \frac{x^2}{2} - 2x + c + \int \frac{5x-1}{x^2+2x+1} \ dx $$
$$ \frac{x^2}{2} - 2x + c + \int \frac{5x-1}{(x+1)^2} \ dx $$
$$ \frac{x^2}{2} - 2x + \frac{6}{x+1} + 5 \log |x+1| + c $$
In conclusione, la soluzione dell'integrale è
$$ \int \frac{x^3+2x-3}{x^2+2x+1} \ dx = \frac{x^2}{2} - 2x + \frac{6}{x+1} + 5 \log |x+1| + c $$
E così via.
