Integrazione delle funzioni razionali tramite fratti semplici

L'integrazione per fratti semplici è una tecnica di semplificazione utile quando la funzione integranda è una funzione razionale $$ \int \frac{P(x)}{Q(x)} $$ Dove P(x) e Q(x) sono due polinomi e P(x) è di grado inferiore o uguale a Q(x).

Se il polinomio al numeratore Pn(x) è di grado inferiore o uguale x≤m al polinomio al numeratore Q(x)

$$ \int \frac{P(x)_n}{Q(x)_m} \ dx $$

Nota. Qualsiasi rapporto di polinomi è sempre riconducibile tramite la divisione tra polinomi al caso in cui il polinomio al numeratore Pn(x) è di grado inferiore o uguale x<=m al polinomio al numeratore Q(x)

Posso decomporre la funzione razionale P(x)/Q(x) a seconda se il polinomio al denominatore Q(x) ha radici reali di molteplicità pari a 1 o superiore, oppure radici complesse.

• Se il polinomio al denominatore Q(x) è scomponibile nei numeri reali in (x-a) oppure in (x-a)ⁿ o nella forma più generale ax+b. Ad esempio 3(x-2)=3x-6.
  • Ogni fattore x-a viene sostituito con una frazione fraziale del tipo $$ \frac{A}{(x-a)} $$
  • Ogni fattore (x-a)ⁿ con molteplicità maggiore di uno (n>1) è sostituito con frazioni parziali incrementando l'esponente al denominatore da 1 a n $$ \frac{A}{(x-1)} + \frac{B}{(x-1)^2} +...+ \frac{C}{(x-1)^n} $$

  Nota. Ogni polinomio ax²+bx+c con radici reali x₁ e x₂ (Δ≥0) è sempre scomponibile nella forma a·(x-x₁)·(x-x₂). Per un approfondimento leggere gli appunti sulla scomposizione di un trinomio di 2° grado.

• Se il polinomio al denominatore del tipo ax²+bx+c non è scomponibile nei numeri reali perché il discriminante è negativo (Δ<0). In questi casi il polinomio ha radici nei numeri complessi. Ad esempio, x²+1 oppure (x²+1)ⁿ rientrano in questa forma.
  • Ogni fattore ax²+bx+c non scomponibile è sostituito con una frazione parziale del tipo $$ \frac{Ax+B}{ax^2+bx+c}$$
  • Ogni fattore (ax²+bx+c)ⁿ con molteplicità maggiore di uno (n>1) è sostituito con frazioni parziali incrementando gli esponenti al denominatore da 1 a n. $$ \frac{Ax+B}{(ax^2+bx+c)} + \frac{Cx+D}{(ax^2+bx+c)^2} +...+ \frac{Ex+F}{(ax^2+bx+c)^n} $$

Per spiegarlo meglio farò degli esempi pratici

A] Il polinomio al denominatore ha radici reali di molteplicità 1

Devo risolvere l'integrale

$$ \int \frac{x-1}{x^2+3x} \ dx $$

La funzione integranda è una funzione razionale con un polinomio al numeratore di grado inferiore al denominatore, pertanto non posso dividere i polinomi.

Scompongo il polinomio al denominatore per fattorizzazione, mettendo in evidenza la x

$$ \int \frac{x-1}{x \cdot (x+3)} \ dx $$

In questo caso la molteplicità delle radici è pari a uno perché (x+3)¹ e x¹. Quindi, le radici x=-3 e x=0 hanno molteplicità uguali a uno.

Poi trasformo il rapporto in una somma di fratti semplici dove A e B sono costanti ancora da individuare

$$ \int \frac{x-1}{x \cdot (x+3)} \ dx = \int \frac{A}{x} + \frac{B}{x+3} \ dx $$

$$ \int \frac{x-1}{x \cdot (x+3)} \ dx = \int \frac{A \cdot (x+3) + B \cdot x}{x \cdot (x+3)} $$

$$ \int \frac{x-1}{x \cdot (x+3)} \ dx = \int \frac{Ax+3A + Bx}{x \cdot (x+3)} $$

Metto in evidenza l'incognita x

$$ \int \frac{x-1}{x \cdot (x+3)} \ dx = \int \frac{x \cdot (A+B) +3A}{x \cdot (x+3)} $$

I due membri dell'equazione hanno lo stesso denominatore x(x+3)

Osservo i termini al numeratore e deduco per confronto che x=x(A+B) e -1=3A

Questo mi permette di scrivere un sistema di equazioni per trovare i valori delle costanti A e B

$$ \begin{cases} x = x \cdot (A+B) \\ \\ -1 = 3A \end{cases} $$

Applico la proprietà invariantiva e divido entrambi i membri della prima equazione per x

$$ \begin{cases} \frac{x}{x} = \frac{x \cdot (A+B)}{x} \\ \\ -1 = 3A \end{cases} $$

$$ \begin{cases} 1 = A+B \\ \\ -1 = 3A \end{cases} $$

Risolvo il sistema per sostituzione

$$ \begin{cases} 1 = A+B \\ \\ A = -\frac{1}{3} \end{cases} $$

$$ \begin{cases} 1 = - \frac{1}{3} + B \\ \\ A = -\frac{1}{3} \end{cases} $$

$$ \begin{cases} B = 1 + \frac{1}{3} \\ \\ A = -\frac{1}{3} \end{cases} $$

$$ \begin{cases} B = \frac{4}{3} \\ \\ A = -\frac{1}{3} \end{cases} $$

Ho trovato i valori delle costanti A=-1/3 e B=4/3

Sostituisco i valori appena trovati nell'integrale della somma

$$ \int \frac{x-1}{x \cdot (x+3)} \ dx = \int \frac{A}{x} + \frac{B}{x+3} \ dx $$

$$ \int \frac{x-1}{x \cdot (x+3)} \ dx = \int \frac{- \frac{1}{3}}{x} + \frac{\frac{4}{3}}{x+3} \ dx $$

$$ \int \frac{x-1}{x \cdot (x+3)} \ dx = \int -\frac{1}{3x} + \frac{4}{3(x+3)} \ dx $$

Per la proprietà lineare degli integrali, l'integrale di una somma è uguale alla somma degli integrali

$$ \int \frac{x-1}{x \cdot (x+3)} \ dx = \int -\frac{1}{3x} \ dx + \int \frac{4}{3(x+3)} \ dx $$

$$ \int \frac{x-1}{x \cdot (x+3)} \ dx = - \frac{1}{3} \int \frac{1}{x} \ dx + \frac{4}{3} \int \frac{1}{x+3} \ dx $$

In questo modo ho ricondotto lo studio dell'integrale iniziale (membro di sinistra) allo studio di due integrali composti da fratti semplici (membro a destra).

Gli integrali a destra sono facilmente risolvibili

L'integrale di ∫1/x = log|x|+c

$$ \int \frac{x-1}{x \cdot (x+3)} \ dx = - \frac{1}{3} \log|x|+c + \frac{4}{3} \int \frac{1}{x+3} \ dx $$

L'integrale di ∫1/(x+3) = log|x+3|+c

$$ \int \frac{x-1}{x \cdot (x+3)} \ dx = - \frac{1}{3} \log|x|+ \frac{4}{3} \log |x+3| + c $$

Ho così risolto l'integrale a sinistra tramite la tecnica dei fratti semplici.

B] Il polinomio al denominatore ha radici di molteplicità 2

Devo risolvere l'integrale

$$ \int \frac{2x+5}{(x+1) \cdot (x+3)^2 } \ dx $$

Le radici al denominatore sono x=-1 e x=-3, la prima radice (x=1) ha molteplicità uno mentre la seconda radice (x=-3) ha molteplicità due.

In questo caso per la seconda radice devo considerare due fratti semplici, uno con denominatore (x+3) e l'altro con denominatore (x+3)²

$$ \int \frac{2x+5}{(x+1) \cdot (x+3)^2 } \ dx = \int \frac{A}{x+1} + \frac{B}{x+3} + \frac{C}{(x+3)^2} \ dx $$

$$ \int \frac{2x+5}{(x+1) \cdot (x+3)^2 } \ dx = \int \frac{A}{x+1} + \frac{B}{x+3} + \frac{C}{(x+3)^2} \ dx $$

$$ \int \frac{2x+5}{(x+1) \cdot (x+3)^2 } \ dx = \int \frac{A \cdot (x+3)^2 + B \cdot (x+1) \cdot (x+3) + C \cdot (x+1) }{(x+1) \cdot (x+3)^2} \ dx $$

$$ \int \frac{2x+5}{(x+1) \cdot (x+3)^2 } \ dx = \int \frac{A \cdot (x^2+6x+9) + B \cdot (x^2+3x+x+3) + Cx+C}{(x+1) \cdot (x+3)^2} \ dx $$

$$ \int \frac{2x+5}{(x+1) \cdot (x+3)^2 } \ dx = \int \frac{Ax^2+6Ax+9A + Bx^2+3Bx+Bx+3B + Cx+C}{(x+1) \cdot (x+3)^2} \ dx $$

$$ \int \frac{2x+5}{(x+1) \cdot (x+3)^2 } \ dx = \int \frac{Ax^2+6Ax+9A + Bx^2+4Bx+3B + Cx+C}{(x+1) \cdot (x+3)^2} \ dx $$

$$ \int \frac{2x+5}{(x+1) \cdot (x+3)^2 } \ dx = \int \frac{x^2(A+B )+x(6A+4B+C) +9A + 3B +C}{(x+1) \cdot (x+3)^2} \ dx $$

I due membri dell'equazione hanno lo stesso denominatore.

Quindi, posso dedurre per confronto dei numeratori che A+B=0 , 6A+4B+C=2 e 9A+3B+C=5.

Spiegazione. Il coefficiente di x² è zero nel membro di sinistra e (A+B) nel membro di destra. Quindi A+B=0. Il coefficiente di x¹=x è 2 a sinistra e (6A+4B+C) a destra. Quindi 6A+4B+C=2. Il coefficiente di x⁰=1 è 5 a sinistra e 9A+3B+C a destra. Quindi 9A+3B+C=5.

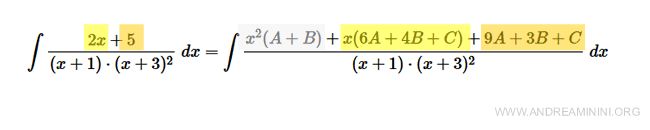
Metto a sistema queste equazioni per trovare i valori delle costanti A,B,C

$$ \begin{cases} A+B=0 \\ 6A+4B+C=2 \\ 9A+3B+C=5 \end{cases} $$

$$ \begin{cases} A=-B \\ 6(-B)+4B+C=2 \\ 9(-B)+3B+C=5 \end{cases} $$

$$ \begin{cases} A=-B \\ -2B+C=2 \\ -6B+C=5 \end{cases} $$

$$ \begin{cases} A=-B \\ C=2+2B \\ -6B+(2+2B)=5 \end{cases} $$

$$ \begin{cases} A=-B \\ C=2+2B \\ -4B=5-2 \end{cases} $$

$$ \begin{cases} A=-B \\ C=2+2B \\ B= - \frac{3}{4} \end{cases} $$

$$ \begin{cases} A=-( -\frac{3}{4} ) \\ C=2+2( -\frac{3}{4} ) \\ B= - \frac{3}{4} \end{cases} $$

$$ \begin{cases} A=\frac{3}{4} \\ C=2 -\frac{3}{2} \\ B= - \frac{3}{4} \end{cases} $$

$$ \begin{cases} A=\frac{3}{4} \\ C=\frac{4-3}{2} \\ B= - \frac{3}{4} \end{cases} $$

$$ \begin{cases} A=\frac{3}{4} \\ C=\frac{1}{2} \\ B= - \frac{3}{4} \end{cases} $$

Una volta trovate le costanti A=3/4, B=-3/4 e C=1/2 le sostituisco ai fratti semplici

$$ \int \frac{2x+5}{(x+1) \cdot (x+3)^2 } \ dx = \int \frac{A}{x+1} + \frac{B}{x+3} + \frac{C}{(x+3)^2} \ dx $$

$$ \int \frac{2x+5}{(x+1) \cdot (x+3)^2 } \ dx = \int \frac{(\frac{3}{4})}{x+1} + \frac{(-\frac{3}{4})}{x+3} + \frac{(\frac{1}{2})}{(x+3)^2} \ dx $$

$$ \int \frac{2x+5}{(x+1) \cdot (x+3)^2 } \ dx = \int \frac{3}{4(x+1)} - \frac{(3}{4(x+3)} + \frac{1}{2(x+3)^2} \ dx $$

Per la proprietà lineare l'integrale di una somma è uguale alla somma degli integrali

$$ \int \frac{2x+5}{(x+1) \cdot (x+3)^2 } \ dx = \int \frac{3}{4(x+1)} \ dx - \int \frac{(3}{4(x+3)} \ dx + \int \frac{1}{2(x+3)^2} \ dx $$

$$ \int \frac{2x+5}{(x+1) \cdot (x+3)^2 } \ dx = \frac{3}{4} \int \frac{1}{(x+1)} \ dx - \frac{3}{4} \int \frac{(1}{(x+3)} \ dx + \frac{1}{2} \int \frac{1}{(x+3)^2} \ dx $$

A questo punto risolvo singolarmente ogni integrale elementare

I primi due integrali sono logaritmi

$$ \int \frac{2x+5}{(x+1) \cdot (x+3)^2 } \ dx = \frac{3}{4} \cdot \log |x+1| + C - \frac{3}{4} \int \frac{(1}{(x+3)} \ dx + \frac{1}{2} \int \frac{1}{(x+3)^2} \ dx $$

$$ \int \frac{2x+5}{(x+1) \cdot (x+3)^2 } \ dx = \frac{3}{4} \cdot \log |x+1| - \frac{3}{4} \log | x+3| + C+ \frac{1}{2} \int \frac{1}{(x+3)^2} \ dx $$

L'ultimo integrale è una potenza -(x+3)^-1

$$ \int \frac{2x+5}{(x+1) \cdot (x+3)^2 } \ dx = \frac{3}{4} \cdot \log |x+1| - \frac{3}{4} \log | x+3| - \frac{1}{2} (x+3)^{-1} +C $$

Nota. L'ultimo integrale è l'integrale di una potenza perché $$ D [ - (x+3)^{-1} ] = - ( - 1) (x+3)^{-1-1} \cdot D[x+3] = 1 \cdot (x+3)^{-2} \cdot 1 = (x+3)^{-2} = \frac{1}{(x+3)^2} $$ Pertanto $$ \int \frac{1}{(x+3)^2} \ dx = - (x+3)^{-1} $$

Ho così risolto l'integrale.

$$ \int \frac{2x+5}{(x+1) \cdot (x+3)^2 } \ dx = \frac{3}{4} \cdot \log |x+1| - \frac{3}{4} \log | x+3| - \frac{1}{2} (x+3)^{-1} +C $$

C] Il polinomio al denominatore ha radici complesse

Devo risolvere l'integrale

$$ \int \frac{x-1}{x(x^2+1)} \ dx $$

Il polinomio al denominatore ha una radice reale x=0 e una radice complessa perché x²+1=0 non ha soluzioni reali.

In questo caso devo considerare un fratto semplice del tipo A/x nei numeri reale e un fratto semplice del tipo (Bx+C)/(x²+1) nei numeri complessi.

$$ \int \frac{x-1}{x(x^2+1)} \ dx = \int \frac{A}{x} + \frac{Bx+C}{x^2+1} \ dx $$

Per trovare i valori di A,B,C calcolo tutti i termini a denominatore comune nel secondo membro dell'equazione

$$ \int \frac{x-1}{x(x^2+1)} \ dx = \int \frac{A(x^2+1)+x(Bx+C)}{x(x^2+1)}\ dx $$

$$ \int \frac{x-1}{x(x^2+1)} \ dx = \int \frac{Ax^2+A+Bx^2+Cx}{x(x^2+1)}\ dx $$

$$ \int \frac{x-1}{x(x^2+1)} \ dx = \int \frac{x^2(A+B)+Cx+A}{x(x^2+1)}\ dx $$

I due membri dell'equazione hanno lo stesso denominatore.

Quindi, posso confrontare i polinomi al numeratore applicando il principio di identità dei polinomi ottenendo A+B=0, C=1, A=-1.

Scrivo le tre equazioni in un unico sistema per ottenere i valori di A,B,C

$$ \begin{cases} A+B=0 \\ C=1 \\ A=-1 \end{cases} $$

$$ \begin{cases} (-1)+B=0 \\ C=1 \\ A=-1 \end{cases} $$

$$ \begin{cases} B=1 \\ C=1 \\ A=-1 \end{cases} $$

Una volta trovati i valori delle costanti A=-1, B=1, C=1 li sostituisco nell'integrale

$$ \int \frac{x-1}{x(x^2+1)} \ dx = \int \frac{A}{x} + \frac{Bx+C}{x^2+1} \ dx $$

$$ \int \frac{x-1}{x(x^2+1)} \ dx = \int \frac{-1}{x} + \frac{(1)x+(1)}{x^2+1} \ dx $$

$$ \int \frac{x-1}{x(x^2+1)} \ dx = \int - \frac{1}{x} + \frac{x+1}{x^2+1} \ dx $$

Per la proprietà lineare l'integrale di una somma equivale alla somma di integrali

$$ \int \frac{x-1}{x(x^2+1)} \ dx = \int - \frac{1}{x} \ dx + \int \frac{x+1}{x^2+1} \ dx $$

$$ \int \frac{x-1}{x(x^2+1)} \ dx = - \int \frac{1}{x} \ dx + \int \frac{x+1}{x^2+1} \ dx $$

Ora gli integrali nel membro di sinistra dell'equazione sono facilmente risolvibili

Il primo integrale è un logaritmo ∫1/x dx=log|x|+C

$$ \int \frac{x-1}{x(x^2+1)} \ dx = - \log|x| + C + \int \frac{x+1}{x^2+1} \ dx $$

Anche il secondo integrale è facilmente risolvibile perché posso scomporre algebrcamente la funzione integranda in due fratti

$$ \int \frac{x-1}{x(x^2+1)} \ dx = - \log|x| + C + \int \frac{x}{x^2+1} + \frac{1}{x^2+1} \ dx $$

Questo mi permette di applicare la proprietà lineare degli integrali

$$ \int \frac{x-1}{x(x^2+1)} \ dx = - \log|x| + C + \int \frac{x}{x^2+1} \ dx + \int \frac{1}{x^2+1} \ dx $$

L'integrale di ∫x/(x^2+1) dx=1/2 log(x²+1)+C

$$ \int \frac{x-1}{x(x^2+1)} \ dx = - \log|x| + \log \frac{1}{2} \log (x^2+1) + C + \int \frac{1}{x^2+1} \ dx $$

Nota. La derivata di $$ D[ \log (x^2+1) ] = \frac{1}{x^2+1} \cdot D[x^2+1] = \frac{2x}{x^2+1} $$ Pertanto, mi basta moltiplicare log(x^2+1) per 1/2 e ottengo l'integrale che m interessa trovare. $$ D[ \frac{1}{2} \cdot \log (x^2+1) ] = \frac{1}{2} \cdot \frac{1}{x^2+1} \cdot D[x^2+1] = \frac{1}{2} \cdot \frac{2x}{x^2+1} = \frac{x}{x^2+x} $$

Infine, l'integrale di ∫1/(x²+1) dx=arctan(x)+C

$$ \int \frac{x-1}{x(x^2+1)} \ dx = - \log|x| + \log \frac{1}{2} \log (x^2+1) + \arctan(x) + C $$

L'integrale è risolto.

E così via.