Rombo

Il rombo è un parallelogramma con tutti i lati congruenti.

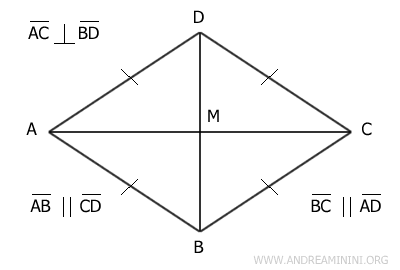
In pratica, il rombo è un quadrilatero con quattro lati di uguale lunghezza.

Essendo un parallelogramma, il rombo eredita tutte le proprietà dei parallelogrammi:

• I lati opposti sono paralleli.
• Gli angoli e i lati opposti sono congruenti.
• Gli angoli adiacenti a un lato sono supplementari.
• Le diagonali si intersecano nel loro punto medio.

A queste aggiunge alcune caratteristiche peculiari del rombo.

• I lati del rombo sono congruenti
• Le diagonali sono perpendicolari, ossia formano un angolo di 90°.
• Le diagonali sono le bisettrici degli angoli

Prese singolarmente queste condizioni sono necessarie ma non sufficienti per stabilire che un quadrilatero sia un rombo.

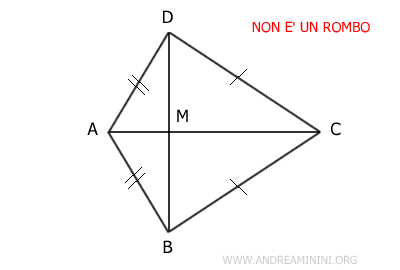
Ad esempio, un quadrilatero può avere le diagonali perpendicolari senza essere un rombo (es. il deltoide convesso o aquilone o kite). E' necessario che il quadrilatero sia anche un parallelogramma.

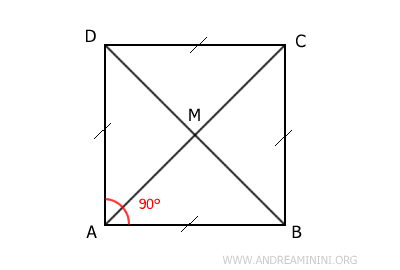
Inoltre, il quadrato possiede tutte le proprietà dei rombi, ma si distingue per avere angoli retti di 90°. Pertanto, si può considerare il quadrato come un particolare tipo di rombo. Tuttavia, nella pratica, quando mi imbatto in una figura con queste caratteristiche, tendo a chiamarla 'quadrato'.

Le formule del rombo

Ecco alcune formule utili per calcolare gli elementi geometrici di un rombo

• Perimetro
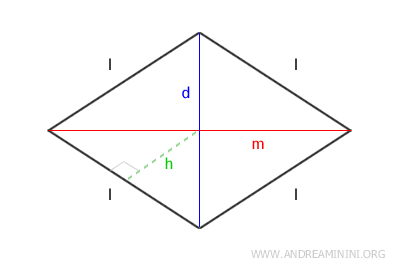
  Il perimetro del rombo è uguale a 4 volte il lato. $$ P = 4 \cdot l $$
• Area
  L'area del rombo è uguale al prodotto della diagonale maggiore (d) per la diagonale minore (m) diviso due. $$ A = \frac{d \cdot m}{2} $$ In alternativa, essendo il rombo un parallelogramma, posso calcolare l'area moltiplicando il lato (l) per l'altezza (h). $$ A = l \cdot h $$
• Lato
  La lunghezza di un lato si ottiene utilizzando il teorema di Pitagora. $$ l = \sqrt{ ( \frac{d}{2})^2 + ( \frac{m}{2})^2 } $$
• La diagonale maggiore
  La formula per calcolare la diagonale maggiore la ricavo da quella del lato. $$ d = 2 \cdot \sqrt{ l^2 - (\frac{m}{2})^2 } $$
• La diagonale minore
  Anche la formula per calcolare la diagonale minore la ricavo da quella del lato. $$ m = 2 \cdot \sqrt{ l^2 - (\frac{d}{2})^2 } $$

  Spiegazione. I passaggi algebrici per ottenere le formule della diagonale maggiore e minore del rombo sono molto semplici. Tuttavia, per completezza li scrivo qui sotto. Ad ese≅mpio, per calcolare la diagonale maggiore parto dalla formula del lato. $$ l = \sqrt{ ( \frac{d}{2})^2 + ( \frac{m}{2})^2 } $$ Faccio uscire il termine (d/l)² dalla radice quadrata. $$ l = \frac{d}{2} + \sqrt{ ( \frac{m}{2})^2 } $$ Ricavo la diagonale maggiore $$ - \frac{d}{2} = -l + \sqrt{ ( \frac{m}{2})^2 } $$ Applico la proprietà invariantiva delle equazioni e moltiplico entrambi i membri per -1 $$ - \frac{d}{2} \cdot (-1) = [ -l + \sqrt{ ( \frac{m}{2})^2 } ] \cdot (-1) $$ $$ \frac{d}{2} = l - \sqrt{ ( \frac{m}{2})^2 } $$ Porto il termine l (lato) dentro la radice $$ \frac{d}{2} = \sqrt{ l^2 - ( \frac{m}{2})^2 } $$ Applico nuovamente la proprietà invariantiva e moltiplico per due entrambi i membri dell'equazione $$ 2 \cdot \frac{d}{2} = 2 \cdot \sqrt{ l^2 - ( \frac{m}{2})^2 } $$ Il risultato finale è la formula della diagonale maggiore $$ d = 2 \cdot \sqrt{ l^2 - ( \frac{m}{2})^2 } $$ La stessa procedura posso ripeterla per ottenere la formula della diagonale minore. $$ m = 2 \cdot \sqrt{ l^2 - (\frac{d}{2})^2 } $$

Come disegnare un rombo

Supponiamo di voler disegnare un rombo con una diagonale principale di 6 unità e una seconda diagonale di 4 unità.

Inizio tracciando un segmento AB di 6 unità, che rappresenterà la diagonale principale del rombo.

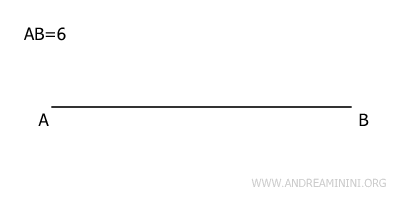
Poi trovo una retta perpendicolare al segmento AB.

Con un'apertura del compasso a piacere e leggermente superiore alla metà di AB, centro la punta del compasso sul punto A e traccio un arco.

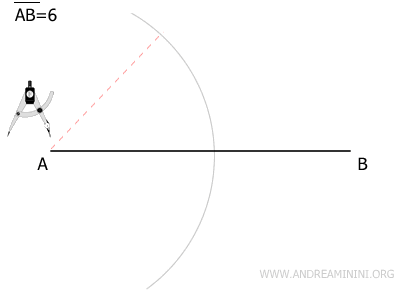
Senza cambiare l'apertura del compasso, centro il compasso sul punto B e traccio un altro arco che interseca il primo in due punti distinti.

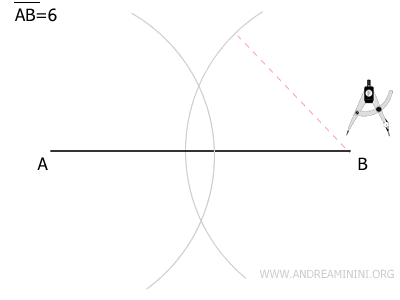
Disegno una retta attraverso i due punti di intersezione degli archi. Questa retta è perpendicolare al segmento AB.

Il punto dove la retta perpendicolare interseca AB è il punto medio M della diagonale principale del rombo.

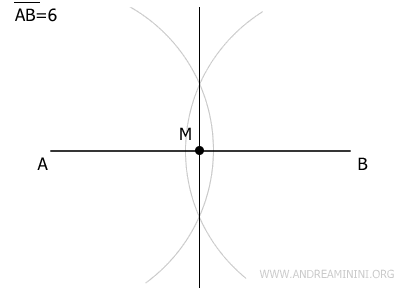
A questo punto traccio la seconda diagonale del rombo.

Centro il compasso sul punto M e traccio un arco con un raggio di metà della lunghezza della seconda diagonale, ovvero 2 unità.

I punti dove l'arco interseca la retta perpendicolare sono gli estremi C e D della seconda diagonale.

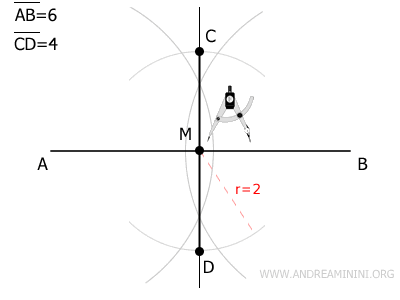
Infine, connetto i punti A, B, C e D per formare il rombo, tracciando i segmenti AC, AD, BC e BD.

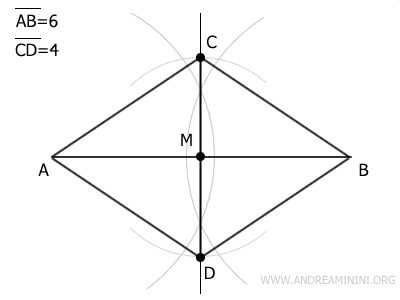
Seguendo questi passaggi, ottengo un rombo, ossia un parallelogramma con lati congruenti, diagonali perpendicolari, una diagonale principale di 6 unità e una seconda diagonale di 4 unità.

Osservazioni

Alcune osservazioni e note a margine sul rombo

• Un parallelogramma è un rombo se ha due lati consecutivi congruenti

  Dimostrazione. Poiché ABCD è un parallelogramma, sappiamo che i lati opposti sono congruenti. Quindi, AB≅CD e AD≅BC. Se per ipotesi i lati consecutivi AB e BC sono congruenti AB≅BC posso dedurre per la proprietà transitiva che AB≅AD e BC≅CD. Quindi, tutti i lati del parallelogramma sono congruenti, il che significa che ABCD è un rombo.

• Le diagonali del rombo sono perpendicolari tra loro e bisettrici degli angoli
  

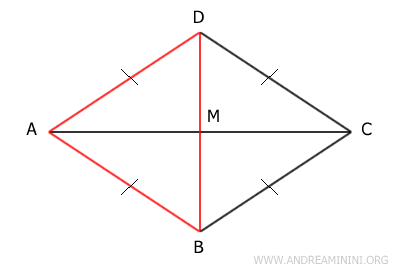
  Dimostrazione. Considero un rombo ABCD in cui le diagonali si incontrano nel loro punto medio M. Devo dimostrare che le diagonali AC e BD sono perpendicolari tra loro e bisettrici dei rispettivi angoli.
  
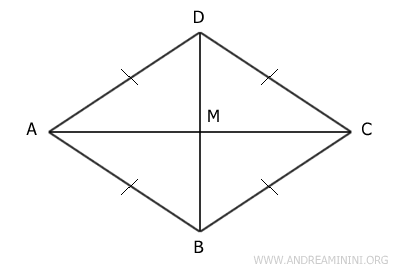
  Poiché è un rombo, ha tutti i lati congruenti, ossia della stessa lunghezza. Quindi, il triangolo ACD è un triangolo isoscele perché i lati AD≅CD sono congruenti. Nei triangoli isoscele la mediana è anche l'altezza e la bisettrice dell'angolo al vertice. Quindi, il segmento DM è la bisettrice dell'angolo al vertice D. Inoltre, il segmento DM è anche l'altezza. Sapendo che l'altezza del triangolo è perpendicolare al lato opposto, deduco che il segmento DM è perpendicolare al segmento AC (diagonale del rombo). Lo stesso discorso vale per il triangolo ABC perché, per il terzo criterio di congruenza (LLL), è congruente con il triangolo ACD ossia ABC≅ACD. Pertanto la diagonale BD è perpendicolare alla diagonale AB (e viceversa) ed è bisettrice degli angoli ai vertici B e D.
  
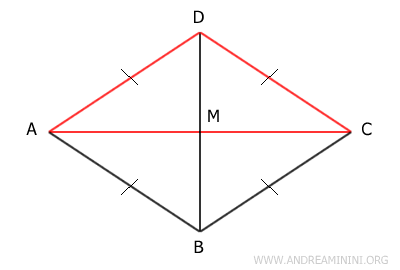
  Ora considero il triangolo ABD. Anche in questo caso si tratta di un triangolo isoscele perché i lati AD≅AB sono congruenti. Pertanto, il segmento AM è la mediana, l'altezza e la bisettrice dell'angolo al vertice A. Da ciò deduco che è bisettrice dell'angolo al vertice A ed è perpendicolare alla diagonale BD. Lo stesso discorso si ripete per il triangolo BCD perché, per il terzo criterio di congruenza, è congruente con il triangolo ACD ossia BCD≅ABD. In conclusione, la diagonale AB è bisettrice degli angoli ai vertici A e B ed è perpendicolare alla diagonale BD.
  

• Un parallelogramma è un rombo se ha le diagonali perpendicolari

  Dimostrazione. Supponiamo inizialmente che ABCD sia un parallelogramma e che le sue diagonali AC e BD siano perpendicolari tra loro. Poiché ABCD è un parallelogramma, le sue diagonali si dividono a metà nel loro punto di medio M. Pertanto, AM è congruente a CM e BM è congruente a DM.
  
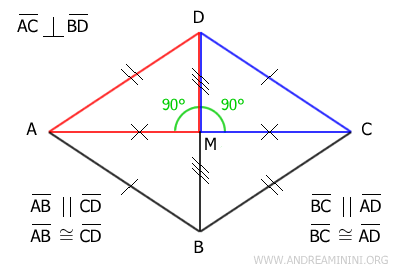
  Sapendo che AM≅CM e BM≅DM, i triangoli rettangoli AMD e CMD sono congruenti (AMD≅CMD) per il primo criterio di congruenza, dato che hanno un lato in comune (DM), i lati congruenti AM≅CM e l'angolo retto congruente. Essendo due triangoli congruenti, tutti i loro lati e angoli sono congruenti. In particolar modo mi interessa sapere che le loro ipotenuse sono congruenti AD≅CD perché sono due lati consecutivi del parallelogramma. Da questo deduco che tutti i lati del parallelogramma sono congruenti, perché un parallelogramma ha i lati opposti congruenti. Quindi, il parallelogramma è un rombo.

• Un parallelogramma è un rombo se una diagonale è la bisettrice dell'angolo
  

  Dimostrazione. Considero un parallelogramma ABCD. Per ipotesi una diagonale del parallelogramma è anche una bisettrice. Ad esempio, la diagonale AC è una bisettrice dell'angolo al vertice A. Quindi, gli angoli α'≅α'' sono congruenti.
  
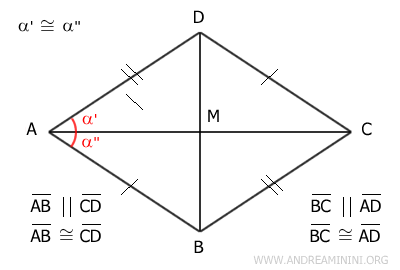
  I lati opposti di un parallelogramma sono sempre paralleli, quindi la diagonale AC posso considerarla come la trasversale delle rette parallele AD||BC. Per il teorema delle rette parallele gli angoli alterni interni sono congruenti. Di conseguenza, gli angoli α' e γ sono congruenti (α'≅γ).
  
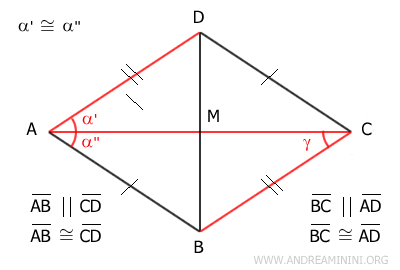
  Questo vuol dire che il triangolo ABC ha due angoli congruenti (α'≅γ) adiacenti al lato AC, quindi ABC è un triangolo isoscele rispetto alla base AC. Essendo un triangolo isoscele i suoi lati obliqui AB≅BC sono congruenti. Da questo deduco che il parallelogramma è un rombo, perché due lati consecutivi AB e BC sono congruenti.

• Una diagonale divide il rombo in due triangoli isosceli congruenti

  Dimostrazione. Il rombo ha tutti i lati congruenti e le diagonali perpendicolari. Inoltre, essendo un parallelogramma, le diagonali si incontrano nel loro punto medio M. Quindi, ogni diagonale divide il rombo in due triangoli isosceli. Ad esempio, la diagonale AC divide il rombo ABCD nei triangoli ACD e ABC. Questi triangoli hanno due lati obliqui congruenti AD≅CD e AB≅BC. Pertanto, sono due triangoli isosceli. Inoltre, per il 3° criterio di congruenza (LLL) sono triangoli congruenti ACD≅ABC perché hanno tutti i lati congruenti.
  
  Anche l'altra diagonale BD divide il rombo in due triangoli ABD e BCD. I lati obliqui AB≅AD e BC≅CD sono congruenti. Quindi, entrambi i triangoli sono isosceli. Inoltre, avendo tutti e tre i lati congruenti, per il terzo criterio di congruenza (LLL) sono due triangoli congruenti ABD≅BCD.
  

• Le diagonali dividono il rombo in quattro triangoli rettangolo congruenti

  Dimostrazione. Il rombo ha tutti i lati congruenti e le diagonali sono perpendicolari fra loro. Inoltre, le perpendicolari si incontrano nel loro punto medio M. Pertanto, per il terzo criterio di congruenza (LLL) i triangoli AMD≅CDM sono congruenti perché hanno tutti i lati congruenti. Per la stessa ragione sono congruenti i triangoli ABM≅BCM sono congruenti.
  
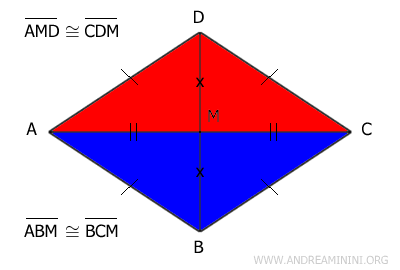
  Anche i triangoli AMD≅ABM sono congruenti perché hanno tre lati congruenti. Quindi, per la proprietà transitiva tutti i triangoli rettangolo sono congruenti fra loro AMD≅ABM≅BCM≅CDM.
  

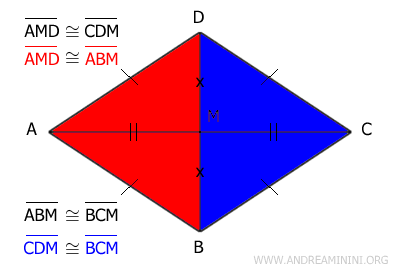
E così via.