Il teorema della somma degli angoli esterni di un poligono convesso

In un poligono convesso di n lati, la somma degli angoli esterni (uno per ogni vertice) è sempre congruente a un angolo giro (360°).

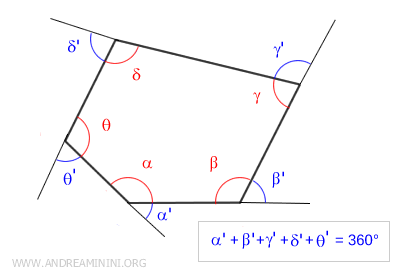
In altre parole, la somma degli angoli esterni in un poligono convesso è indipendente dal numero dei lati e dalla forma ovvero è un invariante.

Ad esempio, in un triangolo, quadrato, pentagono o poligono qualsiasi con n lati, la somma degli angoli esterni è sempre 360°.

Esempio. Devo camminare lungo il bordo di un recinto. Non importa la forma esatta del recinto: potrebbe avere molti angoli o solo pochi. Deve però essere un poligono convesso. Ogni volta che raggiungo un angolo del recinto, devo cambiare direzione.

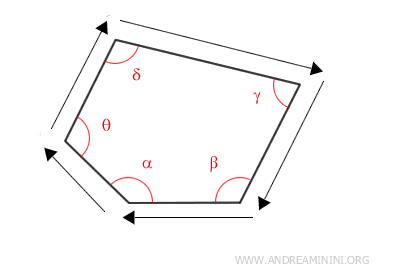
La somma di tutti questi cambiamenti di direzione mentre cammino intorno al recinto è uguale a 360°, proprio come se avessi fatto un giro completo in cerchio intorno al recinto.

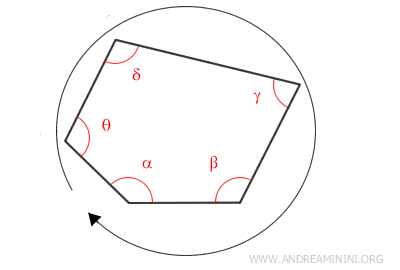
La dimostrazione

Considero un poligono convesso qualsiasi.

Ad esempio, un poligono convesso con n=5 lati.

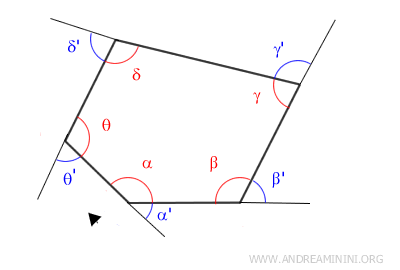
Ogni angolo esterno del poligono convesso è adiacente all'angolo interno.

Pertanto, ogni angolo interno è complementare all'angolo interno, con cui forma un angolo piatto di 180°.

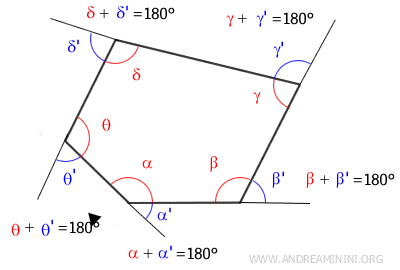
Questo vuol dire che in un poligono convesso con n lati ci sono n angoli e la somma degli angoli interni ed esterni è pari a n·180°

$$ n \cdot 180° $$

Sapendo che la somma degli angoli interni è uguale a (n-2)·180, posso calcolare la somma degli angoli esterni per differenza.

In pratica, la somma degli angoli esterni è uguale alla somma angoli interni ed esterni meno la somma degli angoli interni.

Quindi, la somma degli angoli esterni del poligono convesso è la seguente:

$$ n \cdot 180° - [ (n-2) \cdot 180° ] $$

Con qualche semplice passaggio algebrico ottengo

$$ [ n - (n-2) ] \cdot 180° = $$

$$ ( n - n + 2 ) \cdot 180° = $$

$$ 2 \cdot 180° = 360° $$

Quindi, indipendentemente dal numero dei lati, la somma degli angoli esterni di un poligono con n lati è sempre pari a un angolo giro ossia 360°.

Note

Alcune osservazioni e note sulla somma degli angoli esterni di un poligono convesso.

• La somma degli angoli esterni è un invariante più forte della somma degli angoli interni
  La somma delle ampiezze degli angoli esterni di un poligono convesso è uguale a 360° per qualsiasi poligono convesso, prendendo un angolo esterno per ciascun vertice, indipendentemente dal numero dei lati e dalla forma. La somma degli angoli interni di un poligono convesso, invece, dipende dal numero dei lati $ n $ del poligono convesso ed è pari a $ (n-2) \cdot 180° $. Pertanto, è un invariante meno forte perché varia al variare di $ n $.

E così via.