La riduzione dei lati nei poligoni convessi
Un poligono convesso è sempre equivalente a un poligono con numero inferiore di lati che ha la stessa area.
Il principio si basa sul fatto che posso ridurre il numero di lati di un poligono attraverso la scomposizione e il riarrangiamento.
Fa ovviamente eccezione alla regola il triangolo, in quanto non esiste un poligono con due lati. Un poligono, per definizione, ha almeno tre lati.
Questo concetto è particolarmente utile per dimostrare come, nella geometria piana, il cambiamento della forma non modifica l'area di un poligono.
Nota. Si può applicare sia ai poligoni convessi che concavi. Tuttavia, è molto più semplice e intuitivo per i poligoni convessi. Nei poligoni concavi, il processo potrebbe richiedere tagli e riarrangiamenti più complicati per gestire le indentazioni.
Come costruire un poligono equivalente con un lato in meno
Esistono diversi modi per ridurre il numero dei lati.
Ad esempio, scomporre il poligono in poligoni più piccoli e ricomporlo in una forma diversa.
Uno dei processi più semplici si basa sulle diagonali del poligono.
Ad esempio, considero un poligono qualsiasi (regolare o irregolare). In questo caso si tratta di un esagono.
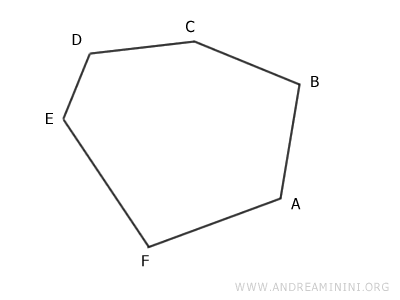
Traccio la diagonale tra due punti che hanno un punto intermedio.
Ad esempio, la retta diagonale tra A e C che hanno B come punto intermedio.
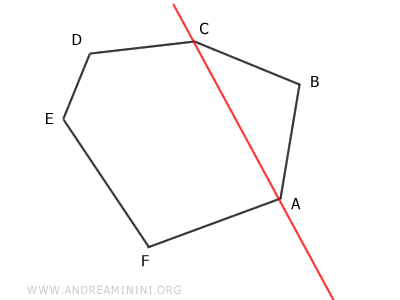
Traslo la retta diagonale facendola passare sul punto intermedio B.
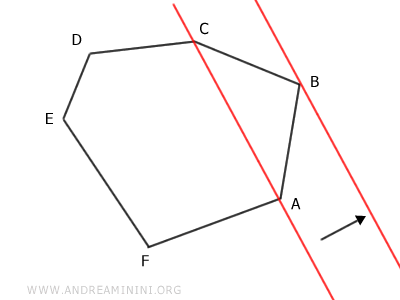
Infine, prolungo uno dei segmenti che ha per estremo A oppure C fino a intersecare la retta.
Ad esempio, prolungo il segmento AF fino al punto A'.
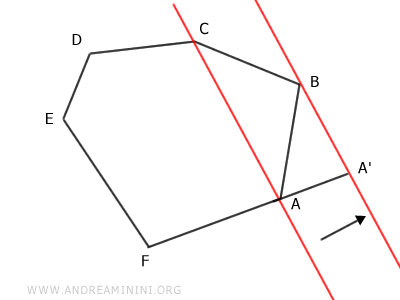
Infine, traccio un segmento A'C che congiunge il punto A' con il punto C eliminando il vertice B del poligono.
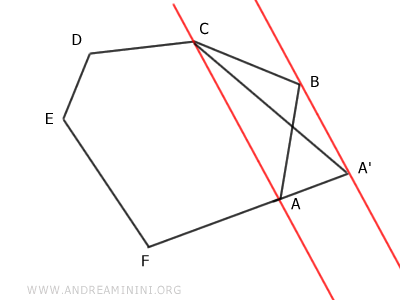
Il risultato finale è un poligono A'CDEF con cinque lati ossia un pentagono.
Il pentagono appena ottenuto è equivalente all'esagono iniziale, ovvero ha la stessa area.
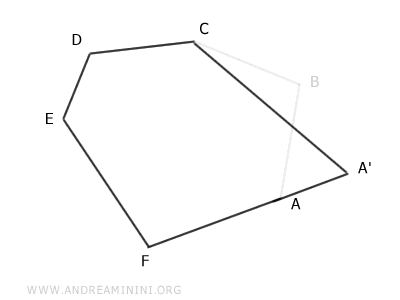
Dimostrazione. Per dimostrarlo basta osservare i triangoli AA'C e ABC.
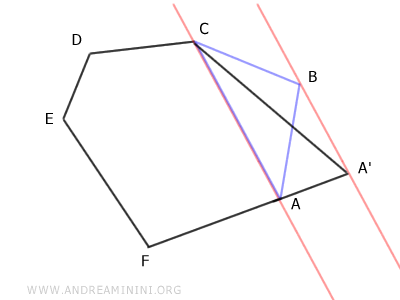
Questi due triangoli hanno la stessa base (AC) e la stessa altezza (AA'≅BB'). Quindi, secondo il teorema di congruenza dei triangoli, sono due triangoli equivalenti ovvero hanno la stessa area.
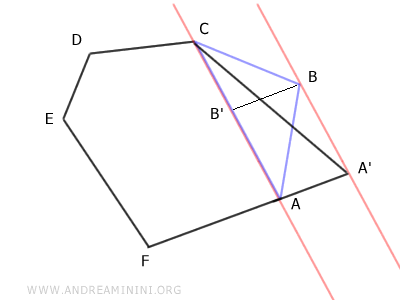
A questo punto basta osservare che l'esagono è composto dal poligono ACDEF sommato al triangolo ABC. $$ ABCDEF \doteq ACDEF + ABC $$ Il pentagono A'CDEF è composto dal poligono ACDEF sommato al triangolo AA'C. $$ A'CDEF \doteq ACDEF + AA'C $$ Sapendo che i triangoli ABC e AA'C sono equivalenti, si comprende che sia l'esagono che il pentagono sono poligoni equicomposti ossia composti dagli stessi poligoni equivalenti. $$ ABCDEF \doteq ACDEF + ABC \doteq ACDEF + AA'C \doteq A'CDEF $$ $$ ABCDEF \doteq A'CDEF $$ Pertanto, l'esagono ABCDEF e il pentagono A'CDEF sono equivalenti.
Reiterando il processo posso ridurre ulteriormente il pentagono A'CDEF in un quadrilatero C'DEF (4 lati) equivalente.
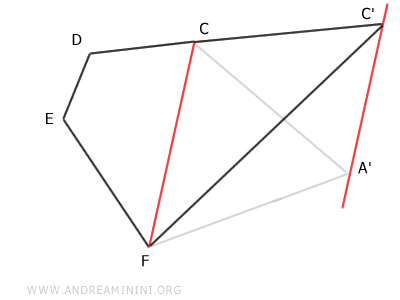
Infine, posso ridurre il quadrilatero C'DEF in un triangolo C'D'F (3 lati) equivalente.
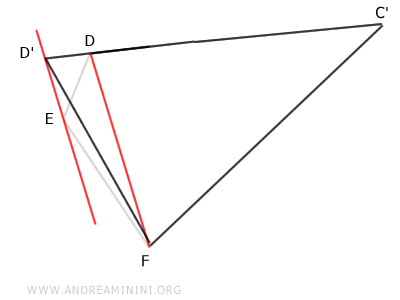
Da questo deduco che ogni poligono convesso può essere ridotto a un triangolo equivalente.
Nota. Il metodo che ho descritto per ridurre il numero dei lati tramite le diagonali non è un metodo standard nella geometria euclidea. Nella pratica, cambiare il numero di lati di un poligono mantenendo la stessa area richiede tecniche di scomposizione e riarrangiamento che non sono così dirette come il semplice tracciamento o spostamento di diagonali.
Osservazioni
Alcune osservazioni e note a margine
- Poligoni concavi
Nel caso dei poligoni concavi la riduzione del numero dei lati mantenendo l'area non è sempre possibile nella geometria euclidea.
E così via.
