Il teorema della somma degli angoli interni di un poligono convesso
In un poligono convesso di n lati, la somma degli angoli interni è congruente a n-2 angoli piatti (180°). $$ (n-2) \cdot 180° $$
La somma degli angoli interni di un poligono convesso dipende dal numero dei lati del poligono.
Ad esempio, un triangolo è composto da n=3 lati.
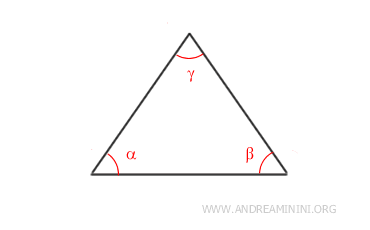
Quindi, la somma degli angoli interni di un triangolo è pari a 180°.
$$ (n-2) \cdot 180° $$
$$ (3-2) \cdot 180° = 180° $$
Un rettangolo, invece, è composto da n=4 lati.
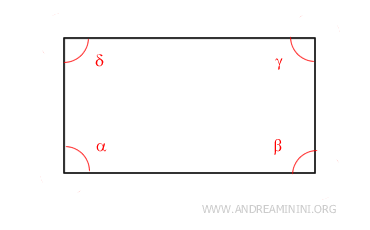
In questo caso la somma degli angoli interni di un rettangolo è uguale a 360°.
$$ (n-2) \cdot 180° $$
$$ (4-2) \cdot 180° $$
$$ 2 \cdot 180° = 360° $$
Un pentagono è composto da n=5 lati.
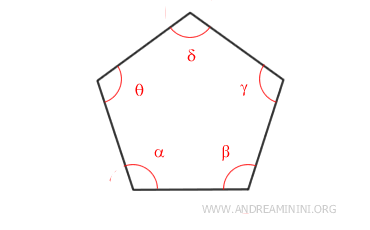
Quindi, la somma degli angoli interni è pari a 540°
$$ (n-2) \cdot 180° $$
$$ (5-2) \cdot 180° $$
$$ 3 \cdot 180° = 540° $$
E via dicendo gli altri poligoni.
La dimostrazione
La dimostrazione è molto semplice.
Considero un poligono convesso qualsiasi con n lati, ad esempio un poligono con n=5 lati.
Può essere un poligono regolare o irregolare. Non importa. Ciò che conta è che sia convesso.
Prendo un punto interno $ P $ qualsiasi e lo congiungo con i vertici del poligono.
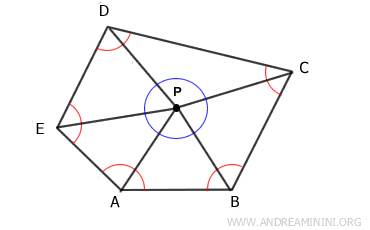
In questo modo suddivido il poligono in $ n $ triangoli.
Sapendo che la somma degli angoli interni di un triangolo è pari a 180°, la somma degli angoli interni del poligono a $ n $ lati è pari alla somma delle ampiezze degli angoli interni degli $ n $ triangoli, meno la somma degli angoli intorno al punto $ P $che è uguale a 360°.
$$ n \cdot 180 ° - 360° $$
Con qualche passaggio algebrico ottengo
$$ n \cdot 180 ° - 2 \cdot 180° $$
$$ (n-2) \cdot 180° $$
Questo dimostra la formula iniziale.
Nota. In questo caso, essendoci $ n =5 $ lati, la somma degli angoli interni di un poligono convesso con 5 lati è pari a 540°. $$ (5-2) \cdot 180° = 3 \cdot 180° = 540° $$
Dimostrazione alternativa
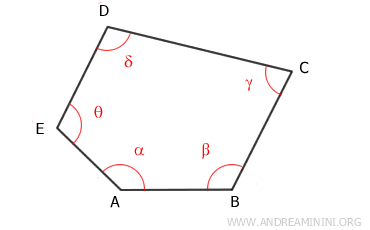
Considero un poligono convesso con n lati, ad esempio un poligono con n=5 lati.

Seleziono un vertice a caso e traccio tutte le diagonali a partire da questo vertice.
Ad esempio, scelgo il vertice A.
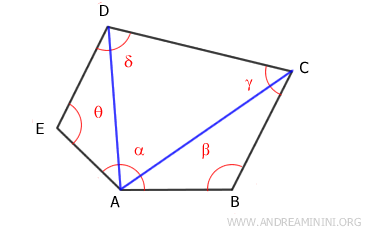
Da un vertice del poligono posso tracciare n-3 diagonali che suddividono la figura geometrica in n-2 triangoli.
In questo caso, scompongo la figura convessa in tre triangoli: ADE, ACD, ABC.
$$ n - 2 = 5 - 2 = 3 \ \text{triangoli} $$
In questo modo suddivido il problema iniziale della somma degli angoli interni del poligono convesso in sottoproblemi più semplici da risolvere.
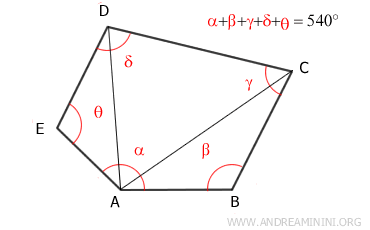
Sapendo che la somma degli angoli interni di un triangolo è pari a 180° e che il poligono convesso è scomposto in tre triangoli, deduco che la somma degli angoli interni del poligono convesso è uguale a 180° per tre.
$$ 180° \cdot 3 = 540° $$
In questo caso, la somma degli angoli interni di un poligono convesso con 5 lati è pari a 540°.
E così via.
