Poligoni equicomposti

Due o più poligoni sono detti poligoni equicomposti o equiscomponibili quando sono la somma di poligoni congruenti.

In altre parole, due poligoni sono equicomposti se posso suddividerli in un eguale numero finito di parti (poligoni più piccoli) e ciascuna parte di una figura è congruente a una delle parti dell'altra figura, e viceversa.

Questo mi permette di riarrangiare le parti di una figura per formare l'altra figura.

Ad esempio, se ho due poligoni (figura 1 e figura 2) e posso scomporre il primo in parti che possono essere riassemblate per formare il secondo poligono, e viceversa, allora sono poligoni equicomposti.

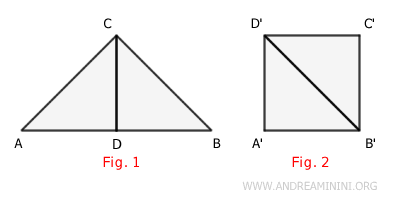
Nota. Questo concetto è strettamente legato al principio di Cavalieri, che afferma che se due figure solide nello spazio tridimensionale sono disposte in modo tale che, in ogni piano parallelo a un piano fisso, le sezioni di ciascuna figura hanno la stessa area, allora le due figure hanno lo stesso volume.

Un esempio pratico

Considero due poligoni: la figura 1 e la figura 2.

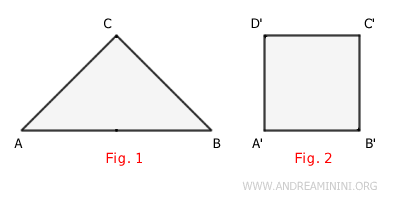
Scompongo il poligono della figura 1 in due parti, ognuna delle quali è un poligono più piccolo (ACD e BCD).

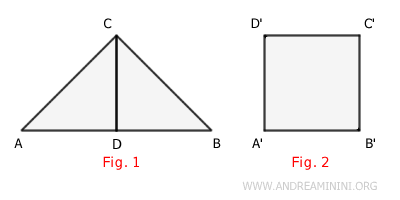
La somma delle aree dei poligoni componenti è uguale all'area del poligono A che li contiene.

$$ Area(ABC) = Area(ACD) + Area(BCD) $$

Riassemblo le due parti in modo diverso, senza sovrapporle, fino a coprire esattamente la superficie del poligono B.

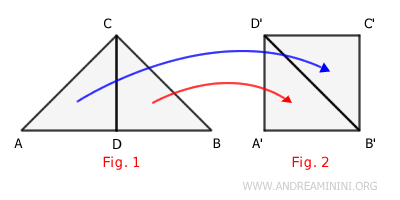
Da questo deduco che i due poligoni A e B sono scomponibili negli stessi poligoni congruenti e, quindi, hanno la stessa superficie (superfici equivalenti) ossia coprono lo stesso spazio.

$$ ACD \cong B'C'D' $$ $$ BCD \cong A'B'D' $$

In pratica sono composti dalla stessa partizione di poligoni.

Poiché hanno la stessa estensione di superficie, hanno la stessa area che a sua volta è la somma delle aree dei poligoni componenti.

In questo caso sono detti equicomposti.

Osservazioni

Alcune note a margine sui poligoni equicomposti

• Due poligoni sono equicomposti anche se sono la differenza di poligoni congruenti
  Valgono le stesse considerazioni fatte per la somma di poligoni congruenti.
• Due poligoni equicomposti hanno la stessa area, ovvero hanno la superficie equivalente
  Per questa ragione sono anche detti poligoni equivalenti.
• L'equiscomponibilità è una relazione di equivalenza
  Quindi, valgono le stesse proprietà matematiche soddisfatte dalle relazioni di equivalenza. Le superfici con la stessa area appartengono alla stessa classe di equivalenza.
• Due poligoni equicomposti sono poligoni equivalenti
  Quando due poligoni sono composti dalle stesse parti, allora sono poligoni equivalenti perché hanno la stessa area.
• Teorema di Dehn
  Due figure equiscomponibili sono anche geometricamente equivalenti, ma non si può affermare il contrario.

  Esempio. Nel piano due poligoni equivalenti hanno la stessa area e sono composti dalle stesse superfici equivalenti, quindi sono sempre equiscomponibili. Viceversa, nello spazio due poliedri con lo stesso volume non è detto che siano anche equiscomponibili.

• Il concetto di equicomposizione nella storia della geometria e della matematica
  Il concetto di equicomposizione ha importanti implicazioni nella teoria della misura, specialmente nel contesto dell'equivalenza delle figure geometriche in termini di area o volume, e nella comprensione e dimostrazione delle proprietà delle figure geometriche.

  Esempio. Basta citare come esempio il famoso problema del quadrato greco. Questo problema si occupa della possibilità di suddividere un quadrato in pezzi che possono essere riorganizzati per formare un cerchio di uguale area. E' una questione che ha portato nei secoli allo sviluppo della teoria della misura e del calcolo integrale moderno.

E così via.