Momento angolare
Il momento angolare è una grandezza fisica che descrive lo stato rotazionale di un corpo rispetto a un punto o a un asse. $$ \vec{L} = \vec{r} \times \vec{p} = \vec{r} \times (m \vec{v}) $$ Dove
- $\vec{r}$ = è il vettore posizione rispetto al punto o all'asse di rotazione scelto
- $\vec{p} = m \vec{v}$ = è la quantità di moto, cioè la massa $m$ del corpo per la velocità $ \vec{v} $
Il prodotto vettoriale $ \vec{r} \times \vec{p} $ restituisce un vettore perpendicolare al piano formato da $\vec{r}$ e $\vec{v}$.
Cosa influenza il momento angolare?
Il momento angolare dipende:
- dalla posizione del corpo $ \vec{r} $ rispetto al punto $ O $ scelto come riferimento
- dalla quantità di moto del corpo $ \vec{p} = m \vec{v} $
- dalla direzione del moto rispetto alla posizione
Ad esempio, in un moto circolare non uniforme,un corpo si muove lungo una traiettoria circolare con velocità tangenziale variabile.
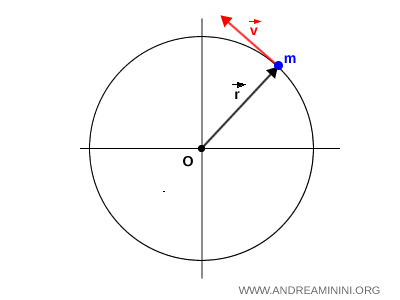
In questo caso la distanza $ r $ tra il corpo e il centro di rotazione $ O $ è costante. Se anche la massa $ m $ del corpo è costante, il momento angolare è direttamente proporzionale alla velocità tangenziale $ \vec{v} $.
Nota. È importante sottolineare che anche un corpo che si muove in linea retta può possedere momento angolare, a condizione che la sua traiettoria non attraversi il punto considerato $ O $, poiché durante il moto varia comunque il vettore posizione $\vec{r}$ rispetto al punto preso come riferimento.
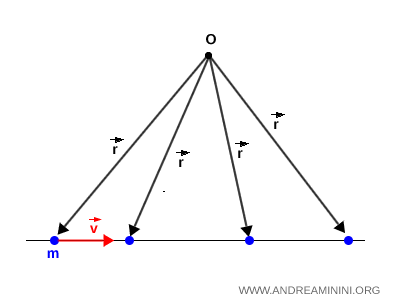
Nel caso particolare in cui il moto del corpo è lineare e passa per il punto preso come riferimento $ O $, il momento angolare è nullo a qualsiasi distanza.
Il modulo del momento angolare dipende dall'angolo $ \theta $ tra $ \vec{r} $ e $ \vec{v} $.
$$ L = mrv \cdot \sin \theta $$
Questo valore varia tra due estremi;
- Se l'angolo è $ \theta=90° $ il momento angolare è massimo $ L=mrv $ perché $ \vec{r} $ e $ \vec{v} $ sono perpendicolari.
- Se l'angolo è $ \theta=0° $ o $ \theta=180° $ il momento angolare è nullo $ L=0 $ perché $ \vec{r} $ e $ \vec{v} $ sono paralleli.
In generale, il momento angolare dipende dalla massa del corpo, dalla componente perpendicolare della sua posizione rispetto all'asse di rotazione, dalla sua velocità tangenziale e dal sistema di riferimento scelto.
Inoltre, il momento angolare cambia al variare della posizione del corpo rispetto al punto $ O $. Quindi, non è una proprietà del corpo.
Un esempio pratico
Considero un atleta che sta per eseguire un lancio del martello.
Il martello ha massa $m = 7{,}26\,\text{kg}$ ed è legato a una fune lunga $r = 1{,}20\,\text{m}$.
Durante la rotazione, il martello descrive un cerchio orizzontale attorno al punto di presa dell’atleta, che costituisce il centro di rotazione. In questa fase, l’atleta imprime al martello una velocità tangenziale crescente.
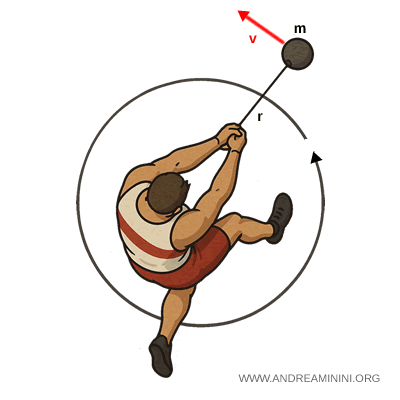
Al momento del rilascio, se la velocità tangenziale del martello è $v = 28{,}0\,\text{m/s}$, il momento angolare rispetto al centro di rotazione si calcola con la formula:
$$ L = m r v $$
Sostituisco i valori numerici dell'esempio.
$$ L = (7{,}26\,\text{kg}) \cdot (1{,}20\,\text{m}) \cdot (28{,}0\,\text{m/s}) $$
$$ L \approx 243{,}94\,\text{kg·m}^2/\text{s} $$
Quindi, al momento del rilascio il momento angolare è $ L \approx 243{,}94\,\text{kg·m}^2/\text{s} $.
Questo valore dipende da tre fattori:
- La massa del martello: più è pesante, maggiore è $L$.
- Il raggio: più è lungo il braccio della leva, maggiore è $L$.
- La velocità tangenziale: è il fattore decisivo, perché è quello che l’atleta modifica attivamente durante il lancio.
Se, ad esempio, l’atleta avesse rilasciato il martello a metà velocità, cioè a $v = 14{,}0\,\text{m/s}$, il momento angolare sarebbe stato più basso:
$$ L = 7{,}26 \cdot 1{,}20 \cdot 14{,}0 = 121{,}968 \approx 121{,}97\,\text{kg·m}^2/\text{s} $$
Questo vuol dire che per fermare o modificare il moto rotatorio rispetto al punto sarebbe necessaria una forza inferiore.
Nota. Nel caso del lancio del martello la massa del peso $ m $ e il raggio $ r $ sono costanti. In questo caso, il momento angolare è direttamente proporzionale alla velocità tangenziale $ v $. Quindi: più il martello gira veloce, più è difficile fermarlo. Tuttavia, in un’analisi più accurata, occorre tenere conto anche delle variazioni del raggio dovute ai movimenti dell’atleta e alla lunghezza del suo braccio, che modificano direttamente $ r $ e, di conseguenza, anche il momento angolare.
Conservazione del momento angolare
Se su un sistema non agiscono forze esterne con momento torcente (cioè che tendano a farlo ruotare), il suo momento angolare totale si conserva.
Questo principio spiega molti fenomeni fisici.
Ad esempio, perché un pattinatore che avvicina le braccia ruota più velocemente o perché i satelliti e i pianeti seguono traiettorie stabili.
Il momento angolare della Terra
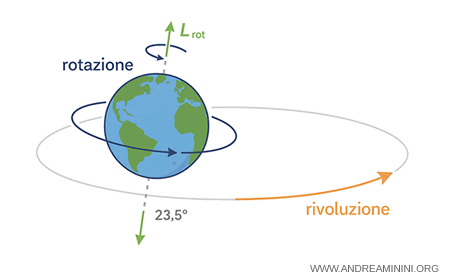
La Terra possiede due momenti angolari distinti, perché compie due movimenti diversi:
- Momento angolare di rotazione
Un momento angolare di rotazione legato al moto di rotazione sul proprio asse, che la Terra compie in circa 24 ore. In questo caso, il momento angolare dipende dalla massa della Terra, il suo raggio e la distribuzione della massa e la velocità angolare di rotazione $ \omega $. Questo momento angolare è responsabile, ad esempio, della conservazione dell’asse terrestre e quindi dell’alternarsi del giorno e della notte.Nota. Per un corpo rigido il momento angolare di rotazione è $$ L_{\text{rot}} = I \omega $$ Dove $ I $ è il momento d’inerzia della Terra e $ \omega $ è la velocità angolare di rotazione. Per una sfera leggermente schiacciata come la Terra, in prima approssimazione: $$ I \approx \frac{2}{5} M R^2 $$ e $$ \omega = \frac{2\pi}{T_{\text{rot}}} $$ Con $ T_{\text{rot}} \approx 24,\text{h} $.
- Momento angolare di rivoluzione
È associato al moto di rivoluzione attorno al Sole, che la Terra compie in circa 365 giorni. In questo caso, il momento angolare dipende dalla massa della Terra, la distanza dal Sole, la velocità orbitale. Questo momento angolare è legato alla stabilità dell’orbita terrestre. Quando un corpo orbita attorno a un altro il momento angolare orbitale è $$ L_{\text{orb}} = m v r $$ oppure in forma vettoriale: $$ \mathbf{L}_{\text{orb}} = \mathbf{r} \times \mathbf{p} $$ Dove $ m $ è la massa della Terra, $ v $ è la velocità orbitale, $ r $ è la distanza Terra-Sole.Nota. Poiché anche nell’orbita vale la relazione $ v = \omega_{\text{orb}} r $ il momento angolare orbitale può essere anche riscritto nella forma $$ L_{\text{orb}} = m, r^2, \omega_{\text{orb}} $$ Con $ \omega_{\text{orb}} = \frac{2\pi}{T_{\text{orb}}} $ e $ T_{\text{orb}} \approx 365,\text{giorni} $.
In entrambi i casi si applica il principio di conservazione del momento angolare. È grazie a questa conservazione che la Terra mantiene la sua orbita stabile, l'asse terrestre resta orientato sempre nella stessa direzione nello spazio.
E così via.
