Il prodotto scalare tra vettori
Cos'è il prodotto scalare
Il prodotto scalare di due vettori è un numero (scalare) ottenuto moltiplicando il modulo di uno dei due vettori per il modulo della proiezione su questo vettore dell'altro vettore. $$ \vec{v_1} \cdot \vec{v_2} = | \vec{v_1} | \cdot | \vec{v_2} | \cdot \cos \theta $$ Dove θ è l'ampiezza dell'angolo tra i due vettori.
Il prodotto scalare è anche detto prodotto interno.
E' indicato con la notazione <v1,v2>, (v1,v2) oppure v1• v2
Attenzione. Il prodotto scalare di due vettori <v1,v2> è una grandezza scalare ossia un numero. Non è una grandezza vettoriale e non va confuso con il prodotto di un vettore per uno scalare k. Sono due operazioni algebriche differenti.
A cosa serve?
Il prodotto scalare ha alcune proprietà geometriche molto utili.
- il prodotto scalare di due vettori è nullo quando i vettori sono vettori ortogonali, ossia perpendicolari tra loro, formando un angolo di 90°.
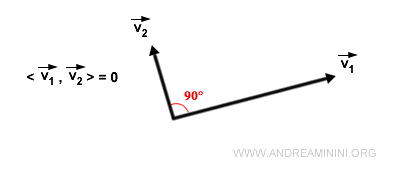
Questo accade perché il coseno di ±90° è zero. Quindi, il prodotto scalare nullo è una condizione necessaria di ortogonalità tra due o più vettori.- Nota. Non è una condizione sufficiente di ortogonalità perché il prodotto scalare è nullo <v1,v2>=0 anche se uno dei due vettori è un vettore nullo o entrambi sono vettori nulli.
- Il prodotto scalare di un vettore con se stesso è uguale a zero <v,v>=0 solo se il vettore v è un vettore nullo. $$ <\vec{v},\vec{v}> = 0 \ \Leftrightarrow \vec{v} = \{ ø \} $$
- Se il vettore v non è nullo allora il prodotto scalare con se stesso è uguale al quadrato del suo modulo. $$ <\vec{v},\vec{v}> = |\vec{v}|^2 \ \Leftrightarrow \ \vec{v} \ne \{ ø \} $$
Da questo emergono altre osservazioni utili.
- il prodotto scalare è uguale al prodotto dei moduli dei due vettori quando i vettori sono vettori paralleli o coincidenti, ossia hanno in comune la stessa direzione.
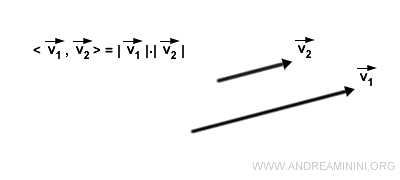
In questo caso il vettore proiettato sull'altro ha lo stesso modulo perché il coseno di un angolo nullo θ=0 è uguale a uno (cos 0° = 1). Quindi il prodotto scalare <v1,v2>coincide col prodotto dei moduli dei vettori |v1|·|v2| - Il prodotto scalare di un vettore per se stesso mi permette di calcolare la lunghezza (modulo o norma) del vettore
- Il prodotto scalare di due vettori mi permette di calcolare l'angolo tra i due vettori.
Le proprietà del prodotto scalare in sintesi. Le principali proprietà del prodotto scalare tra vettori da tenere sempre a mente.
A questa tabella aggiungo per completezza un caso banale. Anche il prodotto scalare con un vettore nullo è pari a zero, perché il vettore nullo ha modulo uguale a zero. Quindi il prodotto scalare pari a zero è una condizione necessaria ma non sufficiente di ortogonalità dei vettori.
Un esempio pratico
Ho due vettori nello spazio a due dimensioni R2
$$ \vec{ v_1} = \begin{pmatrix} 4 \\ 1 \end{pmatrix} $$
$$ \vec{ v_2 } = \begin{pmatrix} 2 \\ 2 \end{pmatrix} $$
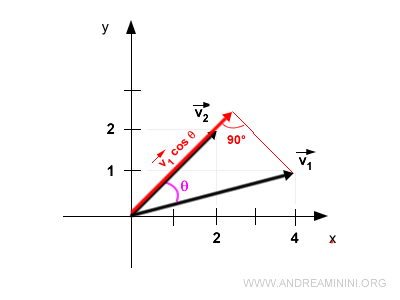
Ecco la rappresentazione grafica dei vettori
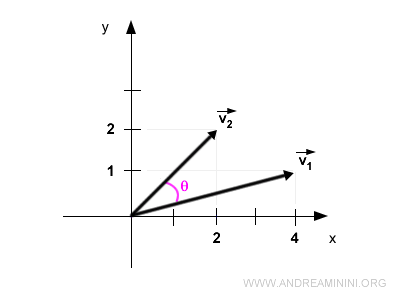
I due vettori formano un angolo di ampiezza θ = 30,96°.
Per calcolare il prodotto scalare
$$ < \vec{ v_1} , \vec{v_2} > = \vec{v_1} \cdot \vec{v_2} $$
Ora proietto il secondo vettore v2 sul primo v1 con un angolo di 90°.
In questo modo ottengo un nuovo vettore di modulo |v2|·cos θ nella stessa direzione del vettore v1.
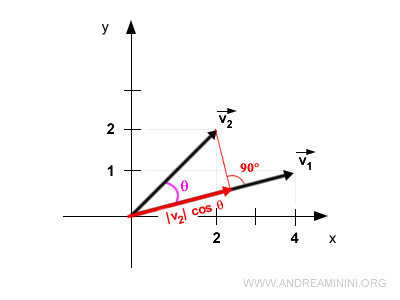
A questo punto moltiplico i due moduli tra loro e ottengo il prodotto scalare dei due vettori.
$$ < \vec{ v_1} , \vec{v_2} > = |\vec{v_1}| \cdot ( | \vec{v_2}| \cdot \cos \theta) $$
In questo caso i moduli (lunghezze) dei due vettori sono |v1|=4,12 e |v2|=2,83.
$$ < \vec{ v_1} , \vec{v_2} > = 4,12 \cdot ( 2,83 \cdot \cos \theta) $$
L'angolo tra i due vettori è θ = 30,96°
$$ < \vec{ v_1} , \vec{v_2} > = 4,12 \cdot ( 2,83 \cdot \cos 30,96°) $$
Sapendo che il coseno di 30,96° è 0,86
$$ < \vec{ v_1} , \vec{v_2} > = 4,12 \cdot ( 2,83 \cdot 0,86 ) $$
$$ < \vec{ v_1} , \vec{v_2} > = 4,12 \cdot ( 2,43 ) $$
Nota. Il prodotto 2,83·cos(30,96°) è il modulo del vettore rosso, quello che ho proiettato sul vettore v1 con modulo (lunghezza) pari a |v2|·cos θ.
$$ < \vec{ v_1} , \vec{v_2} > = 4,12 \cdot 2,43 $$
$$ < \vec{ v_1} , \vec{v_2} > = 10 $$
Quindi, il prodotto scalare dei due vettori v1 e v2 è uguale a 10.
Nota. Il prodotto scalare è commutativo. Quindi, se proiettando il primo vettore v1 sul secondo vettore v2, si ottiene lo stesso risultato <v2,v1>=<v1,v2>=10.
Metodo di calcolo alternativo più veloce
Per calcolare il prodotto scalare di due vettori posso anche usare il metodo del prodotto scalare euclideo.
$$ < \vec{ v_1} , \vec{v_2} > = v_{1x} \cdot v_{2x} + v_{1y} \cdot v_{2y} + v_{1z} \cdot v_{2z} $$
Ha il vantaggio d'essere molto più facile e rapido.
Basta moltiplicare le componenti dei vettori tra loro e sommarle.
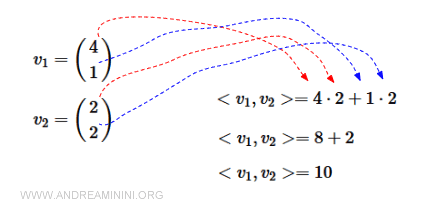
Dove 4·2 sono le componenti x dei vettori v1 e v2 mentre 1·2 sono le componenti y dei vettori v1 e v2
Il risultato è sempre lo stesso.
Le proprietà del prodotto scalare
Il prodotto scalare di due vettori appartenenti allo stesso spazio vettoriale V nel campo K=R è una funzione simmetrica e bilineare che associa alla coppia di vettori v1,v2 un elemento del campo K.
$$ <·,·> \:\: := \:\: VxV \:\: \rightarrow \:\: R $$
La funzione del prodotto scalare risponde alle seguenti proprietà:
Il prodotto scalare euclideo
Esistono diverse funzioni in grado di definire il prodotto scalare tra due vettori. La funzione più nota è il prodotto scalare euclideo. $$ <v_1 , v_2 > = v_{1x} \cdot v_{2x} + v_{1y} \cdot v_{2y} + v_{1z} \cdot v_{2z} $$
Un esempio pratico di prodotto scalare euclideo
Dati due vettori v1 e v2 appartenenti allo spazio vettoriale V=R3 nel campo K=R
$$ v_1 = \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} = \begin{pmatrix} 2 \\ -1 \\ 1 \end{pmatrix} $$
$$ v_2 = \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} = \begin{pmatrix} 3 \\ -1 \\ 0 \end{pmatrix} $$
Il prodotto scalare euclideo dei due vettori è il seguente:
$$ < v_1 , v_2 > = ( 2·3 ) + ( (-1)·(-1) ) + ( 1·0 ) $$
$$ < v_1 , v_2 > = 6+1+0 $$
$$ < v_1 , v_2 > = 7 $$
Nota. Il prodotto scalare è non degenere. Infatti, se <w,v>=0 per qualsiasi vettore w di V, allora il vettore v deve essere necessariamente nullo ossia v=0.
La dimostrazione
Parto dal prodotto scalare di due vettori<a,b>
$$ \vec{a} \cdot \vec{b} $$
Un vettore è uguale alla somma delle sue componenti x, y, z
$$ \vec{a} = a_x \vec{u_x} + a_y \vec{u_y} + a_z \vec{u_z} $$
$$ \vec{b} = b_x \vec{u_x} + b_y \vec{u_y} + b_z \vec{u_z} $$
Quindi, posso riscrivere il prodotto scalare in questa forma equivalente
$$ \vec{a} \cdot \vec{b} = ( a_x \vec{u_x} + a_y \vec{u_y} + a_z \vec{u_z} ) \cdot ( b_x \vec{u_x} + b_y \vec{u_y} + b_z \vec{u_z} ) = $$
Per la proprietà distributiva rispetto alla somma
$$ a_x \vec{u_x} b_x \vec{u_x} + a_x \vec{u_x} b_y \vec{u_y} + a_x \vec{u_x} b_z \vec{u_z} + $$
$$ a_y \vec{u_y} b_x \vec{u_x} + a_y \vec{u_y} b_y \vec{u_y} + a_y \vec{u_y} b_z \vec{u_z} + $$
$$ a_z \vec{u_z} b_x \vec{u_x} + a_z \vec{u_z} b_y \vec{u_y} + a_z \vec{u_z} b_z \vec{u_z} = $$
Sapendo che il prodotto scalare tra due vettori ortogonali è nullo
Nota.$$ \vec{u_x} \cdot \vec{u_y} = \vec{u_y} \cdot \vec{u_x} = 0 $$ $$ \vec{u_x} \cdot \vec{u_z} = \vec{u_z} \cdot \vec{u_x} = 0 $$ $$ \vec{u_y} \cdot \vec{u_z} = \vec{u_z} \cdot \vec{u_y} = 0 $$
Molti termini si annullano
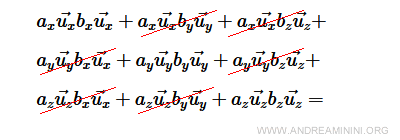
La somma si riduce a tre termini
$$ a_x \vec{u_x} b_x \vec{u_x} + a_y \vec{u_y} b_y \vec{u_y} + a_z \vec{u_z} b_z \vec{u_z} = $$
che posso scrivere in questa forma equivalente
$$ a_x b_x \vec{u_x} \vec{u_x} + a_y b_y \vec{u_y} \vec{u_y} + a_z b_z \vec{u_z} \vec{u_z} = $$
Il prodotto scalare di un vettore per se stesso è uguale al prodotto dei moduli, perché il coseno di un angolo nullo è uguale a 1.
Nota. $$ v \cdot v = |v||v| \cos 0 = |v|^2 $$
Sapendo che il modulo dei versori è uno, i prodotti scalari uxux=1, uyuy=1, uzuz=1.
$$ a_x b_x \cdot ( \vec{u_x} \vec{u_x} ) + a_y b_y \cdot ( \vec{u_y} \vec{u_y} ) + a_z b_z \cdot ( \vec{u_z} \vec{u_z} ) = $$
$$ a_x b_x \cdot (1 ) + a_y b_y \cdot ( 1 ) + a_z b_z \cdot ( 1 ) = $$
$$ a_x b_x + a_y b_y + a_z b_z $$
Questo dimostra che il prodotto scalare tra due vettori è uguale alla somma del prodotto delle sue componenti sugli assi x,y,z.
$$ \vec{a} \cdot \vec{b} =a_x b_x + a_y b_y + a_z b_z $$
La norma indotta dal prodotto scalare
Tra il prodotto scalare dei vettori e la norma (modulo) c'è una stretta relazione.
La norma di un vettore qualsiasi è uguale alla radice del prodotto scalare del vettore con se stesso.
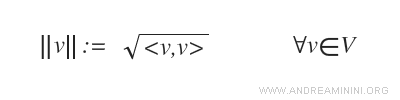
Questa norma è detta norma indotta dal prodotto scalare.
Nota. La norma indica la lunghezza del vettore ed è anche conosciuta come modulo del vettore.
Esempio
Dato un vettori v1 appartenente allo spazio vettoriale V=R3 nel campo K=R
$$ v_1 = \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} = \begin{pmatrix} 2 \\ -1 \\ 1 \end{pmatrix} $$
La norma indotta dei due vettori è la seguente:
$$ || v_1 || = < v_1 , v_1 > = \sqrt { <v_1 , v_1 > } $$
$$ || v_1 || = < v_1 , v_1 > = \sqrt { ( 2·2 ) + ( (-1)·(-1) ) + ( 1·1 ) } $$
$$ || v_1 || = < v_1 , v_1 > = \sqrt { 4+1+1 } $$
$$ || v_1 || = < v_1 , v_1 > = \sqrt { 6 } $$
Il teorema della diseguaglianza di Cauchy-Schwarz
Secondo il teorema di Cauchy-Schwarz
Il valore assoluto del prodotto scalare di due vettori <v1,v2> è minore o uguale al prodotto tra la norma indotta del prodotto scalare ||v1||·|| v2|| dei due vettori.
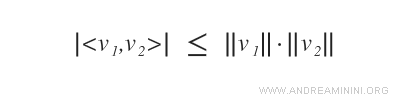
In caso di uguaglianza i due vettori v1, v2 sono linearmente dipendenti.
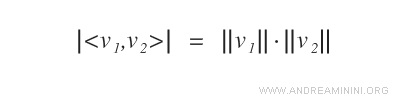
Un esempio pratico
Dati due vettori v1 e v2 appartenenti allo spazio vettoriale V=R3 nel campo K=R
$$ v_1 = \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} = \begin{pmatrix} 2 \\ -1 \\ 1 \end{pmatrix} $$
$$ v_2 = \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} = \begin{pmatrix} 3 \\ -1 \\ 0 \end{pmatrix} $$
Il valore assoluto del prodotto scalare <v1,v2> è il seguente:
$$ |< v_1 , v_2 >| = | 7 | = 7 $$
La norma indotta dei due vettori
$$ || v_1 || = \sqrt { (2*2)+(-1*-1)+(1*1) } = \sqrt {6} $$
$$ || v_2 || = \sqrt { (3*3)+(-1*-1)+(0*0) } = \sqrt {10} $$
Secondo il teorema di Cauchy-Schwarz
$$ |< v_1 , v_2 >| \le || v_1 || · || v_2 || $$
$$ 7 \le \sqrt {6} · \sqrt {10} $$
$$ 7 \le 7.7459 $$
Quindi, secondo il teorema, i due vettori non sono linearmente dipendenti tra loro.
Esempio 2
Ora provo a vedere cosa succede con due vettori linearmente dipendenti
$$ v_1 = \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} = \begin{pmatrix} -1 \\ 1 \end{pmatrix} $$
$$ v_2 = \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} = \begin{pmatrix} 1 \\ -1 \end{pmatrix} $$
Nota. Il determinante dei due vettori è uguale a zero. Quindi i due vettori sono linearmente dipendenti tra loro.
Il valore assoluto del prodotto scalare <v1,v2> è il seguente:
$$ |< v_1 , v_2 >| = | (-1·1)+(1·-1) | = 2 $$
La norma indotta dei due vettori
$$ || v_1 || = \sqrt { (-1*-1)+(1*1) } = \sqrt {2} $$
$$ || v_2 || = \sqrt { (1*1)+(-1*-1) } = \sqrt {2} $$
Secondo il teorema di Cauchy-Schwarz
$$ |< v_1 , v_2 >| \le || v_1 || · || v_2 || $$
$$ 2 \le \sqrt {2} · \sqrt {2} $$
$$ 2 = 2 $$
In questo caso sono uguali perché i due vettori sono linearmente dipendenti.
Il risultato conferma il teorema di Cauchy-Schwarz.
Osservazioni
Alcune osservazioni utili o interessanti sul prodotto scalare tra vettori
- A differenza del prodotto tra numeri reali, il prodotto scalare tra vettori può essere uguale a zero anche se entrambi i vettori non sono sono nulli. Ad esempio, se i vettori sono perpendicolari il coseno di 90° è uguale a zero. In questo caso i due vettori non sono nulli ma il loro prodotto scalare è uguale a zero.
- Se due vettori hanno la stessa direzione e verso, il prodotto scalare è uguale al prodotto dei moduli dei due vettori.
- Se due vettori hanno la stessa direzione ma verso opposto, il prodotto scalare è uguale all'opposto del prodotto dei moduli dei due vettori.
Come calcolare il prodotto scalare online
Questo strumento consente di calcolare il prodotto scalare di due vettori online.
