La distanza tra vettori
La distanza tra vettori è una misura che quantifica quanto due vettori siano "lontani" l’uno dall’altro nello spazio. Si calcola generalmente usando la norma della loro differenza dei vettori, cioè: \[ d(\vec{v}, \vec{w}) = |\vec{v} - \vec{w}| \]
Immagino due punti nello spazio tridimensionale, ma il ragionamento vale per qualsiasi dimensione.
Un punto si trova in \(\vec{v} = (x_1, y_1, z_1)\), l’altro in \(\vec{w} = (x_2, y_2, z_2)\).
La distanza tra questi due punti è proprio la lunghezza (norma) del vettore differenza \(\vec{v} - \vec{w}\):
\[ |\vec{v} - \vec{w}| = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2 + (z_1 - z_2)^2} \]
Questa formula è un'estensione del teorema di Pitagora nello spazio a tre dimensioni.
Nota. Quando si parla di distanza tra vettori, si assume sempre l'uso della norma euclidea (la radice quadrata della somma dei quadrati). Ma in alcuni casi si possono usare norme diverse, ad esempio, la distanza a scacchiera (o distanza di Manhattan) \(|x_1 - x_2| + |y_1 - y_2| \) e la distanza massima \(\max(|x_1 - x_2|, |y_1 - y_2|)\)
Esempio pratico
Considero due vettori in \(\mathbb{R}^2\):
\[ \vec{v} = \begin{pmatrix} 3 \\ 4 \end{pmatrix} \]
\[ \vec{w} = \begin{pmatrix} 5 \\ 1 \end{pmatrix} \]
Calcolo la loro distanza:
\[ \vec{v} - \vec{w} = \begin{pmatrix} 3 - 5 \\ 4 - 1 \end{pmatrix} = \begin{pmatrix} -2 \\ 3 \end{pmatrix} \]
Il modulo (lunghezza) del vettore differenza è
\[ |\vec{v} - \vec{w}| = \sqrt{(-2)^2 + 3^2} = \sqrt{4 + 9} = \sqrt{13} \]
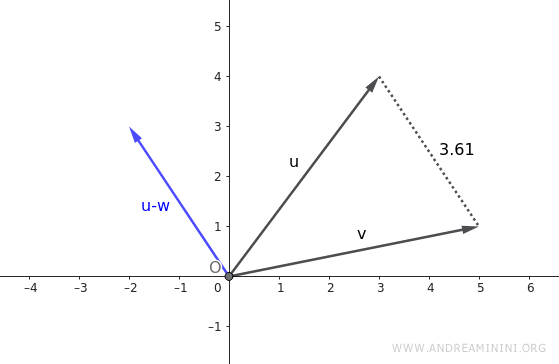
Quindi, la distanza tra i due vettori è \(\sqrt{13}\), cioè circa 3.6 unità.
Distanza tra i vettori in dimensioni superiori
La stessa formula vale anche in spazi con più dimensioni.
Ad esempio, considero due vettori nello spazio \(\mathbb{R}^4\) a quattro dimensioni.
\[ \vec{a} = \begin{pmatrix} 1 \\ 2 \\ 3 \\ 4 \end{pmatrix} \]
\[ \vec{b} = \begin{pmatrix} 3 \\ 0 \\ -1 \\ 2 \end{pmatrix} \]
Il vettore differenza tra i due vettori è:
\[ \vec{a} - \vec{b} = \begin{pmatrix} -2 \\ 2 \\ 4 \\ 2 \end{pmatrix} \]
\[ |\vec{a} - \vec{b}| = \sqrt{(-2)^2 + 2^2 + 4^2 + 2^2} = \sqrt{4 + 4 + 16 + 4} = \sqrt{28} \approx 5.29 \]
Nota. La distanza tra i vettori in uno spazio a più dimensione è molto usata in informatica per misurare la similarità tra dati (es. distanza tra due immagini, testi, etc.), nella grafica 3D e in algoritmi di machine learning come k-NN (k-nearest neighbors) o clustering.
E così via.
