Lo spazio vettoriale
Cos'è uno spazio vettoriale
Uno spazio vettoriale su un campo K è un insieme non vuoto di vettori V dotato di due operazioni binarie ( addizione tra vettori e moltiplicazione di un vettore per uno scalare ) che soddisfano determinate proprietà.
E' anche detto spazio lineare oppure K-spazio vettoriale.
Graficamente uno spazio vettoriale è l'insieme di tutti i vettori che hanno origine da un punto con le operazioni di addizione tra vettori e moltiplicazione dei vettori per uno scalare.
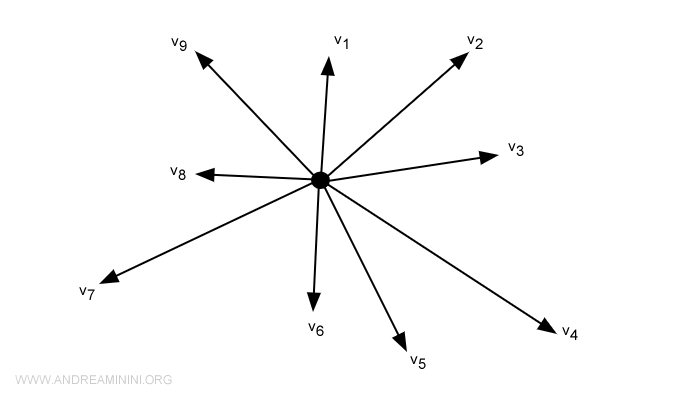
Nota. A livello intuitivo gli elementi di uno spazio vettoriali sono dei vettori. Tuttavia, in generale uno spazio vettoriale può essere composto anche da altri oggetti. Ad esempio, uno spazio vettoriale di matrici o uno spazio vettoriale di polinomi.
Quali sono i componenti di uno spazio vettoriale?
I componenti di uno spazio vettoriale sono i seguenti:
- Un campo (K) i cui elementi sono detti scalari.
- Un insieme non vuoto (V) i cui elementi sono detti vettori.
- Due operazioni binarie, la somma tra vettori e la moltiplicazione di un vettore per scalare, che soddisfano tutte le seguenti proprietà
- Proprietà commutativa $$ \vec{v}+\vec{w}=\vec{w}+\vec{v} \ \ \ \ \ \ \vec{v}, \vec{w} \in V $$
- Proprietà associativa $$ ( \vec{u}+\vec{v} ) +\vec{w} = \vec{u} + ( \vec{v}+\vec{w} ) \ \ \ \ \ \ \vec{v}, \vec{w}, \vec{u} \in V $$
- Esistenza vettore nullo $$ \exists \ \vec{0} \ \in V \ \ | \ \ \vec{v}+\vec{0} = \vec{0}+\vec{v} = \vec{v} $$
- Esistenza vettore opposto $$ \forall \ \vec{v} \ \ \exists \ -\vec{v} \ \in V \ \ | \ \ \vec{v}+(-\vec{v}) = \vec{0}+\vec{v} = \vec{v} $$
- Prodotto di uno scalare per un vettore $$ (a \cdot b) \cdot \vec{v} = a \cdot (b \cdot \vec{v} ) \ \ \ \ a,b \in K \ \ \ \vec{v} \in V $$
Nota. Il punto di moltiplicazione indica due operazioni di natura diversa. Il prodotto a*b è un prodotto tra due scalari nel campo K mentre (a*b)*v è un prodotto di uno scalare (a*b) per un vettore v.
- Proprietà distributiva $$ (a + b) \cdot \vec{v} = a \cdot \vec{v} + b \cdot \vec{v} \ \ \ \ \ \ \ \ a,b \in K \ \ \ \vec{v} \in V $$ $$ a \cdot (\vec{v} + \vec{w}) = a \cdot \vec{v} + a \cdot \vec{w} \ \ \ \ \ \ \ \ a \in K \ \ \ \vec{v}, \vec{w} \in V $$
- Elemento neutro della moltiplicazione $$ 1 \cdot \vec{v} = \vec{v} \ \ \ \ \ \ \ \ \forall \vec{v} \in V $$
Va sottolineato che le proprietà delle operazioni nello spazio vettoriale V sono simili ma si distinguono dalle proprietà delle operazioni nel campo K.
Nello spazio vettoriale V sono operazioni tra vettori o tra vettori e scalari, nel campo K invece sono operazioni tra scalari.
Pertanto, in uno spazio vettoriale le operazioni tra gli scalari devono soddisfare le proprietà del campo K, le operazioni con i vettori devono soddisfare le proprietà dello spazio vettoriale V.
Per un approfondimento sulle proprietà delle operazioni in uno spazio vettoriale.
Cos'è un campo? In matematica un campo è una struttura algebrica composta da un insieme non vuoto K e da due operazioni binarie ( somma e prodotto ) indicate con + e *.
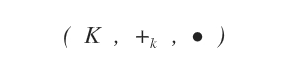
Se il campo K è l'insieme dei numeri reali R, lo spazio è detto spazio vettoriale reale. Se il campo è l'insieme dei numeri complessi C, lo spazio è detto spazio vettoriale complesso.
Un esempio di spazio vettoriale
Esempio 1: lo spazio vettoriale R1
Lo spazio vettoriale R1 è uno spazio vettoriale a una dimensione (n=1) nel campo dei numeri reali K=R, in cui sono definite le operazioni di somma tra vettori e moltiplicazione di un vettore per uno scalare.
Essendo n=1 lo spazio vettoriale coincide con il campo dei numeri reali
$$ R^1 = \{ (a_1) \} \ \ \ \ \ \ a_1 \in R $$
Ogni punto della retta coincide un numero reale.
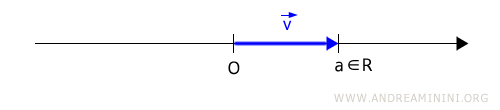
Fissata un'origine (O) ogni punto della retta è un vettore di lunghezza (modulo) pari a un numero reale.
Nota. Nello spazio vettoriale R1 i vettori hanno tutti la stessa direzione, sono orientati in un verso o nell'altro e hanno una lunghezza(modulo) diverso.
Ecco alcuni esempi di vettori in R1
$$ \vec{v_1} = 3 \ \ \ \ \vec{v_2} = 5 \ \ \ \ \vec{v_3} = -1 \ \ \ ... $$
Le operazioni di somma di vettori e moltiplicazione di uno scalare per un vettore in R1 soddisfano le proprietà degli spazi vettoriali.
Esempio 2: lo spazio vettoriale R2
Se n=2 lo spazio vettoriale R2 (ossia RxR) coincide con il piano cartesiano dei numeri reali.
$$ R^2 = \{ (a_1,a_2) \} \ \ \ \ \ \ a_1,a_2 \in R $$
Dove RxR è il prodotto cartesiano dell'insieme dei numeri reali.
In questo caso a ogni coppia di numeri reali (x,y) corrisponde un punto del piano della geometria euclidea, ossia un vettore a due dimensioni.
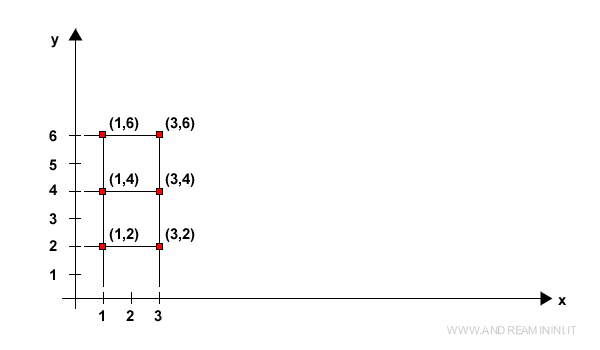
Quindi, lo spazio vettoriale reale è composto da R2 vettori.
Ecco alcuni esempi di vettori composti da n=2 elementi nel campo dei numeri reali R.
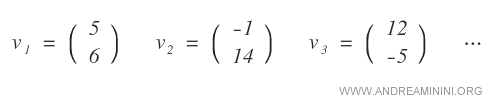
Nota. Essendo l'insieme dei numeri reali R un insieme infinito, anche lo spazio vettoriale reale R2 è infinito.
Nello spazio vettoriale R2 sono definite le due operazioni binarie: somma tra vettori e prodotto di un vettore per uno scalare.
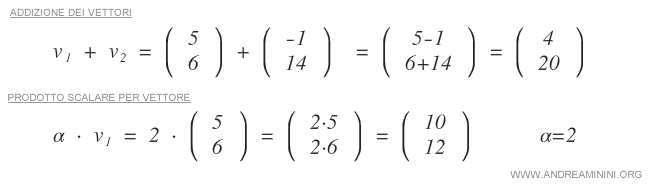
Le operazioni rispettano tutte le proprietà delle operazioni negli spazi vettoriali.

Ho così dimostrato che R2 è uno spazio vettoriale sul campo R.
Posso applicare lo stesso metodo per qualsiasi altro spazio vettoriale reale con Rn vettori numerici.
Esempio 3: lo spazio vettoriale R3
Se n=3 lo spazio vettoriale R3 (ossia RxRxR) coincide con lo spazio a tre dimensioni.
$$ R^3 = \{ (a_1,a_2, a_3) \} \ \ \ \ \ \ a_1,a_2, a_3 \in R $$
In questo caso a ogni tripla di numeri reali (x,y,z) corrisponde un punto nello spazio, ossia un vettore a tre dimensioni dove a1=x, a2=y, a3=z.
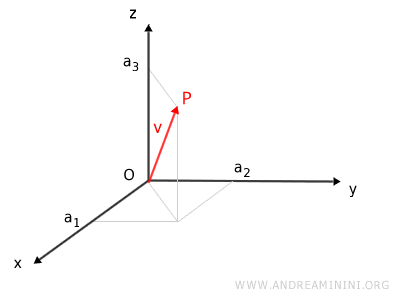
Anche nello spazio vettoriale R3 sono definite le due operazioni binarie: somma tra vettori e prodotto di un vettore per uno scalare.
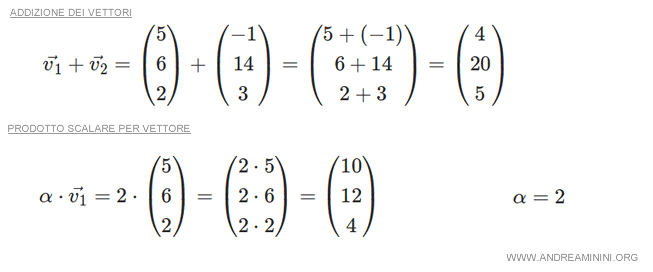
Le operazioni rispettano tutte le proprietà degli spazi vettoriali.
Esempio 4: lo spazio vettoriale R4
Se n=4 lo spazio vettoriale R4 (ossia RxRxRxR) è uno spazio a quattro dimensioni.
E' uno spazio composto da vettori con quattro componenti (a1, a2, a3, a4)
$$ R^4 = \{ (a_1,a_2, a_3, a_4) \} \ \ \ \ \ \ a_1,a_2, a_3, a_4 \in R $$
Anche nello spazio vettoriale R4 sono definite le due operazioni binarie (somma tra vettori e prodotto di un vettore per uno scalare) e le operazioni rispettano tutte le proprietà degli spazi vettoriali.
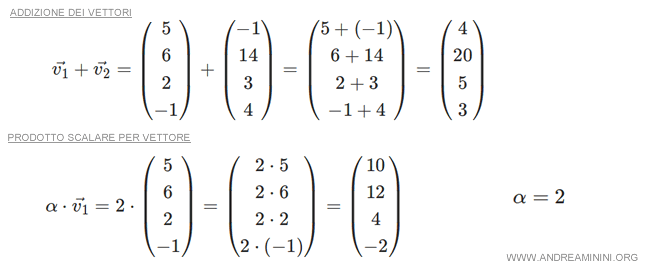
Nota. E' difficile immaginare uno spazio vettoriale a 4 o più dimensioni, perché siamo abituati a vivere in uno spazio geometrico a tre dimensioni. E' più facile per noi immaginare spazi a dimensioni inferiori (1 o 2 dimensioni) piuttosto che uno spazio a 4 dimensioni. Ciò nonostante gli spazi vettoriali esistono anche per dimensioni superiori a 3.
Esempio 5: lo spazio vettoriale Rn
Lo spazio vettoriale Rn è il prodotto cartesiano RxRx...xR dove R è moltiplicato per se stesso n volte.
$$ R^n = \{ (a_1, a_2, a_3, ... , a_n) \} \ \ \ \ \ \ a_i \in R $$
Ogni elemento dello spazio vettoriale Rn è un vettore con n componenti, ossia una n-pla ordinata di numeri reali a1, ... , an.
$$ \vec{v} = \begin{pmatrix} a_1 \\ a_2 \\ a_3 \\ \vdots \\ a_n \end{pmatrix} \ \ \ \ \ \ \ \vec{v} \in V = R^n $$
Quindi, lo spazio vettoriale Rn è lo spazio delle n-plue ordinate di elementi del campo K=R.
Nello spazio vettoriale Rn sono definite le due operazioni binarie:
- L'addizione di due vettori v1 e v2 è un altro vettore appartenente allo stesso spazio vettoriale.
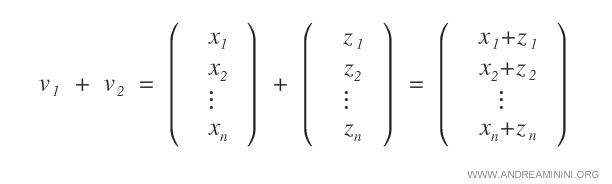
- Il prodotto di uno scalare α per un vettore v è un vettore appartenente allo stesso spazio vettoriale.
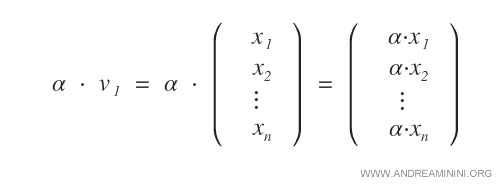
Le due operazioni rispettano tutte le proprietà di uno spazio vettoriale.
Nota. Le proprietà ( assiomi ) di uno spazio vettoriale sono le seguenti: associativa, commutativa, distributiva del prodotto rispetto all'addizione dei vettori, distributiva del prodotto rispetto all'addizione degli scalari, esistenza di un elemento neutro, esistenza di un elemento opposto, compatibilità del prodotto, compatibilità dell'elemento neutro.
Norma e prodotto scalare
Lo spazio vettoriale non comprende i concetti di lunghezza e angolo del vettore.
Per introdurli nello spazio vettoriale occorre usare una struttura aggiuntiva che include due oggetti matematici:
- Norma. E' il concetto matematico che definisce la lunghezza (o modulo) di un vettore.
- Prodotto scalare. E' il concetto matematico che definisce l'angolo tra due vettori.
Nota. Esistono diverse strutture tra cui poter scegliere. Ogni struttura ha differenti definizioni di norma e prodotto scalare. Pertanto, non c'è una sola definizione possibile di angolo e di lunghezza del vettore.
La combinazione lineare
Una delle operazioni più frequenti in uno spazio vettoriale è la combinazione lineare.
La combinazione lineare è un'operazione tra vettori e scalari in uno spazio vettoriale V definito nel campo K=R. $$ \vec{w} = a_1 \cdot \vec{v_1} + a_2 \cdot \vec{v_2} + a_3 \cdot \vec{v_3} + ... + a_n \cdot \vec{v_n} $$ E' un vettore (w) ottenuto tramite la somma del prodotto tra n coefficienti scalari (a) e n vettori (v).
Dove w, v1, v2, ... ,vn sono vettori dello spazio vettoriale V
$$ \vec{w}, \vec{v_1}, \vec{v_2}, ... , \vec{v_n} \in V $$
Mentre i coefficienti a1, a2, ... , an sono numeri (scalari) ossia elementi del campo dei numeri reali K=R.
$$ a_1, a_2, ... , a_n \in K=R $$
Vettori linearmente dipendenti e indipendenti
La combinazione lineare mi permette di capire quali vettori dello spazio vettoriale sono
- Vettori linearmente indipendenti
I vettori v1, v2,..., vn sono linearmente indipendenti se l'unica soluzione alla combinazione lineare per ottenere un vettore nullo $$ a_1 \cdot \vec{v_1} + a_2 \cdot \vec{v_2} + ... + a_n \cdot \vec{v_n} = \vec{0} $$ è la combinazione banale con tutti i coefficienti scalari nulli ai = 0 $$ a_1 = a_2 = ... = a_n = 0 $$ - Vettori linearmente dipendenti
I vettori v1, v2,..., vn sono linearmente dipendenti se esiste una o più soluzioni non banali alla combinazione lineare per ottenere un vettore nullo, in cui almeno un coefficiente scalare ai ≠ 0 è diverso da zero. $$ a_1 \cdot \vec{v_1} + a_2 \cdot \vec{v_2} + ... + a_n \cdot \vec{v_n} = \vec{0} $$ In questo caso i coefficienti ai per ottenere un vettore nullo non sono tutti nulli. $$ \exists \ a_i \ne 0 $$
In pratica, due o più vettori sono linearmente dipendenti tra loro quando non sono linearmente indipendenti.
Tipi di spazi vettoriali
Gli spazi vettoriali sono suddivisi in due categorie
- Spazi vettoriali finitamente generati
Sono spazi vettoriali generati da un numero finito di vettori. - Spazi vettoriali non finitamente generati
Sono spazi vettoriali generati da un numero infinito di vettori.
E così via.
