Corrispondenza biunivoca tra vettori e punti del piano

Ogni punto $ P $ del piano alle coordinate $ (x, y) $ può essere associato a un vettore $ \vec{v} = \begin{pmatrix} x \\ y \end{pmatrix} $, detto vettore posizione, che ha come punto di partenza l'origine $ O $ e come punto di arrivo $ P $. E viceversa.
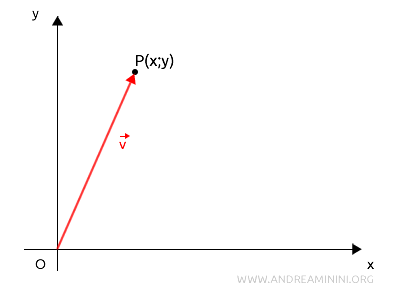
esempio

In altre, parole, esiste una perfetta corrispondenza tra i punti del piano $ P $ e i vettori nello spazio vettoriale $ \mathbb{R}^2 $.

Quindi, posso immaginare che i punti del piano e i vettori di $ \mathbb{R}^2 $ siano "due modi di vedere la stessa cosa": un punto può essere rappresentato da un vettore e un vettore identifica un punto preciso.

Questa associazione dipende dalla scelta di un'origine $ O $, che funge da riferimento per definire i vettori posizione.

L'associazione tra punti del piano e vettori in $ \mathbb{R}^2 $ è biunivoca perché:

Ogni punto del piano ha un unico vettore posizione
Ogni punto $ P(x, y) $ è rappresentato da un solo vettore $ \vec{OP} = \begin{pmatrix} x \\ y \end{pmatrix} $.
Ogni vettore rappresenta un solo punto
Un vettore $ \begin{pmatrix} x \\ y \end{pmatrix} $ corrisponde a un unico punto $ P(x, y) $ nel piano.

Esempio

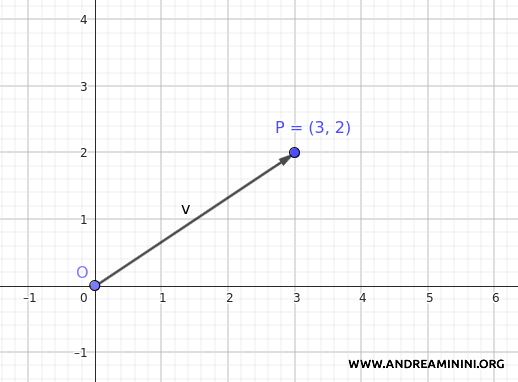
Ad esempio, se un punto del piano ha coordinate $ P(3, 2) $, il vettore che lo rappresenta è:

$$ \vec{OP} = \begin{pmatrix} 3 \\ 2 \end{pmatrix} $$

Viceversa, dato un vettore $ \vec{v} = \begin{pmatrix} 3 \\ 2 \end{pmatrix} $, posso associarlo al punto $ P(3, 2) $ nel piano.

un esempio pratico

E così via.