Angolo tra due vettori
Per calcolare l'angolo tra due vettori utilizzo l'arcocoseno del rapporto tra il prodotto scalare dei vettori e il prodotto dei moduli dei vettori. $$ \alpha = \arccos ( \frac{\vec{v} \cdot \vec{w}}{ |\vec{v}| \cdot |\vec{w}|} )$$
Anche se i vettori si trovano in quadranti diversi, la formula resta sempre la stessa.
Questa formula restituisce sempre l’angolo compreso tra 0° e 180° cioè l’angolo "più piccolo" tra i due vettori, indipendentemente dalla loro posizione nel piano.
Un esempio pratico
Ho due vettori
$$ \vec{v} = \begin{pmatrix} 1 \\ 3 \end{pmatrix} $$
$$ \vec{w} = \begin{pmatrix} 4 \\ 2 \end{pmatrix} $$
Dal punto di vista grafico
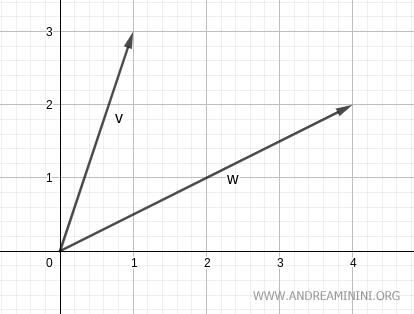
Calcolo l'angolo tra i due vettori usando la formula
$$ \alpha = \arccos ( \frac{\vec{v} \cdot \vec{w}}{ |\vec{v}| \cdot |\vec{w}|} )$$
Il prodotto scalare dei vettori è
$$ \vec{v} \cdot \vec{w} = \begin{pmatrix} 1 \\ 3 \end{pmatrix} \cdot \begin{pmatrix} 4 \\ 2 \end{pmatrix} = 1 \cdot 4 + 3 \cdot 2 = 4+6= 10$$
Quindi sostituisco 10 al numeratore
$$ \alpha = \arccos ( \frac{\vec{v} \cdot \vec{w}}{ |\vec{v}| \cdot |\vec{w}|} )$$
$$ \alpha = \arccos ( \frac{10}{ |\vec{v}| \cdot |\vec{w}|} )$$
Calcolo i moduli dei due vettori usando il teorema di Pitagora
$$ |\vec{v}| = \sqrt{3^2+1^2} = \sqrt{10} $$
$$ |\vec{w}| = \sqrt{4^2+2^2} = \sqrt{20} $$
Poi sostituisco i moduli al denominatore
$$ \alpha = \arccos ( \frac{10}{ |\vec{v}| \cdot |\vec{w}|} )$$
$$ \alpha = \arccos ( \frac{10}{ \sqrt{10} \cdot \sqrt{20}} )$$
$$ \alpha = \arccos ( \frac{10}{ \sqrt{200} } )$$
$$ \alpha = \arccos ( 0,71 )$$
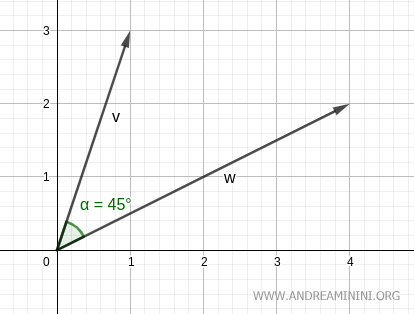
L'arcocoseno di 0,71 è 45°
$$ \alpha = 45° $$
Pertanto, l'angolo tra i due vettori è 45°
Esempio 2
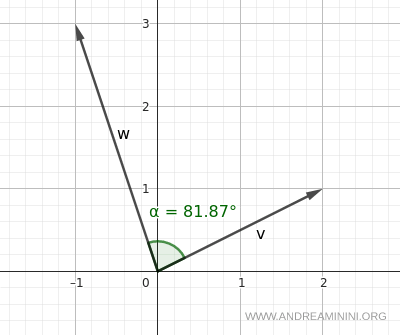
Considero due vettori in quadranti diversi
$$\vec{v} = \begin{pmatrix} 2 \\ 1 \end{pmatrix} \quad \text{(primo quadrante)}$$
$$ \vec{w} = \begin{pmatrix} -1 \\ 3 \end{pmatrix} \quad \text{(secondo quadrante)} $$
Il prodotto scalare tra i due vettori è
$$ \vec{v} \cdot \vec{w} = 2 \cdot (-1) + 1 \cdot 3 = -2 + 3 = 1 $$
I moduli dei due vettori sono:
$$ |\vec{v}| = \sqrt{2^2 + 1^2} = \sqrt{5} $$
$$ |\vec{w}| = \sqrt{(-1)^2 + 3^2} = \sqrt{10} $$
Quindi, l'angolo tra i due vettori è
$$ \alpha = \arccos\left( \frac{1}{\sqrt{5} \cdot \sqrt{10}} \right) = \arccos\left( \frac{1}{\sqrt{50}} \right) \approx \arccos(0.141) \approx 81.87^\circ $ $$
L'angolo tra i due vettori è 81,87°.
$$ \alpha \approx 81.87^\circ $$
Pertanto, se i vettori si trovano in quadranti diversi influisce sul segno delle componenti, la formula mi restituisce comunque l'angolo tra i due compreso tra 0° e 180°. Non essendo un angolo orientato, quindi non può essere 270°.
La dimostrazione
Il prodotto scalare di due vettori è uguale al prodotto dei moduli per il coseno dell'angolo compreso tra i due vettori.
$$ \vec{v} \cdot \vec{w} = |\vec{v}| \cdot |\vec{w}| \cdot \cos \alpha $$
Metto in evidenza il coseno dell'angolo alfa
$$ \cos \alpha = \frac{ \vec{v} \cdot \vec{w} }{|\vec{v}| \cdot |\vec{w}| } $$
Poi calcolo l'arcocoseno a entrambi i membri dell'equazione
$$ \arccos( \cos \alpha ) = \arccos( \frac{ \vec{v} \cdot \vec{w} }{|\vec{v}| \cdot |\vec{w}| } ) $$
L'arcocoseno è la funzione inversa del coseno.
Quindi, l'arcocoseno del coseno di alfa è l'angolo alfa
$$ \alpha = \arccos( \frac{ \vec{v} \cdot \vec{w} }{|\vec{v}| \cdot |\vec{w}| } ) $$
Ho dimostrato la formula che permette di calcolare l'ampiezza dell'angolo compreso tra due vettori.
E così via.
