Momento torcente
Il momento torcente (o momento di una forza) misura la capacità di una forza di far ruotare un corpo attorno a un punto o a un asse. La formula base è: $$ M = F \cdot d $$ Dove $F$ è l'intensità della forza, $d$ è il braccio della forza (raggio), ossia la distanza perpendicolare tra la retta d’azione della forza e il punto (o asse) di rotazione.
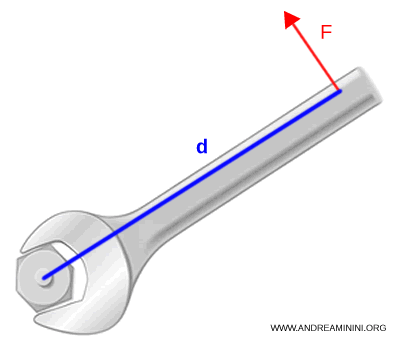
Se la forza non è perpendicolare, si calcola:$$M = F \cdot d \cdot \sin \theta$$ dove $\theta$ è l’angolo tra la direzione della forza e il braccio.
Per calcolare il momento torcente non basta applicare una forza, è necessario anche conoscere dove e in che direzione viene applicata rispetto al punto di rotazione.
Per convenzione, al momento torcente si attribuisce
- segno positivo $(M > 0)$ se la rotazione è in verso antiorario
- segno negativo $(M < 0)$ se la rotazione è in verso orario
La convenzione può comunque variare in base al contesto.
Nota. Quando agiscono più momenti torcenti, il segno di ciascuno si determina considerando l’effetto che produrrebbe se fosse applicato da solo. La risultante complessiva si ottiene quindi come somma algebrica dei singoli momenti.
Esempio
Per svitare un bullone utilizzo una chiave inglese lunga 0,3 m con cui applico una forza di 20 N perpendicolarmente al braccio.

Il momento torcente sul bullone sarà 6 N·m (newton per metro)
$$ M = 20 \times 0,3 = 6 \, \text{N·m} $$
Ora utilizzo una chiave inglese più lunga, ad esempio 0,6 m, e applico la stessa forza (20 N) perpendicolarmente.
$$ M = 20 \times 0,6 = 12 \, \text{N·m} $$
Il momento torcente della forza si è raddoppiato.
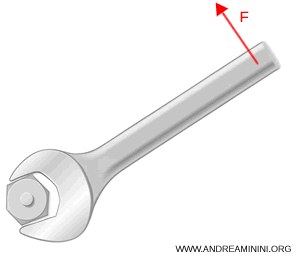
Questo vuol dire che più distante è il punto di applicazione dal punto o asse di rotazione, più facilmente si svita il bullone.
In parole semplici: una chiave più lunga mi permette di fare meno fatica, perché aumenta il momento torcente senza dover aumentare la forza.
Nota. Per la stessa ragione la maniglia di una porta è situata lontano dai cardini, ossia lontano dall'asse di rotazione della porta. Spingere una porta vicino ai cardini richiede più forza ed è molto più faticoso che spingerla dalla maniglia.

Ad esempio, se impiego una forza di 10 N per aprire la porta, se la spingo da 1 metro dai cardini il momento è 10 N·m $$ M = F \times d = 10 \ N \times 1 \ m = 10 \, \text{N·m} $$ Spingendo a soli 0,2 metri dai cardini, per ottenere lo stesso momento ( $ M=10 \ N \cdot m $) servirebbe una forza cinque volte maggiore: $$ F = \frac{M}{d} = \frac{10 \ N \cdot m}{0,2 \ m} = 50 \, \text{N} $$
La formula del momento torcente
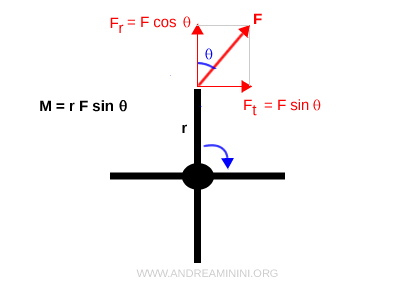
Una forza $\vec{F}$, applicata in un punto a distanza $ r $ dal centro di rotazione di un corpo rigido, può generare una rotazione. L’effetto di questa forza è misurato dal momento torcente (o momento della forza) $M$, definito dalla relazione $$ M = r F \sin \theta $$ Dove $\theta$ è l’angolo compreso tra il vettore posizione e la direzione della forza.
Quando applico la forza radialmente, cioè lungo il raggio che congiunge il punto di applicazione all’asse di rotazione, il momento torcente è nullo $ M = 0 $
In questo caso non si produce alcuna rotazione.
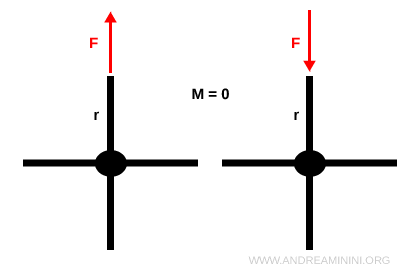
Al contrario, se applico una forza perpendicolarmente al raggio, si genera il momento torcente massimo, perché tutta la sua intensità contribuisce alla rotazione.
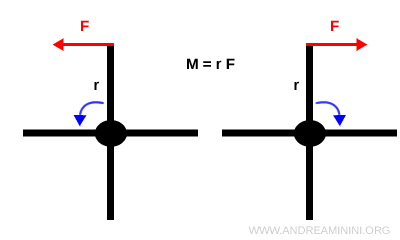
In generale, infatti, solo la componente tangenziale della forza è responsabile della rotazione, mentre la componente radiale non ha alcun effetto.
Per questo motivo, il momento torcente si calcola proiettando la forza sulla direzione tangenziale:
$$ M = r \, (F \sin \theta) $$
La componente radiale della forza può, invece, essere ignorata.
Esercizi
Esercizio 1
Calcola il momento torcente prodotto da una forza di intensità $ F=40 \ N $ applicata a una distanza $ r = 0,20 \ m $ dall'asse di rotazione con un angolo di 30° rispetto al braccio della leva.
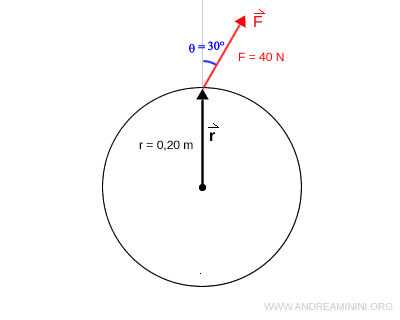
Per calcolare il momento torcente si utilizza la formula
$$ M = r \cdot F \cdot \sin \theta $$
Dove $ r \ m $ è la distanza dell'asse di rotazione, ossia la lunghezza del braccio della leva $ \vec{r} $ che in questo caso è $ r=0,20 \ m $.
$$ M = 0,20 \ m \cdot F \cdot \sin \theta $$
L'intensità della forza è $ F=40 \ N $
$$ M = 0,20 \ m \cdot 40 \ N \cdot \sin \theta $$
L'angolo tra il vettore $ \vec{F} $ della forza applicata e il braccio della leva $ \vec{r} $ è \$theta = 30° $.
$$ M = 0,20 \ m \cdot 40 \ N \cdot \sin 30° $$
Sapendo che il seno di 30° è $ \sin 30° = \frac{1}{2} $
$$ M = 0,20 \ m \cdot 40 \ N \cdot \frac{1}{2} $$
In questo modo trovo la forza tangenziale ossia $ F_x = 40 \ N \cdot \frac{1}{2} = 20 \ N $
$$ M = 0,20 \ m \cdot 20 \ N $$
Pertanto, il momento della forza è 4 N per metro.
$$ M = 4 \ Nm $$
E così via.
