Momento di un vettore
Cos'è il momento di un vettore
Il momento di un vettore v applicato al punto P rispetto a un punto O detto polo è il prodotto vettoriale tra il vettore posizione OP e il vettore stesso v. $$ \vec{M} = \vec{OP} × \vec{v} $$ Il modulo del momento è $$ | \vec{M} | = | \vec{OP} | \cdot | \vec{v} | \cdot \sin θ $$
Dove θ è l'angolo formato dai due vettori v e OP.
Il momento del vettore è a sua volta una grandezza vettoriale.
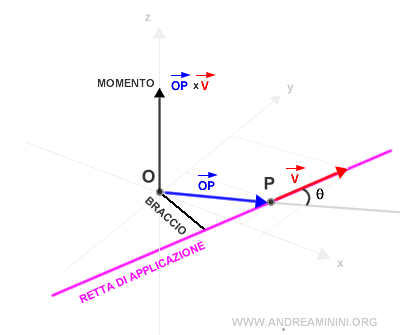
E' un vettore perpendicolare al piano che contiene il vettore v e il vettore posizione OP, perché è il risultato di un prodotto vettoriale.
Nota. La direzione del vettore v è detta retta di applicazione del vettore v. La distanza minima tra la retta di applicazione e il polo O è detta braccio del vettore v rispetto al polo O.
Le proprietà del momento di un vettore
Le principali proprietà del momento di un vettore.
- Il modulo del momento del vettore è nullo quando il vettore v e il vettore posizione OP hanno la stessa direzione. Quindi, il modulo del momento è zero se i vettori sono paralleli o coincidenti. Non è nullo se hanno direzioni diverse.
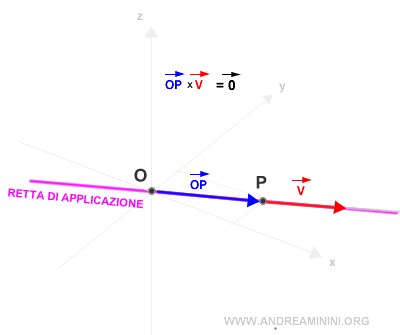
Nota. In questo caso la lunghezza del braccio è zero perché la retta di applicazione passa per il polo O. Il momento è un vettore nullo.
- Spostando il vettore v lungo la sua retta di applicazione, il modulo del momento del vettore non cambia. Questo vuol dire che il momento ha una proprietà di conservazione.
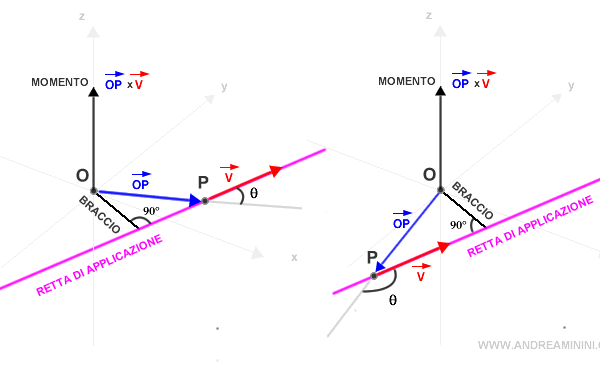
La spiegazione
Prendo in considerazione un vettore applicato in un punto P e un punto O come polo.
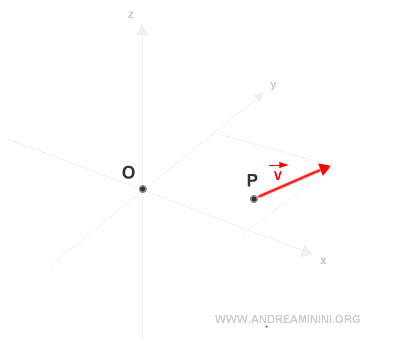
Calcolo il vettore posizione di v rispetto al punto O.
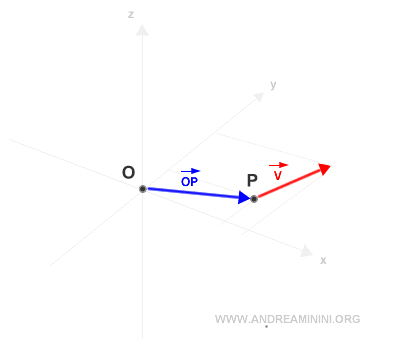
Traccio le rette dei due vettori per indicare le rispettive direzioni.
La direzione del vettore è detta retta di applicazione.
Poi calcolo l'ampiezza dell'angolo θ tra i due vettori.
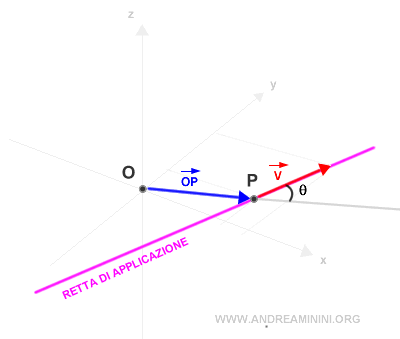
La distanza della retta di applicazione dal polo è detta braccio.
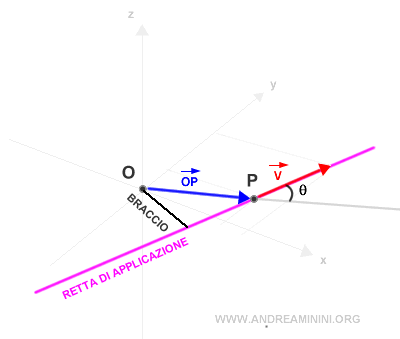
A questo punto calcolo il prodotto vettoriale tra il vettore posizione OP e il vettore v.
Il risultato è un vettore perpendicolare detto momento del vettore v rispetto al polo O.
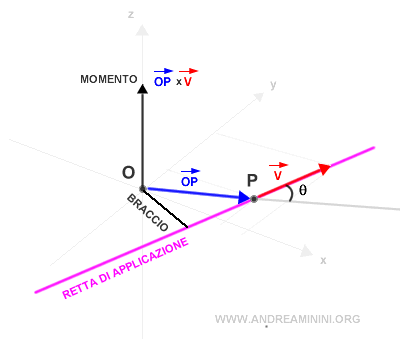
Il cambiamento del polo
Il polo rappresenta il sistema di riferimento (o base).

Un eventuale cambiamento del polo da O a O' sul piano cartesiano modifica il momento del vettore.
Il nuovo vettore del momento MO' ha la stessa direzione del precedente ma diversa lunghezza (modulo).
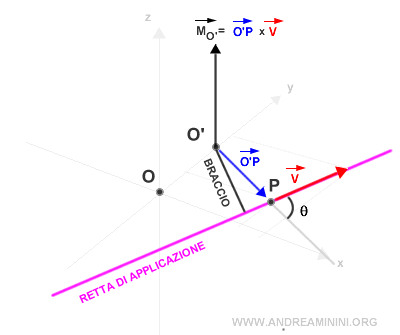
Il cambiamento del polo modifica l'angolo θ, il braccio e la lunghezza del momento del vettore.
I due momenti MO e MO' del vettore v sono comunque legati tra loro dalla relazione algebrica
$$ \vec{M_{O'}} = \vec{O'O} × \vec{v} + \vec{M_O} $$
Dimostrazione
Il momento del vettore v rispetto al polo O è
$$ \vec{M_O} = \vec{OP} × \vec{v} $$
Il momento del vettore v rispetto al polo O' è
$$ \vec{M_{O'}} = \vec{O'P} × \vec{v} $$
Il vettore posizione O'P è uguale alla somma dei vettori O'O+OP.
Quindi posso anche scrivere
$$ \vec{M_{O'}} = ( \vec{O'O} + \vec{OP} ) × \vec{v} $$
Applico la proprietà distributiva del prodotto vettoriale rispetto alla somma
$$ \vec{M_{O'}} = \vec{O'O} × \vec{v} + \vec{OP} × \vec{v} $$
Sapendo che MO=OP × v
$$ \vec{M_{O'}} = \vec{O'O} × \vec{v} + \vec{M_O} $$
Ho dimostrato la relazione tra i due momenti del vettore rispetto a due diversi poli O e O'.
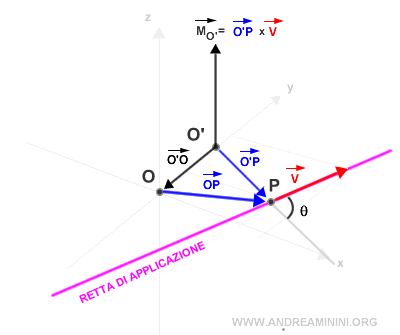
Quindi, il modulo del nuovo momento |MO'| dopo il cambio di base è
$$ | \vec{M_{O'}} | = | \vec{O'O} × \vec{v} | + | \vec{M_O} | $$
Nota. Se dopo il cambiamento del polo il vettore O'O è parallelo al vettore v, il momento del vettore è sempre lo stesso perché il braccio non cambia. $$ \vec{O'O} \ || \ \vec{v} \ \ \Rightarrow \ \ M_{O'}=M_O $$ Ecco la rappresentazione grafica di questo caso particolare.
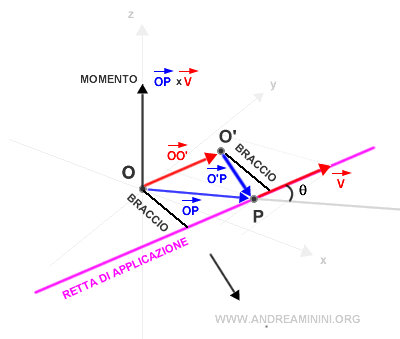
E così via.
