Il gradiente

Il gradiente di una funzione o campo scalare f(x,y,z) è un campo vettoriale le cui componenti sono le derivate parziali di f rispetto agli assi cartesiani di riferimento (x,y,z). $$ ∇ f = \frac{ d \ f}{d \ x} \vec{u}_x + \frac{ d \ f}{d \ y} \vec{u}_y + \frac{ d \ f}{d \ z} \vec{u}_z $$ E' un operatore differenziale e si indica con l'operatore differenziale nabla ∇, un triangolo verso il basso oppure con la dicitura grad $$ grad f = \frac{ d \ f}{ d \ x} \vec{u}_x + \frac{ d \ f}{ d \ y} \vec{u}_y + \frac{ d \ f}{ d \ z} \vec{u}_z$$.

Dove u_x, u_y, u_z sono i versori degli assi x, y, z dello spazio vettoriale a tre dimensioni.

Il campo scalare f(x,y,y) è una funzione a valori reali.

Il gradiente ∇f è, invece, una funzione vettoriale.

A cosa serve il gradiente?

Il gradiente trasforma una funzione scalare (o campo scalare) in un vettore. Misura la variazione di una grandezza scalare in una direzione.

Ad esempio, il gradiente termico misura la variazione della temperatura in una particolare direzione dello spazio.

Nota. Il gradiente è utile per trovare la direzione in cui il campo scalare f(x,y,z) cresce più rapidamente. Il modulo del gradiente è uguale al tasso di variazione del campo scalare.

Le proprietà del gradiente

Dato un gradiente ∇f e un vettore v, il prodotto scalare ∇f·v è uguale al valore della derivata direzionale di f rispetto a v

$$ ∇f \cdot \vec{v} = D_v \ f $$

Cos'è la derivata direzionale? La derivata direzionale è la derivata di una funzione f(x,y,z) rispetto a una particolare direzione indicata dal vettore v. $$ D_v \ f = \lim_{h \rightarrow 0} \frac{f(x+h \cdot \vec{v}, \ y+h \cdot \vec{v}, \ z+h \cdot \vec{v})-f(x,y,z)}{h} $$ E' un'estensione del concetto di derivata parziale che invece si calcola rispetto agli assi di riferimento (x,y,z). $$ D_x \ f = \lim_{ \Delta x \rightarrow 0} \frac{f(x+\Delta x, y, z)-f(x,y,z)}{ \Delta x} $$

Se considero un incremento infinitesimo nella direzione del vettore posizione v (raggio vettore)

$$ d \ \vec{v} = dx \cdot \vec{u_x} + dy \cdot \vec{u_y} + dz \cdot \vec{u_z} $$

La derivata direzionale della funzione rispetto a questa direzione è uguale al gradiente ∇f

$$ \frac{d \ f(\vec{v})}{d \ \vec{v}} = ∇f $$

Quindi, il differenziale della funzione df rispetto a questa direzione è

$$ df(\vec{v}) = ∇f \cdot d \vec{v} $$

E di conseguenza

$$ f(\vec{v} + d \vec{v})= f(\vec{v}) + df(\vec{v}) = f(\vec{v})+ ∇f(\vec{v}) \cdot \vec{v} $$

Un esempio pratico

Considero la funzione di due variabili

\[ f(x, y) = x^2 + y^2 \]

Questa funzione associa a ogni punto \( (x, y) \) il quadrato della distanza dall'origine.

Per calcolare il gradiente \( \nabla f \), derivo parzialmente rispetto a \( x \) e \( y \):

\[ \frac{\partial f}{\partial x} = 2x \]

\[ \frac{\partial f}{\partial y} = 2y \]

Quindi, il gradiente della funzione è:

\[ \nabla f(x, y) = 2x \, \vec{u}_x + 2y \, \vec{u}_y \]

oppure, in forma vettoriale:

\[ \nabla f(x, y) = \begin{pmatrix} 2x \\ 2y \end{pmatrix} \]

Il gradiente punta radialmente verso l'esterno dall'origine, in effetti segue la direzione in cui \( f(x, y) = x^2 + y^2 \) cresce più rapidamente.

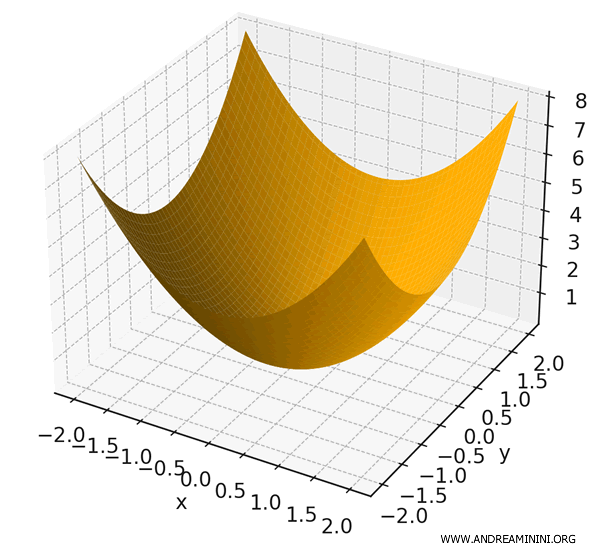
Il modulo del gradiente è \( |\nabla f| = \sqrt{(2x)^2 + (2y)^2} = 2\sqrt{x^2 + y^2} \), che rappresenta il tasso di variazione della funzione al crescere della distanza dall'origine.

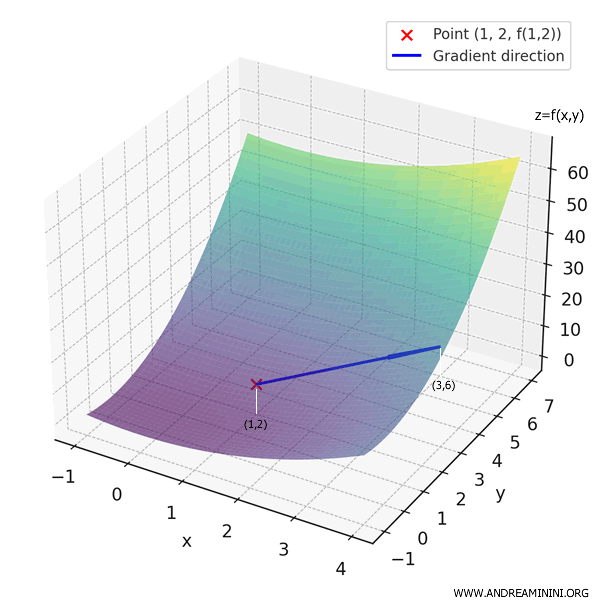
Ad esempio, se scelgo il punto \( (1, 2) \), allora:

\[ \nabla f(1, 2) = \begin{pmatrix} 2 \cdot 1 \\ 2 \cdot 2 \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \end{pmatrix} \]

Quindi al punto \( (1, 2) \), la funzione cresce più rapidamente nella direzione del vettore \( (2, 4) \), cioè verso il punto \( (1,2)+(2,4)= (3, 6) \).

Lo stesso calcolo posso ripeterlo per qualsiasi punto del piano (x,y).

Il risultato finale è il campo vettoriale del gradiente della funzione \( f(x, y) = x^2 + y^2 \) nel piano:

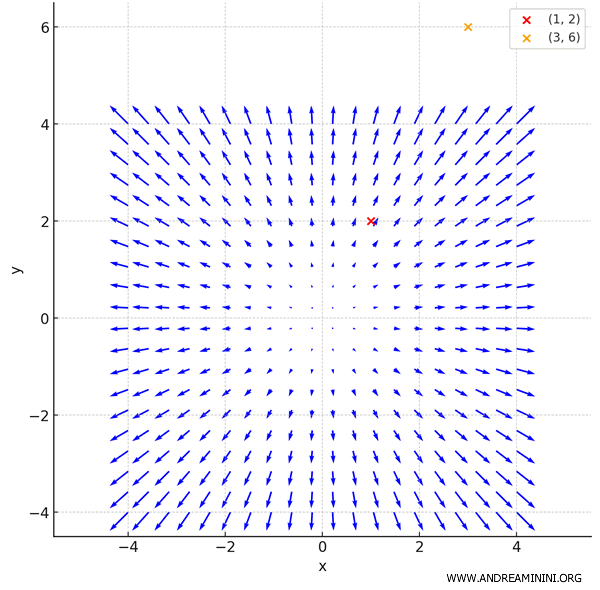
Ogni freccia rappresenta il vettore gradiente in un punto \( (x, y) \)

I vettori puntano verso l’esterno, cioè lontano dall’origine, perché la funzione cresce man mano che ci si allontana dal centro

I punti \( (1,2) \) e \( (3,6) \) sono evidenziati in rosso e arancione

Volendo posso aggiungere anche delle curve di livello (contour lines) che rappresentano i punti dove la funzione ha approssimativamente lo stesso valore \( f(x, y) = c \).

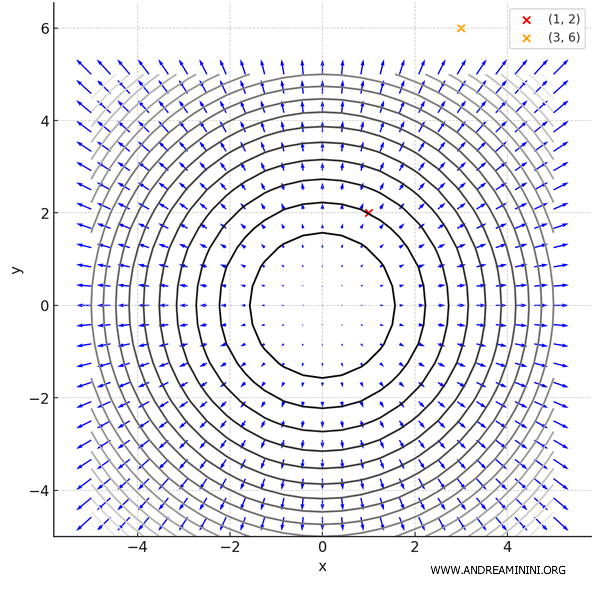
In questo caso le curve di livello sono cerchi concentrici, perché \( f(x, y) = x^2 + y^2 \).

Il gradiente punta nella direzione di massima crescita d una funzione

Il gradiente \( \nabla f(x_0) \) è un vettore che punta nella direzione di massima crescita della funzione.

In altre parole, il gradiente rappresenta la drezione di massima pendenza della funzione, quella in cui si sale più rapidamente.

La lunghezza del gradiente indica quanto velocemente la funzione cresce in quella direzione.

Viceversa, il vettore opposto al gradiente indica la direzione in cui la funzione decresce più rapidamente.

Esempio

Considero la funzione

$$ f(x,y) = x^2 + y^2 $$

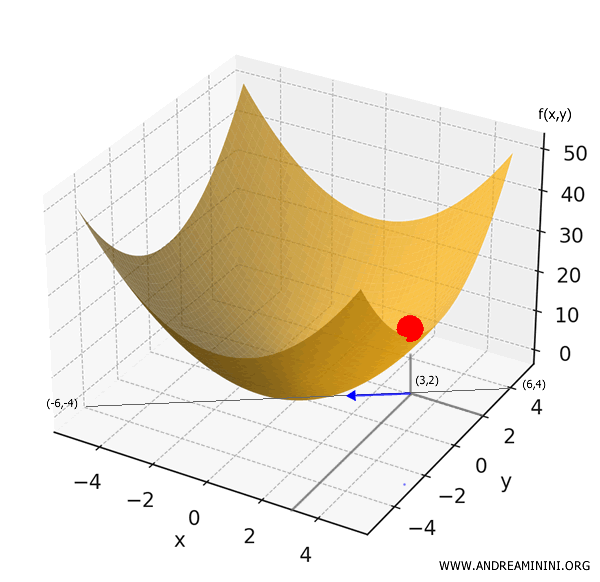
Questa funzione ha la forma di una ciotola. L'ho già vista nell'esempio precedente.

Se lascio cadere una pallina nel punto (3,2), in quale direzione si muoverà la pallina?

Per prima cosa calcolo le derivate parziali della funzione per x e y.

$$ f_x = 2x $$

$$ f_y = 2y $$

Questo mi permette di ottenere il gradiente della funzione

$$ \nabla f(x,y) = ( 2x,2y ) $$

Applico il gradiente al punto (3,2) ossia x=3 e y=2.

$$ \nabla f(3,2) = ( 2 \cdot 3 , 2 \cdot 2)=(6,4) $$

Il gradiente punta sempre verso la direzione di massima crescita della funzione (cioè "in salita").

Una pallina soggetta alla gravità, però, rotola "in discesa": segue cioè la direzione di massima diminuzione del valore di \( f \). Questa direzione è l’opposto del gradiente:

$$ -\nabla f(3,2) = (-6,-4) $$

Quindi, la pallina si muoverà in direzione (-6,-4).

Nota. Volendo posso anche calcolare la direzione normalizzata. \[ \mathbf u=\frac{-\nabla f(3,2)}{\lVert\nabla f(3,2)\rVert} =\frac{(-6,-4)}{\sqrt{6^2+4^2}} =\Bigl(-\tfrac{3}{\sqrt{13}},\,-\tfrac{2}{\sqrt{13}}\Bigr) \] dividendo il vettore direzione per la sua norma (modulo). L'interpretazione fisica e geometrica è sempre la stessa.

Dimostrazione

Considero la definizione della derivata direzionale di una funzione \( f \) nel punto \( x_0 \), lungo una direzione data dal vettore \( \vec{v} \).

Questa è data dal prodotto scalare tra il gradiente di \( f \) nel punto \( x_0 \) e il vettore \( \vec{v} \):

\[ \frac{\partial f}{\partial \vec{v}}(\vec{x}_0) = \nabla f(x_0) \cdot \vec{v} \]

Poiché si tratta di un prodotto scalare tra due vettori, posso esprimerlo come il prodotto dei moduli per il coseno dell'angolo compreso tra i due vettori:

\[ \frac{\partial f}{\partial \vec{v}}(x_0) = |\nabla f(x_0)| \cdot |\vec{v}| \cdot \cos\theta \]

Dove \( \theta \) è l’angolo compreso tra il gradiente \( \nabla f(x_0) \) e la direzione \( \vec{v} \).

Questa espressione mi dice che il valore della derivata direzionale dipende da tre fattori:

1. dalla norma del gradiente, che misura l’intensità della variazione della funzione;
2. dalla lunghezza del vettore direzione \( \vec{v} \), che di norma si prende con modulo 1;
3. dal coseno dell’angolo tra il gradiente e la direzione considerata.

La norma del gradiente \( |\nabla f(x_0)| \) non dipende dalla direzione che scelgo mentre la norma del vettore direzione è generalmente presa con modulo unitario \( | \vec{v} | = 1 \), quindi il risultato dipende soprattutto dal valore del coseno.

Vediamo ora come varia il coseno al variare dell’angolo:

• Se \( \theta = 0^\circ \), allora \( \cos\theta = 1 \): i due vettori sono paralleli e puntano nella stessa direzione. In questo caso, la derivata direzionale assume il suo valore massimo e la direzione corrisponde a quella del gradiente.
• Se \( \theta = 180^\circ \), allora \( \cos\theta = -1 \): i vettori sono paralleli ma di verso opposto. Qui la derivata direzionale è minima, e la direzione è opposta al gradiente.
• Se \( \theta = 90^\circ \), cioè i vettori sono ortogonali, si ha \( \cos\theta = 0 \). In questo caso, la derivata direzionale è nullo: la funzione non varia in quella direzione.

Da tutto ciò possiamo concludere che il gradiente \( \nabla f(x_0) \) indica la direzione di massima crescita della funzione e la sua norma rappresenta il tasso massimo di variazione in quella direzione.

La relazione tra gradiente e linee di livello

Il gradiente è sempre perpendicolare alle linee di livello.

Questo significa che se disegno una linea di livello, come un cerchio, il gradiente in ogni punto della linea è un vettore ortogonale a quella curva ed esce radialmente dal cerchio.

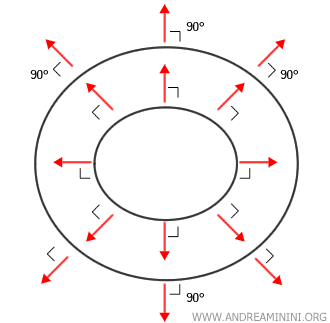
Le linee di livello sono le curve lungo le quali la funzione ha lo stesso valore $ f(x,y)=c $.

Il gradiente, invece, rappresenta la direzione di massima crescita della funzione $ \nabla f(x, y) = \left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right) $

Quindi, se in una certa direzione la funzione non cambia (linea di livello), e in un’altra cambia al massimo (gradiente), queste due direzioni devono essere perpendicolari tra loro ossia devono formare un angolo di 90°.

Esempio

Il gradiente della funzione $ f(x,y)=x^2+y^2 $ genera un campo vettoriale perché associa a ogni punto del piano un vettore che punta verso la direzione di massima crescita e all'opposto a quella di massima decrescita.

Come si può vedere ogni vettore gradiente che ha origine in un punto $ (x,y,z) $ della superficie della funzione $ f(x,y) $,  dove $ z = f(x,y) $, è perpendicolare alla linea di livello che passa in quel punto.

Solo al centro delle linee di livello della funzione $ f(x,y)=x^2+y^2 $ c'è un vettore nullo $ (x,y,z)=(0,0,0) $ che non punta in nessuna direzione.

Nota. Il gradiente nullo indica un punto critico, cioè dove la funzione non cresce né cala in nessuna direzione. In questi casi conviene calcolare il laplaciano, ossia la somma delle derivate seconde rispetto a tutte le variabili spaziali. \[\Delta f = \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2}\] Il laplaciano, in quel punto, mi dice se stai su un minimo (\( \Delta f > 0 \)), un massimo (\( \Delta f < 0 \)), oppure se la situazione è ambigua (\( \Delta f = 0 \)) e devo studiare più a fondo il caso.

Dimostrazione

Considero un punto \( (x_0, y_0) \) e una curva \( \gamma(t) = (x(t), y(t)) \) che rimane sulla linea di livello di \( f \).

Quindi, la derivata direzionale lungo la linea di livello è nulla

\[ f(x(t), y(t)) = \text{costante} \quad \Rightarrow \quad \frac{d}{dt} f(x(t), y(t)) = 0 \]

Uso la regola della catena:

\[ \frac{d}{dt} f(x(t), y(t)) = \frac{\partial f}{\partial x} \cdot \frac{dx}{dt} + \frac{\partial f}{\partial y} \cdot \frac{dy}{dt} = \nabla f \cdot \vec{v} = 0 \]

Dove \( \vec{v} = \left( \frac{dx}{dt}, \frac{dy}{dt} \right) \) è il vettore tangente alla curva \( \gamma(t) \).

Se il prodotto scalare tra il gradiente \( \nabla f \) e il vettore tangente \( \vec{v} \) è zero, allora i due vettori sono ortogonali.

Quindi, il gradiente è ortogonale (perpendicolare) alle linee di livello.

E così via.