Prodotto vettoriale

Cos'è il prodotto vettoriale nello spazio

Il prodotto vettoriale è una moltiplicazione tra vettori che genera un nuovo vettore. L'operazione si legge "u vettore v". $$ \vec{u} \ × \ \vec{v} = \vec{w} $$ In alternativa si può scrivere anche $$ \vec{u} \ ∧ \ \vec{v} = \vec{w} $$ Il modulo del prodotto vettoriale è $$ |\vec{w}| = |\vec{u}| \cdot |\vec{v}| \cdot \sin \alpha_{uv} $$

E' un'operazione tra due vettori nello spazio euclideo R³ che determina un terzo vettore.

Il risultato del prodotto vettoriale è una grandezza vettoriale.

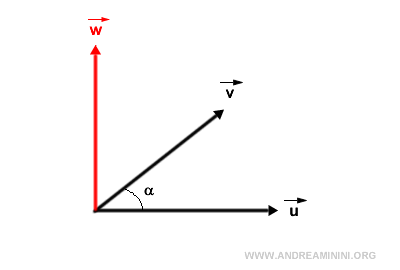
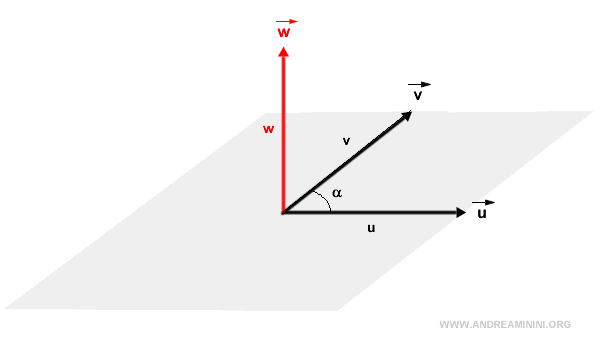
Il prodotto vettoriale (w) è un vettore normale rispetto agli altri due. Quindi, è perpendicolare agli altri due vettori.

Generalmente l'operazione del prodotto vettoriale si indica con il simbolo x oppure con il simbolo ∧.

Le proprietà del prodotto vettoriale in sintesi. Le principali proprietà del prodotto vettoriale da tenere sempre a mente.

Le caratteristiche geometriche del prodotto vettoriale

Il vettore w ottenuto con il prodotto vettoriale ha le seguenti caratteristiche

• Il modulo del prodotto vettoriale (vettore w) è pari all'area del parallelogramma formato dai vettori u e v
  
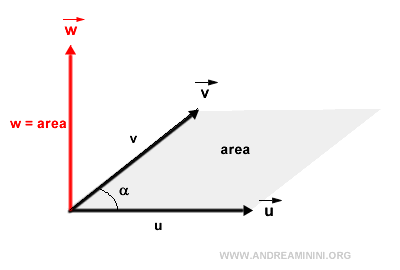
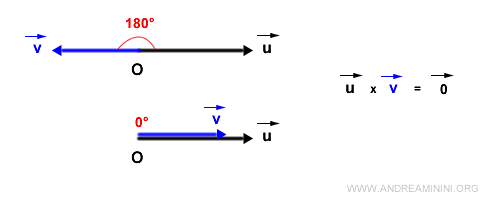
  Dal punto di vista trigonometrico il modulo del vettore w è pari pari al prodotto dei moduli dei vettori u e v, presi in valore assoluto, per il seno dell'angolo orientato α_uv compreso tra i vettori u e v. $$ |\vec{w}| = |\vec{u}| \cdot |\vec{v}| \cdot \sin \alpha_{uv} $$ In altri termini è il prodotto tra il primo vettore u e la proiezione del secondo vettore v.

  Nota. Da questo emergono alcune proprietà utili del prodotto vettoriale. Quando i due vettori hanno la stessa direzione il prodotto vettoriale è nullo perché l'area formata dai vettori è nulla. Pertanto, se i vettori formano un angolo di 180° (vettori opposti) o 0° (vettori coincidenti) il loro prodotto vettoriale è un vettore nullo ossia un vettore con modulo pari a zero.
  
  Se invece i due vettori sono ortogonali (vettori normali) ossia formano un angolo di 90° il modulo del prodotto vettoriale è pari al prodotto dei loro moduli perché il seno dell'angolo è +1.
  
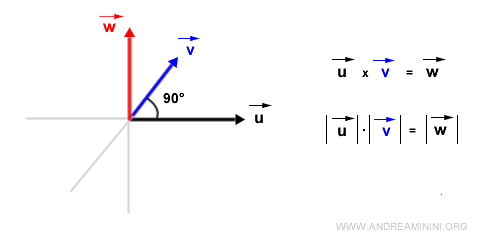
  Se formano un angolo orientato di -90° il modulo del prodotto vettoriale è pari al prodotto dei moduli dei vettori ma con segno opposto, perché ora il seno dell'angolo è -1. Quindi, il prodotto vettoriale ha verso opposo rispetto al caso precedente.
  

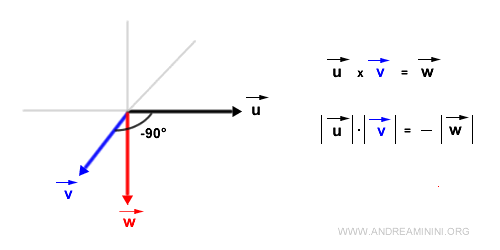
• La direzione del prodotto vettoriale (vettore w) è perpendicolare al piano del parallelogramma formato dai vettori u e v.
  
• Il verso del prodotto vettoriale (vettore w) si ottiene con il metodo della mano destra. Il pollice è il primo vettore u, l'indice è il secondo vettore, il medio indica il verso del vettore w.
  
  

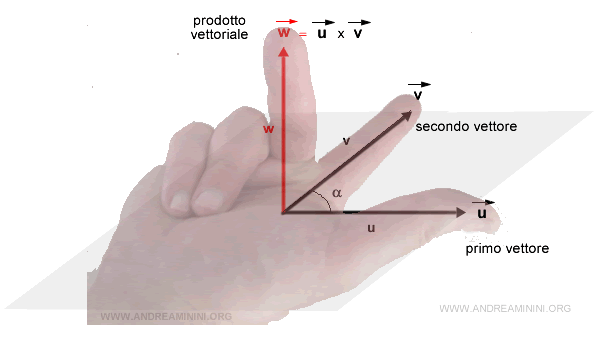
  Attenzione. Il pollice deve essere sovrapposto sempre sul primo vettore del prodotto vettoriale e l'indice sul secondo.

  Metodo alternativo per capire il verso
  Individuo il piano che contiene entrambi i vettori e guardo i vettori dall'alto. Se la rotazione più rapida per sovrapporre il primo vettore (u) sul secondo vettore (v) è antiorario, il prodotto vettoriale w = u x v esce dal piano verso l'alto (verso di me). Si parla anche di metodo della vite destrorsa con verso da destra verso sinistra.
  
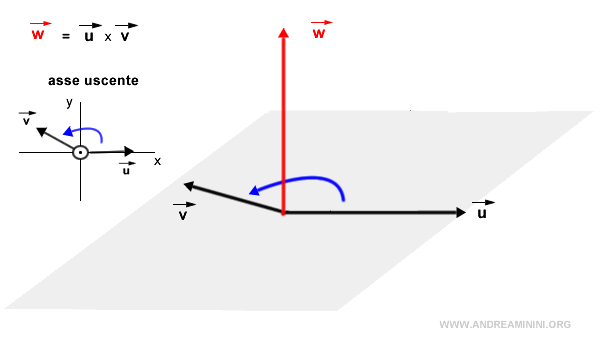
  Se invece la rotazione più rapida per sovrapporre il primo vettore (u) sul secondo vettore (v) è in senso orario, il prodotto vettoriale w = u x v entra nel piano verso il basso, ossia dalla parte opposta al piano rispetto a me.
  
  

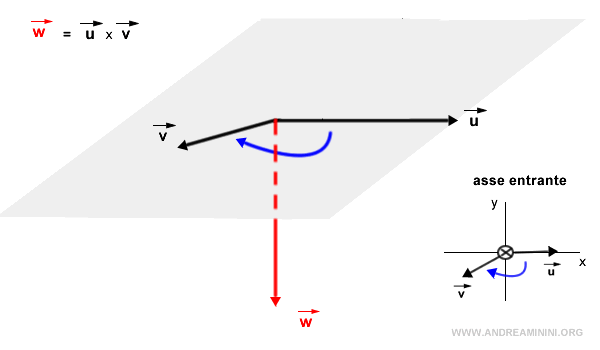
  Nota. In generale, guardando il piano dall'alto della punta del vettore del prodotto vettoriale w = u x v la rotazione più rapida per sovrapporre il primo vettore (u) sul secondo vettore (v) è sempre antioraria.

Come calcolare il prodotto vettoriale

Per il calcolo del prodotto vettoriale posso usare due metodi.

Metodo 1

$$ \vec{v_1} ∧ \vec{v_2} = \begin{pmatrix} x_1 \\ y_1 \\ z_1 \end{pmatrix} \cdot \begin{pmatrix} x_2 \\ y_2 \\ z_2 \end{pmatrix} = \begin{pmatrix} det \begin{pmatrix} y_1 & y_2 \\ z_1 & z_2 \end{pmatrix} \\ - det \begin{pmatrix} x_1 & x_2 \\ z_1 & z_2 \end{pmatrix} \\ det \begin{pmatrix} x_1 & x_2 \\ y_1 & y_2 \end{pmatrix} \end{pmatrix} $$

Metodo 2

$$ \vec{v_1} ∧ \vec{v_2} = \begin{pmatrix} x_1 \\ y_1 \\ z_1 \end{pmatrix} \cdot \begin{pmatrix} x_2 \\ y_2 \\ z_2 \end{pmatrix} = det \begin{pmatrix} i & x_1 & x_2 \\ j & y_1 & y_2 \\ k & z_1 & z_2 \end{pmatrix} $$

Un esempio pratico

Nello spazio tridimensionale R³ ho due vettori.

$$ \vec{v_1} = \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} $$

$$ \vec{v_2} = \begin{pmatrix} 1 \\ -3 \\ 2 \end{pmatrix} $$

Calcolo il prodotto vettoriale v₁ ∧ v₂ con il primo e il secondo metodo

Metodo 1

$$ \vec{v_1} ∧ \vec{v_2} = \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} \cdot \begin{pmatrix} 1 \\ -3 \\ 2 \end{pmatrix} = \begin{pmatrix} det \begin{pmatrix} 2 & -3 \\ 1 & 2 \end{pmatrix} \\ - det \begin{pmatrix} 1 & 1 \\ 1 & 2 \end{pmatrix} \\ det \begin{pmatrix} 1 & 1 \\ 2 & -3 \end{pmatrix} \end{pmatrix} $$

Sviluppo i tre determinanti

$$ \vec{v_1} ∧ \vec{v_2} = \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} \cdot \begin{pmatrix} 1 \\ -3 \\ 2 \end{pmatrix} = \begin{pmatrix} 2 \cdot 2 - (-3) \cdot 1 \\ - ( 1 \cdot 2 - 1 \cdot 1 ) \\ 1 \cdot (-3) - 1 \cdot 2 \end{pmatrix} = \begin{pmatrix} 7 \\ -1 \\ -5 \end{pmatrix}$$

Ho così trovato un terzo vettore ortogonale con i precedenti vettori, ossia con un angolo di 90°.

Verifica. Se due vettori sono ortogonali il loro prodotto scalare è nullo. $$ < \begin{pmatrix} 7 \\ -1 \\ -5 \end{pmatrix} , \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} > = 7 \cdot 1 + (-1) \cdot 2 + (-5) \cdot 1 = 7 -2 -5 = 0 $$ $$ < \begin{pmatrix} 7 \\ -1 \\ -5 \end{pmatrix} , \begin{pmatrix} 1 \\ -3 \\ 2 \end{pmatrix} > = 7 \cdot 1 + (-1) \cdot (-3) + (-5) \cdot 2 = 7 +3 -10 = 0 $$ Pertanto, il vettore appena calcolato è ortogonale con i precedenti.

Metodo 2

$$ \vec{v_1} ∧ \vec{v_2} = \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} \cdot \begin{pmatrix} 1 \\ -3 \\ 2 \end{pmatrix} = det \begin{pmatrix} i & 1 & 1 \\ j & 2 & -3 \\ k & 1 & 2 \end{pmatrix} $$

$$ \vec{v_1} ∧ \vec{v_2} = i \begin{pmatrix} 2 & -3 \\ 1 & 2 \end{pmatrix} - j \begin{pmatrix} 1 & 1 \\ 1 & 2 \end{pmatrix} + k \begin{pmatrix} 1 & 1 \\ 2 & -3 \end{pmatrix} $$

$$ \vec{v_1} ∧ \vec{v_2} = 7i -j -5k $$

I coefficienti dei versori i, j, k sono il prodotto vettoriale dei due vettori.

$$ \vec{v_1} ∧ \vec{v_2} = \begin{pmatrix} 7 \\ -1 \\ -5 \end{pmatrix}$$

Il risultato coincide con il metodo 1.

Le proprietà del prodotto vettoriale

Il prodotto vettoriale rispetta le seguenti proprietà

Proprietà anticommutativa
Il prodotto vettoriale non è commutativo. E' anticommutativo. $$ \vec{a} ∧ \vec{b} = -\vec{b} ∧ \vec{a} $$ Proprietà distributiva rispetto alla somma
Il prodotto vettoriale soddisfa la proprietà distributiva rispetto alla somma. $$ \vec{a} ∧ (\vec{b} + \vec{c} ) = (\vec{a} ∧ \vec{b} ) + ( \vec{a} ∧ \vec{c} ) $$

Altre proprietà del prodotto vettoriale

$$ k \cdot \vec{a} ∧ \vec{b} = \vec{a} ∧ k \cdot \vec{b} = k \cdot ( \vec{a} ∧ \vec{b} ) $$ $$ < \vec{a} , \vec{a} ∧ \vec{b} > = < \vec{b} , \vec{a} ∧ \vec{b} > = 0 $$ $$ || \vec{a} ∧ \vec{b} ||^2 = || \vec{a} ||^2 \cdot || \vec{b} ||^2 - < \vec{a} , \vec{b} >^2 $$ $$ || \vec{a} ∧ \vec{b} || = || \vec{a} || \cdot || \vec{b} || \cdot sin(\widehat{ \vec{a} , \vec{b} }) $$

Alle precedenti proprietà se ne aggiunge un'altra particolarmente utile per capire se i vettori sono paralleli.

Due vettori sono linearmente dipendenti se il loro prodotto vettoriale è nullo $$ \vec{a} ∧ \vec{b} = 0 \ \ \Rightarrow \ \ \vec{a} || \vec{b} $$

Il prodotto vettoriale è nullo nelle seguenti circostanze

• almeno uno dei due vettori è un vettore nullo $$ \vec{a} ∧ \vec{b} = 0 \ \ se \ \ \ \vec{a} = \vec{0} \ \ e/o \ \ \vec{b} = \vec{0} $$
• i due vettori sono paralleli o coincidenti, ossia linearmente dipendenti a||b $$ \vec{a} ∧ \vec{b} = 0 \ \ \Rightarrow \ \ \vec{a} || \vec{b} $$

Pertanto se nessuno dei due vettori è un vettori nullo, il prodotto vettoriale uguale a zero indica la dipendenza lineare dei vettori che sono paralleli o coincidenti tra loro.

Il prodotto vettoriale non soddisfa la proprietà associativa. La proprietà associativa non è soddisfatta dal prodotto vettoriale. Quindi, la sequenza dei prodotti vettoriali è molto importante. $$ \vec{a} \: ∧ \: ( \vec{b} \: ∧ \: \vec{c} ) \ne ( \vec{a} \: ∧ \: \vec{b} ) \: ∧ \: \vec{c} $$

 

Il doppio prodotto vettoriale

Il doppio prodotto vettoriale è un prodotto vettoriale in cui uno dei due fattori è a sua volta un prodotto vettoriale tra parentesi $$ \vec{a} \: ∧ \: ( \vec{b} \: ∧ \: \vec{c} ) $$

Uno dei due prodotti vettoriali è posto tra parentesi perché il prodotto vettoriale non gode della proprietà associativa.

$$ \vec{a} \: ∧ \: ( \vec{b} \: ∧ \: \vec{c} ) \ne ( \vec{a} \: ∧ \: \vec{b} ) \: ∧ \: \vec{c} $$

Nota. Per il doppio prodotto vettoriale vale l'identità del doppio prodotto vettoriale o formula di Lagrange secondo cui $$ \vec{a} \: ∧ \: ( \vec{b} \: ∧ \: \vec{c} ) = ( \vec{a} · \vec{c} ) · \vec{b} - ( \vec{a} · \vec{b} ) · \vec{c} $$ o alternativamente $$ \vec{a} \: ∧ \: ( \vec{b} \: ∧ \: \vec{c} ) = \vec{b} · ( \vec{a} · \vec{c} ) - \vec{c} · ( \vec{a} · \vec{b} ) $$ Da notare che nel membro di sinistra delle equazioni ci sono prodotti vettoriali mentre nel membro di destra ci sono prodotti scalari. L'identità resta comunque tra due vettori. Ad esempio nell'espressione (a·c)·b il prodotto scalare tra i due vettori (a·c) restituisce uno scalare α. Il prodotto esterno α·b è una moltiplicazione tra uno scalare (α) e un vettore (c), quindi il risultato finale è un altro vettore. Spesso la formula di Lagrange si ricorda in modo mnemonico come ACB-ABC oppure BAC-CAB. Per vedere un esempio pratico rimando agli appunti sull'identità del doppio prodotto vettoriale.

 

Esempio

Ho tre vettori

$$ \vec{a}=\begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} $$

$$ \vec{b}=\begin{pmatrix} 3 \\ 4 \\ 5 \end{pmatrix} $$

$$ \vec{c}=\begin{pmatrix} 6 \\ 7 \\ 8 \end{pmatrix} $$

Per calcolare il triplo prodotto vettoriale ax(bxc) svolgo prima il prodotto vettoriale tra parentesi (bxc)

$$ \vec{a} \: ∧ \: ( \vec{b} \: ∧ \: \vec{c} ) $$

$$ \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} \: ∧ \: (\begin{pmatrix} 3 \\ 4 \\ 5 \end{pmatrix} \: ∧ \: \begin{pmatrix} 6 \\ 7 \\ 8 \end{pmatrix} ) $$

$$ \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} \: ∧ \: \begin{pmatrix} det \begin{pmatrix} 4 & 7\\ 5 & 8 \end{pmatrix} \\ -det \begin{pmatrix} 3 & 6\\ 5 & 8 \end{pmatrix} \\ det \begin{pmatrix} 3 & 6\\ 4 & 7 \end{pmatrix} \end{pmatrix} $$

$$ \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} \: ∧ \: \begin{pmatrix} -3 \\ 6 \\ -3 \end{pmatrix} $$

Poi calcolo il prodotto vettoriale più esterno

$$ \begin{pmatrix} det \begin{pmatrix} 2 & 6\\ 3 & -3 \end{pmatrix} \\ -det \begin{pmatrix} 1 & -3\\ 3 & -3 \end{pmatrix} \\ det \begin{pmatrix} 1 & -3\\ 2 & 6 \end{pmatrix} \end{pmatrix} $$

$$ \begin{pmatrix} -24 \\ -6 \\ 12 \end{pmatrix} $$

Il prodotto vettoriale tra gli assi cartesiani

Il prodotto vettoriale tra gli assi cartesiani è il seguente

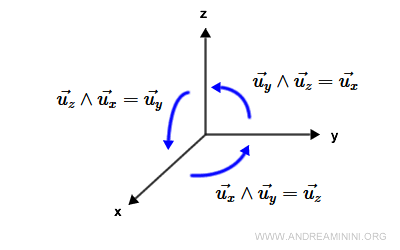
Considerando anche i versori opposti

$$ \vec{u_x} ∧ \vec{u_y} = \vec{u_z} $$

$$ \vec{u_y} ∧ \vec{u_x} = - \vec{u_z} $$

$$ \vec{u_y} ∧ \vec{u_z} = \vec{u_x} $$

$$ \vec{u_z} ∧ \vec{u_y} = - \vec{u_x} $$

$$ \vec{u_z} ∧ \vec{u_x} = \vec{u_y} $$

$$ \vec{u_x} ∧ \vec{u_z} = - \vec{u_y} $$

Il prodotto vettoriale tra un versore e se stesso è, invece, nullo.

$$ \vec{u_x} ∧ \vec{u_x} = \vec{0} $$

$$ \vec{u_y} ∧ \vec{u_y} = \vec{0} $$

$$ \vec{u_z} ∧ \vec{u_z} = \vec{0} $$

Una formula alternativa del prodotto vettoriale

Una formula alternativa per calcolare il prodotto vettoriale di due vettori nello spazio R³ è la seguente $$ \vec{a} ∧ \vec{b} = (a_y b_z - a_z b_y ) \vec{u_x} + (a_z b_x - a_x b_z) \vec{u_y} + ( a_x b_y - a_y b_x ) \vec{u_z} $$

E' una forma equivalente per ottenere il prodotto vettoriale.

E' particolarmente utile quando voglio calcolare il prodotto vettoriale usando le componenti dei vettori.

Come ricordare la formula? Questa formula non è facilissima da ricordare. Per fortuna, c'è un escamotage per costruirla rapidamente. Creo una tabella mettendo i versori (u) nella prima riga, il primo vettore (a) nella seconda riga e il secondo vettore (b) nella terza riga. $$ \begin{pmatrix} u_x & u_y & u_z \\ a_x & a_y & a_z \\ b_x & b_y & b_z \end{pmatrix} $$ Ora faccio finta che sia una matrice e svolgo il calcolo del determinante con la regola di Sarrus. $$ u_x a_y b_z + u_y a_z b_x + u_z a_x b_y - u_z a_y b_x - u_x a_z b_y - u_y a_x b_z $$ Poi metto in evidenza i versori $$ (a_y b_z - a_z b_y )u_x + ( a_z b_x - a_x b_z )u_y + (a_x b_y - a_y b_x )u_z $$ Ho così ricostruito la formula.

La dimostrazione

Prendo in considerazione un prodotto vettoriale tra due vettori nello spazio R³

$$ \vec{a} ∧ \vec{b} $$

Un vettore è uguale alla somma delle sue componenti x, y, z

$$ \vec{a} = a_x \vec{u_x} + a_y \vec{u_y} + a_z \vec{u_z} $$

$$ \vec{b} = b_x \vec{u_x} + b_y \vec{u_y} + b_z \vec{u_z} $$

Quindi, posso riscrivere il prodotto vettoriale in questa forma equivalente

$$ \vec{a} ∧ \vec{b} = ( a_x \vec{u_x} + a_y \vec{u_y} + a_z \vec{u_z} ) \ ∧ \ ( b_x \vec{u_x} + b_y \vec{u_y} + b_z \vec{u_z} ) $$

Per la proprietà distributiva rispetto alla somma

$$ a_x \vec{u_x} \ ∧ \ ( b_x \vec{u_x} + b_y \vec{u_y} + b_z \vec{u_z} ) + a_y \vec{u_y} \ ∧ \ ( b_x \vec{u_x} + b_y \vec{u_y} + b_z \vec{u_z} ) + a_z \vec{u_z} \ ∧ \ ( b_x \vec{u_x} + b_y \vec{u_y} + b_z \vec{u_z} ) = $$

e ancora per la proprietà distributiva rispetto alla somma

$$ a_x \vec{u_x} \ ∧ \ b_x \vec{u_x} + a_x \vec{u_x} \ ∧ \ b_y \vec{u_y} + a_x \vec{u_x} \ ∧ \ b_z \vec{u_z} + $$

$$ a_y \vec{u_y} \ ∧ \ b_x \vec{u_x} + a_y \vec{u_y} \ ∧ \ b_y \vec{u_y} + a_y \vec{u_y} \ ∧ \ b_z \vec{u_z} + $$

$$ a_z \vec{u_z} \ ∧ \ b_x \vec{u_x} + a_z \vec{u_z} \ ∧ \ b_y \vec{u_y} + a_z \vec{u_z} \ ∧ \ b_z \vec{u_z} = $$

Sapendo che il prodotto vettoriale tra u_x ∧ u_x = 0, u_y ∧ u_y = 0, u_z ∧ u_z = 0.

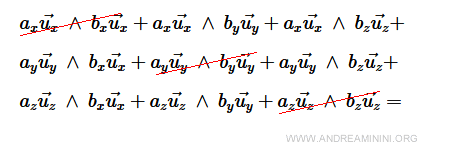
Dopo la semplificazione l'equazione diventa

$$ a_x \vec{u_x} \ ∧ \ b_y \vec{u_y} + a_x \vec{u_x} \ ∧ \ b_z \vec{u_z} + $$

$$ a_y \vec{u_y} \ ∧ \ b_x \vec{u_x} + a_y \vec{u_y} \ ∧ \ b_z \vec{u_z} + $$

$$ a_z \vec{u_z} \ ∧ \ b_x \vec{u_x} + a_z \vec{u_z} \ ∧ \ b_y \vec{u_y} = $$

che posso scrivere in una forma equivalente considerando che a_x, a_y, a_z, b_x, b_y, b_z sono scalari.

$$ a_x b_y ( \vec{u_x} \ ∧ \ \vec{u_y} ) + a_x b_z ( \vec{u_x} \ ∧ \ \vec{u_z} ) + $$

$$ a_y b_x ( \vec{u_y} \ ∧ \ \vec{u_x} ) + a_y b_z ( \vec{u_y} \ ∧ \ \vec{u_z} ) + $$

$$ a_z b_x ( \vec{u_z} \ ∧ \ \vec{u_x} ) + a_z b_y ( \vec{u_z} \ ∧ \ \vec{u_y} ) = $$

Sapendo che u_x ∧ u_y = u_z e u_y ∧ u_x = -u_z

$$ a_x b_y ( \vec{u_z} ) + a_x b_z ( \vec{u_x} \ ∧ \ \vec{u_z} ) + $$

$$ a_y b_x ( - \vec{u_z} ) + a_y b_z ( \vec{u_y} \ ∧ \ \vec{u_z} ) + $$

$$ a_z b_x ( \vec{u_z} \ ∧ \ \vec{u_x} ) + a_z b_y ( \vec{u_z} \ ∧ \ \vec{u_y} ) = $$

Sapendo che u_y ∧ u_z = u_x e u_z ∧ u_y = -u_x

$$ a_x b_y ( \vec{u_z} ) + a_x b_z ( \vec{u_x} \ ∧ \ \vec{u_z} ) + $$

$$ a_y b_x ( - \vec{u_z} ) + a_y b_z ( \vec{u_x} ) + $$

$$ a_z b_x ( \vec{u_z} \ ∧ \ \vec{u_x} ) + a_z b_y (- \vec{u_x} ) = $$

Sapendo che u_z ∧ u_x = u_y e u_x ∧ u_z = -u_y

$$ a_x b_y ( \vec{u_z} ) + a_x b_z ( - \vec{u_y} ) + $$

$$ a_y b_x ( - \vec{u_z} ) + a_y b_z ( \vec{u_x} ) + $$

$$ a_z b_x ( \vec{u_y} ) + a_z b_y (- \vec{u_x} ) = $$

Quindi ottengo

$$ a_x b_y \vec{u_z} - a_x b_z \vec{u_y} - a_y b_x \vec{u_z} + a_y b_z \vec{u_x} + a_z b_x \vec{u_y} - a_z b_y \vec{u_x} = $$

Metto in evidenza i versori

$$ (a_y b_z - a_z b_y ) \vec{u_x} + ( a_z b_x - a_x b_z ) \vec{u_y} + ( a_x b_y - a_y b_x ) \vec{u_z} $$

E la formula è dimostrata

E così via.