I vettori paralleli

Due vettori del piano sono detti paralleli se sono linearmente dipendenti.

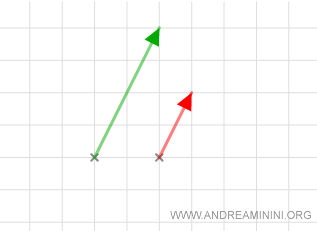
Un esempio pratico

Dati due vettori v₁ e v₂ dello spazio vettoriale V=R² nel campo K=R

$$ v_1 = \overrightarrow{AB} = ( 2,4 ) \\ v_2 = \overrightarrow{CD} = ( 1,2 ) $$

I due vettori sono linearmente dipendenti se il determinante della matrice composta dai due vettori colonna è uguale a zero.

$$ det \begin{pmatrix} 2 & 1 \\ 4 & 2 \end{pmatrix} = 0 $$

Ciò equivale a dire che i due vettori sono proporzionali tra loro.

Nota. In questo caso il vettore AB è il doppio del vettore CD. $$ \overrightarrow{CD} = 2 \cdot \overrightarrow{AB} = 2 \cdot \begin{pmatrix} 1 \\ 2 \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \end{pmatrix} $$

Il rango della matrice dei vettori colonna è uguale o minore di uno.

$$ rg \begin{pmatrix} 2 & 1 \\ 4 & 2 \end{pmatrix} \le 1 $$

Dimostrazione

Rappresento graficamente entrambi i vettori a partire dall'origine O(0,0 )

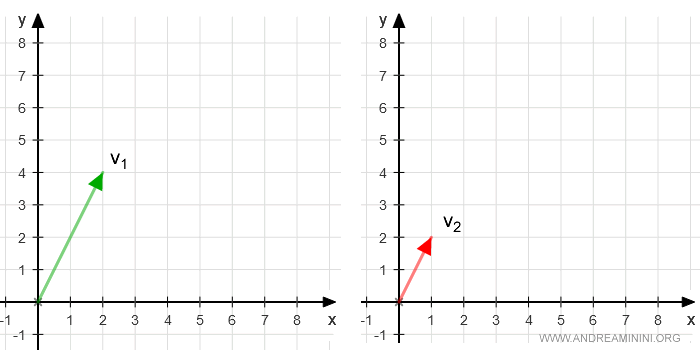
E' subito evidente che i due vettori sono proporzionali, perché si trovano sulla stessa retta passante per l'origine.

Un vettore è un multiplo dell'altro. Esiste un numero scalare k tale che v₁=k·v₂.

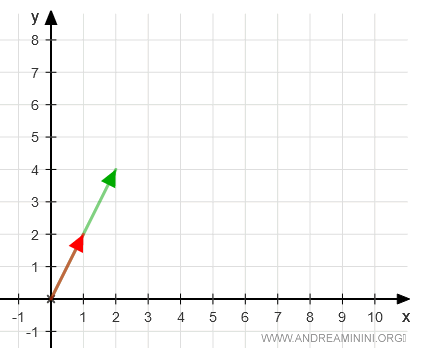
Ho così dimostrato la dipendenza lineare dei due vettori.

E così via.

Corollari

• Vettore parallelo a una retta

  Un vettore è parallelo a una retta r del piano se giace su una retta parallela alla retta r oppure sulla retta r stessa.

• Vettore applicato a un punto

  Qualsiasi punto P del piano genera un vettore applicato PP parallelo a ogni retta del piano.

Vettori paralleli nello spazio

In uno spazio a tre dimensioni R³

Un vettore è parallelo a una retta se ha lo stesso vettore direttore o lo stesso vettore normale.

$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \\ z_0 \end{pmatrix} + t \cdot \begin{pmatrix} l \\ m \\ n \end{pmatrix} $$

Dove (l,m,n) è il vettore direttore dell'equazione vettoriale mentre (x₀,y₀,z₀) è un punto qualsiasi della retta.

Un vettore direttore individua la direzione di tutte le rette parallele al vettore stesso.

Un vettore è parallelo a un piano se giace su un piano parallelo.