Vettore opposto

Il vettore opposto di $ \vec{v} $ è un vettore $ -\vec{v} $ caratterizzato da stessa direzione e modulo (lunghezza) ma verso opposto.

Per trovare il vettore opposto basta moltiplicare il vettore v per lo scalare -1 tramite l'operazione di prodotto di un vettore per uno scalare (numero).

Un esempio pratico

Prendo in considerazione un vettore con modulo 3.

La retta in cui si trova il vettore è la direzione mentre la lunghezza (modulo) è pari a 3.

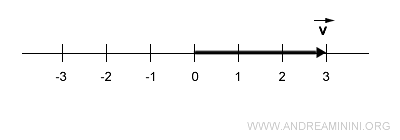
Il vettore opposto è un vettore lungo la stessa retta (direzione) e con uguale lunghezza (3) ma verso opposto.

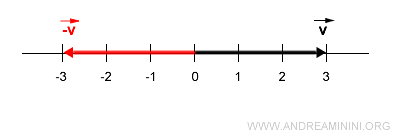
Esempio 2

Ora considero un vettore in uno spazio a due dimensioni

$$ \vec{v} = \begin{pmatrix} 1 \\ 2 \end{pmatrix} $$

In un diagramma cartesiano il vettore congiunge l'origine O con il punto alle coordinate (1,2).

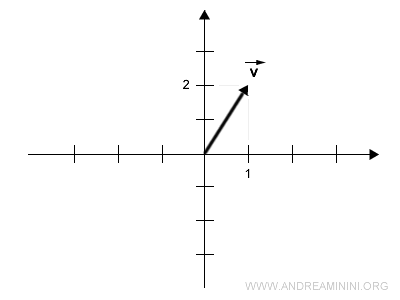
Per calcolare il vettore opposto calcolo il prodotto del vettore v per lo scalare -1.

$$ - \vec{v} = -1 \cdot \vec{v} $$

$$ - \vec{v} = -1 \cdot \begin{pmatrix} 1 \\ 2 \end{pmatrix} $$

$$ - \vec{v} = \begin{pmatrix} -1 \cdot 1 \\ -1 \cdot 2 \end{pmatrix} $$

$$ - \vec{v} = \begin{pmatrix} -1 \\ -2 \end{pmatrix} $$

Il vettore opposto congiunge l'origine con il punto alle coordinate (-1,-2).

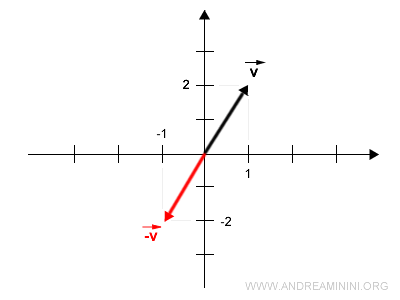
Note a margine

Alcune osservazioni personali e note a margine sui vettori opposti

• La somma di due vettori opposti è sempre uguale al vettore nullo
  Se \( \vec{v} \) è un vettore in uno spazio vettoriale \( V \), il suo opposto, indicato con \( -\vec{v} \), è definito come il vettore che, sommato a \( \vec{v} \), restituisce il vettore nullo. $$ \vec{v} + (-\vec{v}) = \vec{0} $$ Questa proprietà deriva direttamente dalla definizione di opposto di un vettore e dall'associatività e commutatività della somma nello spazio vettoriale.

  Esempio. Considero il vettore $ \vec{v} $ nello spazio vettoriale $ \mathbb{R}^2 $. $$ \vec{v} = \begin{pmatrix} 3 \\ -2 \end{pmatrix} $$ Il suo opposto \( -\vec{v} \) è il vettore: $$ -\vec{v} = \begin{pmatrix} -3 \\ 2 \end{pmatrix} $$ Calcolo la somma di \( \vec{v} \) e \( -\vec{v} \) $$ \vec{v} + (-\vec{v}) = \begin{pmatrix} 3 \\ -2 \end{pmatrix} + \begin{pmatrix} -3 \\ 2 \end{pmatrix} = \begin{pmatrix} 3 + (-3) \\ -2 + 2 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} $$ Il risultato è il vettore nullo \( \vec{0} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} \).

E così via.