La somma di due vettori

Dati due vettori qualsiasi v e w, la somma dei vettori v+w si può calcolare con il metodo del parallelogramma o la somma algebrica delle coordinate dei vettori. $$ \vec{v} + \vec{w} = \begin{pmatrix} v_1 \\ v_2 \\ \vdots \\ v_n \end{pmatrix} + \begin{pmatrix} w_1 \\ w_2 \\ \vdots \\ w_n \end{pmatrix} = \begin{pmatrix} v_1 + w_1 \\ v_2 + w_2 \\ \vdots \\ v_n + w_n \end{pmatrix} $$

In entrambi i casi l'addizione dei vettori v+w è un altro vettore.

E' detto vettore somma.

Il metodo del parallelogramma

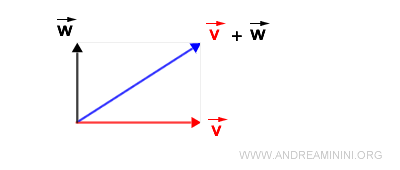
Il metodo del parallelogramma mi permette di sommare i due vettori sul piano tramite un'operazione geometrica.

I vettori v e w hanno la stessa origine (O) e una direzione diversa.

• La lunghezza del vettore v è un segmento dal punto O al punto A.
• La lunghezza del vettore w è un segmento s dal punto O al punto B.

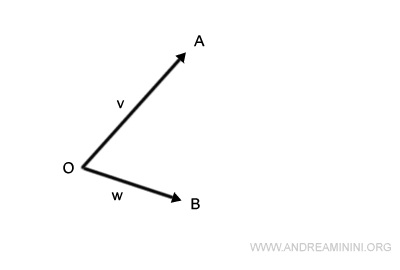
A questo punto traslo il segmento OA per farlo passare da B.

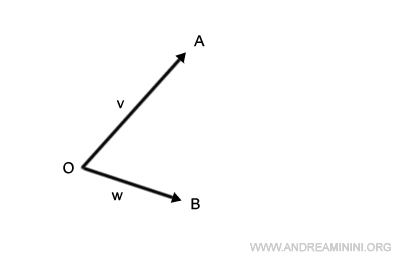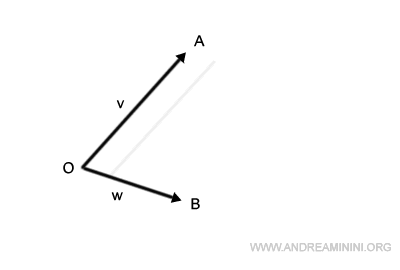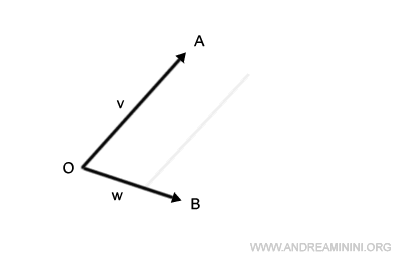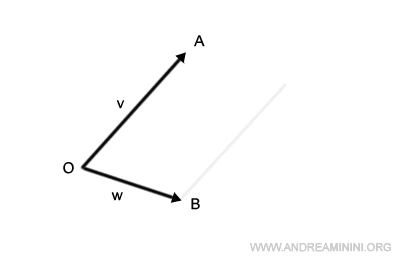
Faccio lo stesso con il segmento OB, lo traslo per farlo passare da A.

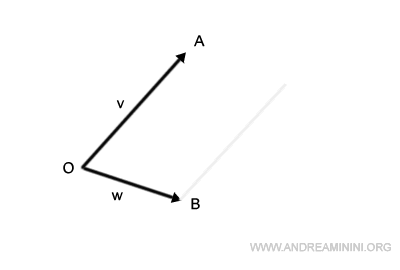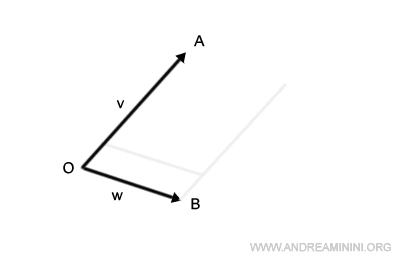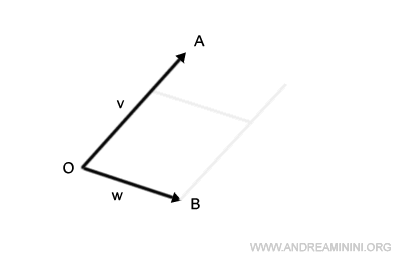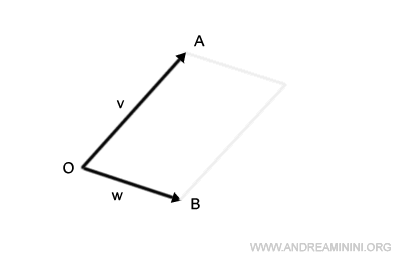
L'intersezione dei segmenti appena traslati individua un punto C.

In questo modo ottengo un parallelogramma OACB.

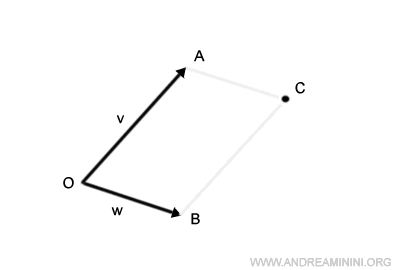
Il segmento che unisce l'origine O con il punto C è il vettore somma v+w.

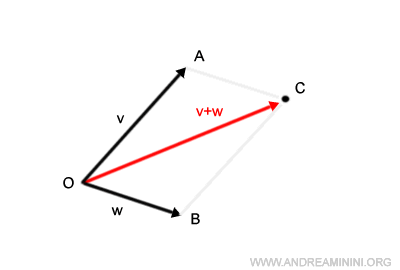
Nota. Se due vettori hanno la stessa direzione, i due moduli si collocano su una stessa retta. In questo caso il metodo del parallelogramma non può essere usato perché formano un parallelogramma degenere. E' però possibile usare il metodo del punto medio.

Un esempio di calcolo

Ho due vettori nello spazio V=R² .

$$ P_1 \begin{pmatrix} x_1 \\ y_1 \end{pmatrix} = \begin{pmatrix} 1 \\ 2 \end{pmatrix} $$ $$ P_2 \begin{pmatrix} x_2 \\ y_2 \end{pmatrix} = \begin{pmatrix} 3 \\ 1 \end{pmatrix}$$

Li rappresento sul piano a due dimensioni (x,y) tramite due segmenti orientati OP₁ e OP₂ che congiungono rispettivamente l'origine con i punti P₁ e P₂.

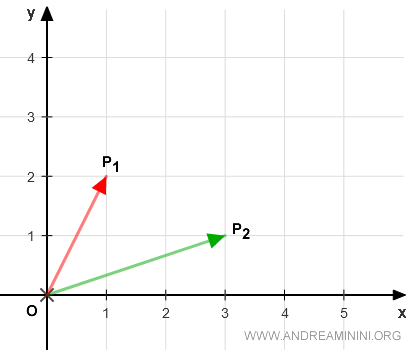
Nota. Ogni punto del piano identifica un vettore passante per l'origine. E viceversa, ogni punto del piano indica un vettore che parte dall'origine O. Quindi, i punti del piano (x,y) e i vettori sono equivalenti.

Per calcolare la somma dei due vettori OP₁ e OP₂ uso il metodo del parallelogramma.

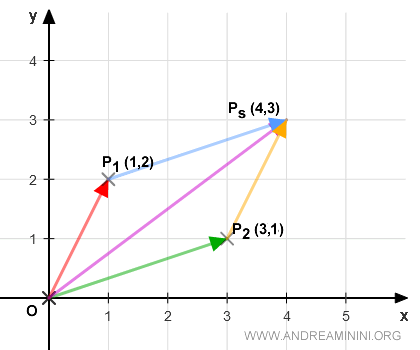
Il vettore somma OP₁+OP2 congiunge l'origine con il punto Ps(4,3).

Il metodo punta-coda

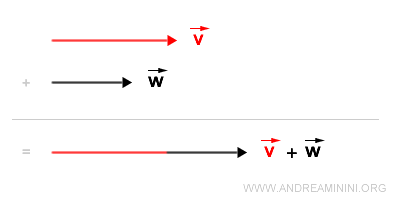
In alternativa posso semplicemente traslare uno dei due vettori facendo coincidere il suo punto di applicazione (origine della freccia) con l'estremo dell'altro vettore.

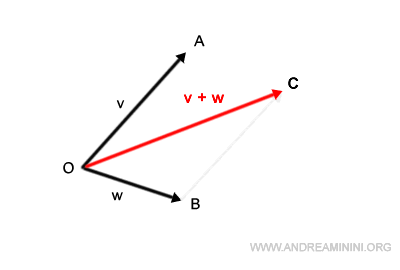
In questo modo ottengo le coordinate dell'estremo del vettore somma v+w.

Esempio

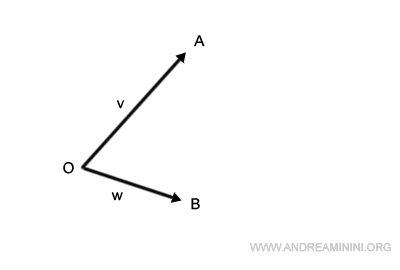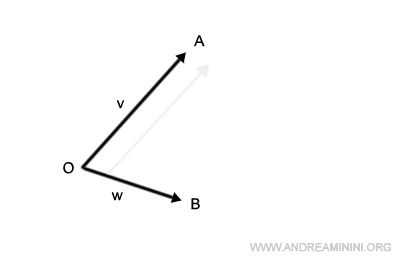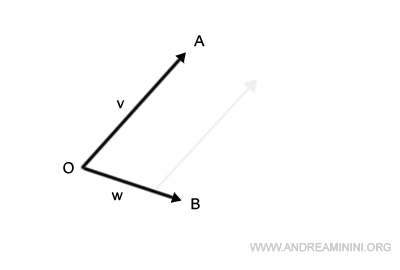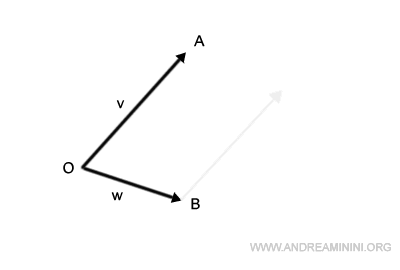
Devo calcolare la somma tra i vettori v e w.

Sposto l'origine del vettore v sull'estremo del vettore w.

Poi congiungo l'origine O con l'estremo del vettore v traslato e ottengo il vettore somma v+w.

Il risultato finale è lo stesso che ho già ottenuto col metodo del parallelogramma.

Tuttavia, questo metodo è più rapido e mi permette anche di sommare più vettori tra loro in modo ricorsivo.

Esempio

Devo calcolare la somma di tre i vettori v, w, z.

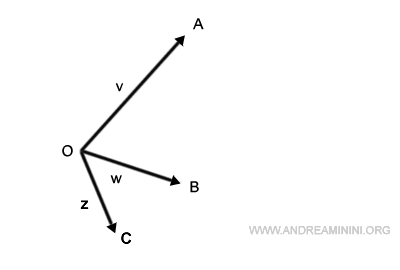
Sposto l'origine del vettore w sull'estremo del vettore v.

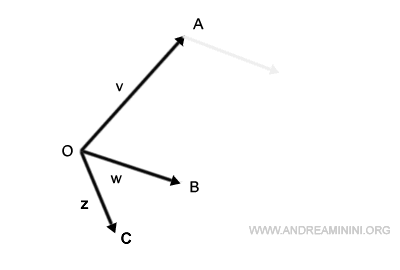
Poi sposto l'origine del vettore z in coda al vettore w'.

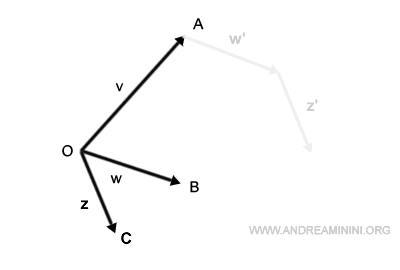
Congiungo l'origine con questo punto e ottengo il vettore somma v+w+z.

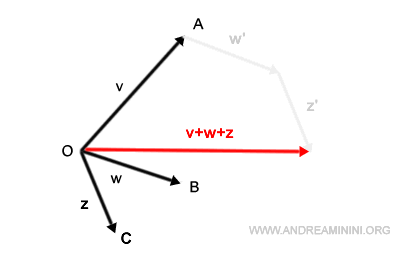
E' un metodo utile per sommare geometricamente più vettori tra loro.

Nota. Non è importante quale sequenza scelgo per concatenare i vettori. Il risultato finale è sempre lo stesso. Ad esempio, sposto l'origine del vettore v sull'estremo del vettore w, poi sposto il vettore z in coda. Il vettore somma v+w+z è comunque lo stesso.

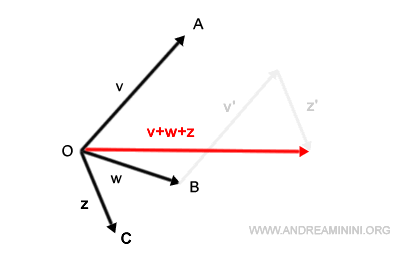
La somma algebrica dei vettori

Per calcolare il vettore somma posso anche sommare tra loro le coordinate (x,y) dei due vettori.$$ \begin{pmatrix} x_1 \\ y_1 \end{pmatrix} + \begin{pmatrix} x_2 \\ y_2 \end{pmatrix} = \begin{pmatrix} x_1+x_2 \\ y_1+y_2 \end{pmatrix} $$

La somma algebrica è utile perché si può applicare anche per vettori con più di due componenti.

Esempio

Riprendo i due vettori dell'esempio precedente

$$ P_1 = \begin{pmatrix} x_1 \\ y_1 \end{pmatrix} = \begin{pmatrix} 1 \\ 2 \end{pmatrix} $$ $$ P_2 = \begin{pmatrix} x_2 \\ y_2 \end{pmatrix} = \begin{pmatrix} 3 \\ 1 \end{pmatrix}$$

Poi calcolo la somma algebrica dei due vettori OP₁ e OP₂:

Per calcolare la somma algebrica basta sommare tra loro le coordinate x e y dei due vettori.

$$ OP_S = OP_1 + OP_2 = \begin{pmatrix} 1 \\ 2 \end{pmatrix} + \begin{pmatrix} 3 \\ 1 \end{pmatrix} = \begin{pmatrix} 4 \\ 3 \end{pmatrix} $$

Ciò che ottengo è il vettore somma.

Ora rappresento il nuovo vettore sul piano cartesiano.

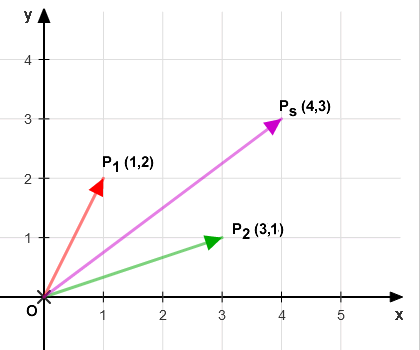
Nota. Il punto Ps è lo stesso vettore somma che ho ottenuto usando il metodo del parallelogramma. Il risultato è lo stesso.

Esempio 2

Ho due vettori nello spazio a tre dimensioni (x, y, z)

$$ P_1= \begin{pmatrix} x_1 \\ y_1 \\ z_1 \end{pmatrix} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} $$ $$ P_2 = \begin{pmatrix} x_2 \\ y_2 \\ z_2 \end{pmatrix} = \begin{pmatrix} 3 \\ 1 \\ 4 \end{pmatrix}$$

Il vettore somma è un vettore composto dalla somma delle componenti x, y, z

$$ P_1 + P_2 = \begin{pmatrix} x_1 \\ y_1 \\ z_1 \end{pmatrix} + \begin{pmatrix} x_2 \\ y_2 \\ z_2 \end{pmatrix} = \begin{pmatrix} x_1 + x_2 \\ y_1 + y_2 \\ z_1 + z_2 \end{pmatrix} = \begin{pmatrix} 1 + 3 \\ 2 + 1 \\ 3 + 4 \end{pmatrix} = \begin{pmatrix} 4 \\ 3 \\ 7 \end{pmatrix} $$

Lo stesso metodo posso applicarlo per sommare vettori di qualsiasi dimensione.

Esempio 3

Ho due vettori nello spazio a quattro dimensioni (x₁, x₂, x₃, x₄)

$$ v = \begin{pmatrix} 1 \\ 2 \\ 3 \\ 4 \end{pmatrix} $$ $$ w = \begin{pmatrix} 3 \\ 1 \\ 4 \\ -2 \end{pmatrix}$$

Il vettore somma è un vettore composto dalla somma delle componenti dei vettori

$$ v + w = \begin{pmatrix} 1 \\ 2 \\ 3 \\ 4 \end{pmatrix} + \begin{pmatrix} 3 \\ 1 \\ 4 \\ -2 \end{pmatrix} = \begin{pmatrix} 1+3 \\ 2+1 \\ 3+4 \\ 4+(-2) \end{pmatrix} = \begin{pmatrix} 4 \\ 3 \\ 7 \\ 2 \end{pmatrix} $$

Lo stesso metodo posso usarlo per sommare tre o più vettori tra loro.

Esempio 3

Ho tre vettori nello spazio a quattro dimensioni (x₁, x₂, x₃, x₄)

$$ v_1 = \begin{pmatrix} 1 \\ 2 \\ 3 \\ 4 \end{pmatrix} $$ $$ v_2 = \begin{pmatrix} 3 \\ 1 \\ 4 \\ -2 \end{pmatrix}$$ $$ v_3 = \begin{pmatrix} -1 \\ 1 \\ 1 \\ 3 \end{pmatrix} $$

Il vettore somma è un vettore composto dalla somma delle componenti dei vettori

$$ v_1 + v_2 + v_3 = \begin{pmatrix} 1 \\ 2 \\ 3 \\ 4 \end{pmatrix} + \begin{pmatrix} 3 \\ 1 \\ 4 \\ 3 \end{pmatrix} + \begin{pmatrix} -1 \\ 1 \\ 1 \\ -2 \end{pmatrix} = \begin{pmatrix} 1+3 +(-1) \\ 2+1+1 \\ 3+4+1 \\ 4+(-2)+3 \end{pmatrix} = \begin{pmatrix} 3 \\ 4 \\ 8 \\ 5 \end{pmatrix} $$

E via dicendo

Il metodo del punto medio

Per calcolare la somma di due vettori allineati su una stessa direzione, trovo il punto medio M tra i due vertici e moltiplico per due il segmento OM.

Il metodo del punto medio permette di sommare geometricamente due vettori anche se sono allineati ossia hanno la stessa direzione e verso opposto.

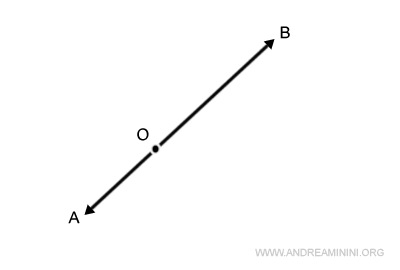
Nota. Se i vettori sono allineati con verso opposto non posso usare il metodo del parallelogramma perché i vettori formano un parallelogramma degenere. In questo caso è utile usare il metodo del punto medio. Se invece i vettori sono allineati ma hanno lo stesso verso, si tratta di un caso banale perché è sufficiente sommare i due moduli o prolungare geometricamente il primo sul secondo (o viceversa).

Dimostrazione

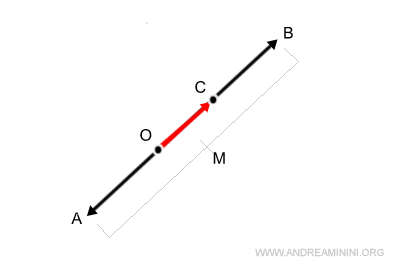
In un parallelogramma le diagonali si intersecano nel punto medio di due vertici opposti.

Sapendo che il segmento OC è il modulo del vettore somma v+w, traccio una seconda diagonale (AB) sul parallelogramma per trovare il punto medio M.

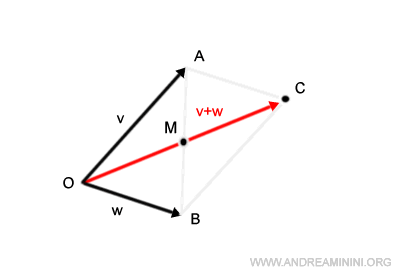
Il punto medio M ha due caratteristiche geometriche molto utili:

1. Il punto medio M ha la stessa distanza rispetto al punto O e al punto C $$ OM=MC $$
2. Il segmento OM è la metà del modulo del vettore somma (OC) $$ OC = 2 \cdot OM $$

Posso applicare queste considerazioni per calcolare il vettore somma di due vettori aventi la stessa direzione.

Calcolo il punto medio tra i due vertici opposti A e B.

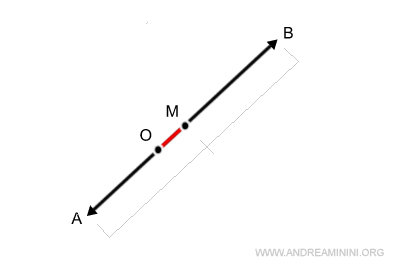
In questo modo ottengo un segmento OM.

Sapendo che OM è la metà della lunghezza del vettore somma, moltiplico per due il segmento 2 OM.

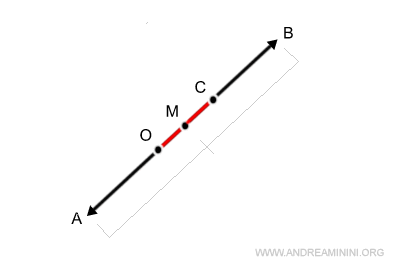
Ho così trovato il modulo del vettore somma dei due vettori.

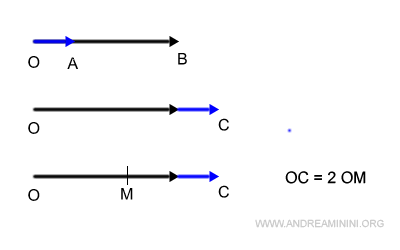
Nota. Il metodo del punto medio è applicabile anche se i vettori sono allineati e hanno lo stesso verso. Questo caso è però banale. Per calcolare il punto medio M devo sommare le lunghezze dei due vettori, dividere la somma per due per trovare il punto medio M e moltiplicare per due il punto medio M per ottenere il vettore somma. Queste ultime due operazioni sono ridondanti. Se i vettori hanno lo stesso verso è sufficiente sommare le due lunghezze dei vettori senza calcolare il punto medio.

La diseguaglianza triangolare

Il modulo (norma) della somma di due vettori è minore o uguale alla somma dei moduli dei due vettori. $$ | \vec{v} + \vec{w} | \le |\vec{v}|+|\vec{w}| $$

Questo spiega la diseguaglianza triangolare.

Si chiama diseguaglianza triangolare perché si verifica in tutti i triangoli.

In qualsiasi triangolo la somma di due lati è sempre maggiore alla lunghezza del lato restante.

Il caso di uguaglianza tra il modulo della somma e la somma dei moduli dei vettori si verifica solo quando i vettori sono paralleli o coincidenti e hanno lo stesso verso.

$$ | \vec{v} + \vec{w} | = |\vec{v}|+|\vec{w}| $$

In quest'ultimo caso la somma dei vettori ha la stessa direzione e verso dei due vettori.

E così via.