Campo vettoriale

Cos'è un campo vettoriale

Un campo vettoriale è una funzione F che associa un vettore a ogni punto di uno spazio. $$ \vec{v} = F(x,y,z) $$

In altre parole, a ogni punto dello spazio a tre dimensioni (xyz) sono associati tre quantità scalari che rappresentano quanto il vettore punta lungo ciascun asse x, y e z.

Nello spazio a due dimensioni (xy), invece, a ogni punto sono associati due quantità scalari, ossia le componenti del vettore associato al punto lungo gli assi x e y.

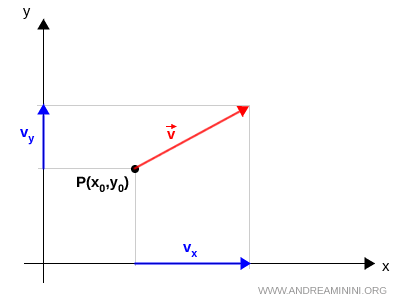
I vettori associati ai punti sono uguali o diversi tra loro?

In un campo vettoriale i vettori possono avere direzione, verso e modulo diversi oppure uguali.

Ecco un esempio pratico di campo vettoriale in una regione del piano (spazio a due dimensioni).

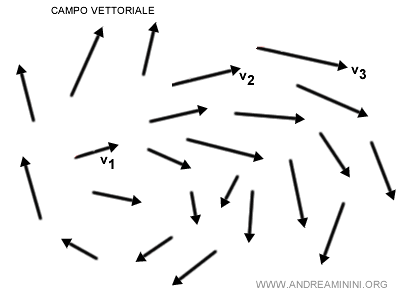
Esempio. Il vento su una mappa meteorologica. Ogni punto della mappa ha una freccia che indica da dove soffia il vento e quanto forte. Questo è un campo vettoriale.

Se i vettori sono uguali, il campo vettoriale è detto campo vettoriale costante.

Ad esempio, la forza di gravità in prossimità della superficie terrestre.

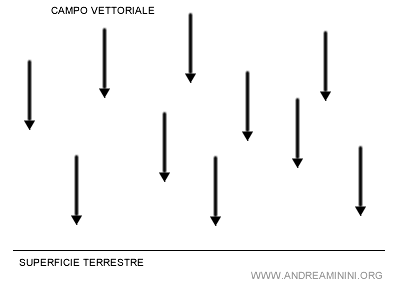
E' possibile definire un campo vettoriale anche nello spazio euclideo a tre dimensioni.

Ad esempio, la direzione, il verso e l'intensità dei flussi d'aria intorno a una sfera.

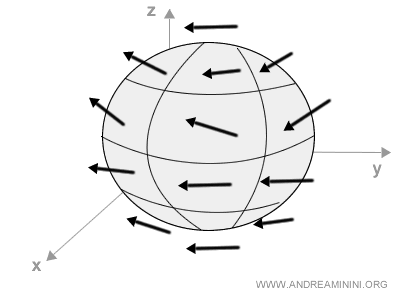
In questo caso ogni vettore ha tre componenti che rappresentano la proiezione del vettore sull'asse x, y e z.

$\vec{v}(x, y, z) = \begin{pmatrix} v_x(x,y,z) \\ v_y(x,y,z) \\ v_z(x,y,z) \end{pmatrix}$

In generale un campo vettoriale può anche variare nel tempo: in quel caso si aggiunge un quarto elemento a indicare il tempo $ F(x, y, z, t) $.

Un esempio pratico

Considero un campo vettoriale definito come:

$\vec{v}(x,y,z) = (2x,\ -y,\ 3z)$

Quali sono le quantità scalari associate al punto $(1,2,3)$?

Le coordinate del punto nello spazio sono

$$(x_0, y_0, z_0) = (1,2,3)$$

Sostituisco le coordinate nel punto nella funzione che definisce il campo vettoriale.

$$ \vec{v}(1,2,3) = (2 \cdot 1,\ -2,\ 3 \cdot 3)$$

$$ \vec{v}(1,2,3) = (2, -2,9)$$

Le componenti del vettore, cioè le quantità scalari che descrivono il vettore nel punto $(1,2,3)$, sono:

$$v_x = 2 $$

$$ v_y = -2 $$

$$ v_z = 9 $$

Quindi:

$\vec{v}(1,2,3) = (2,\ -2,\ 9)$

Questo significa che nel punto $ (1,2,3) $ è applicato un vettore con componenti $ +2 $ lungo l'asse x, $ -2 $ lungo l'asse y e $ +9 $ lungo l'asse z.

Graficamente, il vettore può essere rappresentato come una freccia che parte dal punto $ (1,2,3) $ e punta verso il punto $ (3,0,12) $, che corrisponde alla somma delle coordinate del punto e delle componenti del vettore.

$$ (1,2,3)+(2,-2,9)=(1+2, 2-2, 3+9) = (3,0,12) $$

Ecco come appare nello spazio 3D

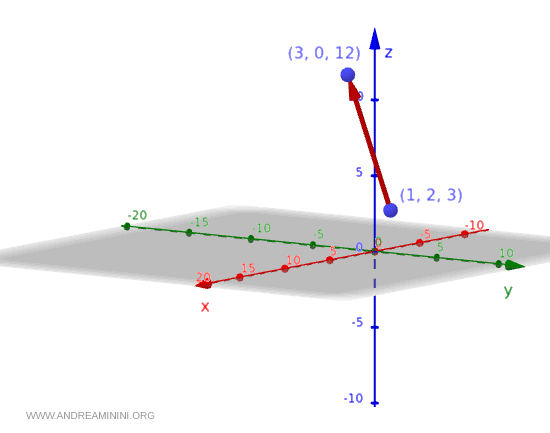
Lo stesso calcolo va ripetuto su tutti i punti dello spazio del campo vettoriale.

Nota. In quest'ultima ra  ppresentazione i vettori sono stati normalizzati, cioè vengono mostrati con la stessa lunghezza grafica, per renderli più leggibili. La direzione è corretta, ma la lunghezza disegnata non rappresenta il vero modulo del vettore.

La differenza tra campo vettoriale e spazio vettoriale

La classica confusione tra campo vettoriale e spazio vettoriale è un errore comune per chi inizia.

Si tratta di due concetti distinti.

• Spazio vettoriale
  Uno spazio vettoriale (o spazio lineare) è un insieme di oggetti chiamati "vettori" che posso sommare o moltiplicare per uno scalare (numeri, presi da un campo, come ℝ o ℂ) e soddisfano determinate regole. Gli oggetti possono anche non essere vettori. Ad esempio, esistono spazi vettoriali di matrici. Si tratta di un concetto astratto, una struttura matematica.
• Campo vettoriale
  In matematica un campo vettoriale è, invece, una funzione che a ogni punto di uno spazio (tipicamente ℝ² o ℝ³) associa un vettore. In fisica un campo vettoriale può esistere anche senza una funzione matematica generale che lo governi: basta che a ogni punto corrisponda un vettore (es. la mappa meteorologica che descrive il vento in una regione).

E così via.