Prodotto di un vettore per uno scalare
Il prodotto di uno scalare k per un vettore v si ottiene moltiplicando le n componenti del vettore per lo scalare. $$ k \cdot \vec{v} = k \cdot \begin{pmatrix} v_1 \\ v_2 \\ \vdots \\ \ v_n \end{pmatrix} = \begin{pmatrix} k \cdot v_1 \\ k \cdot v_2 \\ \vdots \\ \ k \cdot v_n \end{pmatrix} $$
Dove per scalare intendo un numero.
Il prodotto di un vettore v per uno scalare k è un vettore w=k·v che ha
- la stessa direzione del vettore v.
- una lunghezza (modulo) pari a |k|·v
- il verso è concorde se k>0 o discorde se k<0
Nota. Se lo scalare è zero k=0 il risultato del prodotto del vettore per lo scalare è un vettore nullo. Se k=1 il risultato è lo stesso vettore v. Se k=-1, invece, il risultato è il vettore opposto -v.
Un esempio pratico
Nello spazio a tre dimensioni (x,y,z) considero il vettore v
$$ \vec{v} = \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 3 \\ 1 \\ -2 \end{pmatrix} $$
Moltiplico il vettore per lo scalare k=2
$$ k \cdot \vec{v} = 2 \cdot \begin{pmatrix} 3 \\ 1 \\ -2 \end{pmatrix} $$
Il prodotto del vettore per lo scalare equivale a moltiplicare ogni componente del vettore per k = 2
$$ k \cdot \vec{v} = 2 \cdot \begin{pmatrix} 3 \\ 1 \\ -2 \end{pmatrix} = \begin{pmatrix} 2 \cdot 3 \\ 2 \cdot 1 \\ 2 \cdot (-2) \end{pmatrix} = \begin{pmatrix} 6 \\ 2 \\ -4 \end{pmatrix} $$
Il risultato finale è un altro vettore.
Esempio 2
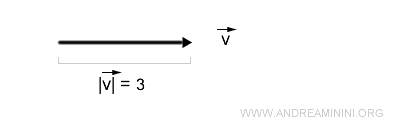
Prendo in considerazione il vettore v.
Il vettore ha una lunghezza (modulo) pari a |v|=3.
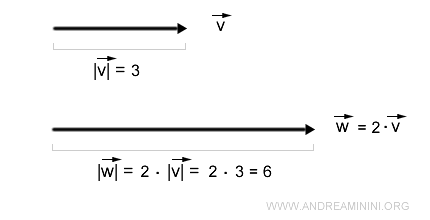
Il prodotto del vettore per lo scalare k=2
$$ \vec{w} = |k| \cdot \vec{v} $$
è un vettore w che la stessa direzione e verso ma modulo pari a 6.
$$ | \vec{w} | = |k| \cdot | \vec{v} | = 2 \cdot 3 = 6 $$
Ecco la rappresentazione grafica
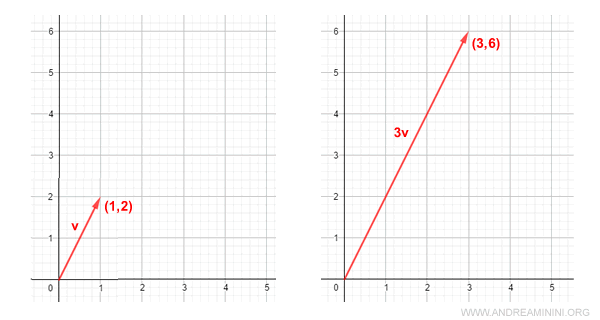
Nota. Dal punto di vista algebrico il prodotto di un vettore per uno scalare k è un vettore con tutti gli elementi moltiplicati per k. Ad esempio se k=3 e v=(1,2)^T. $$ k \cdot \vec{v} = 3 \cdot \begin{pmatrix} 1 \\ 2 \end{pmatrix} = \begin{pmatrix} 3 \cdot 1 \\ 3 \cdot 2 \end{pmatrix} = \begin{pmatrix} 3 \\ 6 \end{pmatrix} $$ Ecco la rappresentazione grafica.
Esempio 3
Prendo in considerazione il vettore v con modulo pari a |v|=3.

Quando k è un numero negativo, ad esempio k=-2, il prodotto del vettore v per lo scalare k=-2 è un vettore w che ha la stessa direzione ma verso opposto e modulo uguale a |w|=6.
$$ | \vec{w} | = |k| \cdot | \vec{v} | = |-2| \cdot 3 = 6 $$
Ecco la rappresentazione grafica
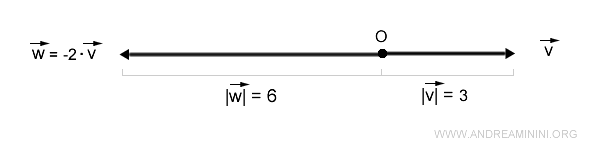
Nota. Se lo scalare fosse k=-1 otterrei il vettore opposto di v ossia un vettore -v con uguale direzione e modulo ma verso opposto rispetto a v.
e così via.
