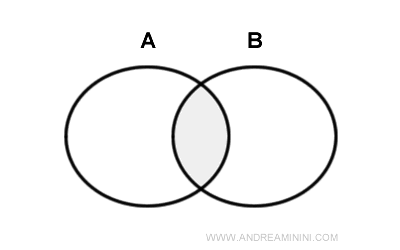
L'intersezione tra insiemi

L'intersezione tra due insiemi A e B è l'insieme degli elementi che appartengono sia all'insieme A che all'insieme B.

Il simbolo dell'intersezione è ⋂.

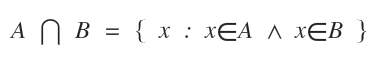
Quest'ultima scrittura si legge "intersezione di A e B" oppure "A intersecato a B"

Intersezione di più insiemi. Quando gli insiemi intersecati sono più di due, si può usare questa notazione più sintetica per indicare l'intersezione $$ \bigcap_{i \in I} = \{ x \in A_i \:\: \forall i \in I \} $$

Quando due insiemi non hanno elementi in comune, l'intersezione A⋂B è un insieme vuoto.

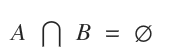
In questo caso i due insiemi sono detti insiemi disgiunti.

Un esempio pratico

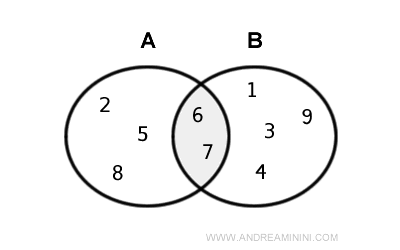
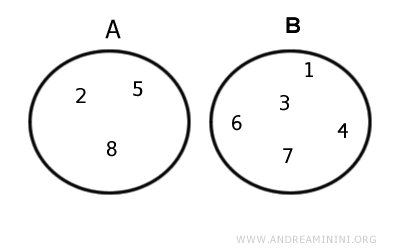
Considero due insiemi finiti A e B

$$ A = \{ 2,5,6,7, 8 \} $$

$$ B = \{ 1,3,4,6, 7,9 \} $$

I due insiemi hanno in comune due elementi.

$$ A = \{ 2,5, \color{red}6,\color{red}7, 8 \} $$

$$ B = \{ 1,3,4,\color{red}6, \color{red}7,9 \} $$

Pertanto, l'intersezione tra i due insiemi A⋂B è un insieme composto da due elementi (6,7).

$$ A \cap B = \{ 6,7 \} $$

Ecco la rappresentazione dell'intersezione con i diagrammi di Eulero-Venn

Tipi di intersezione

L'intersezione tra due insiemi A e B può avere diversi esiti

• L'intersezione A⋂B è un sottoinsieme proprio di entrambi gli insiemi.

  Esempio. Dati due insiemi $$ A = \{ 2,5,6,7, 8 \} $$ $$ B = \{ 1,3,4,6, 7,9 \} $$ La loro intersezione è $$ A \cap B = \{ 6,7 \} $$ In questo caso l'intersezione è un sottoinsieme proprio sia di A che di B $$ A \cap B ⊂ A $$ $$ A \cap B ⊂ B $$ E' l'esempio già visto in precedenza
  

• L'intersezione A⋂B è un sottoinsieme proprio di uno dei due insiemi e un sottoinsieme improprio dell'altro insieme. Questo accade se uno dei due insiemi è un sottoinsieme proprio dell'altro insieme. Ad esempio A⊂B.

  Esempio. Dati due insiemi $$ A = \{ 3,6,7 \} $$ $$ B = \{ 1,3,4,6, 7,9 \} $$ La loro intersezione è $$ A \cap B = \{ 3, 6,7 \} $$ Dal punto di vista grafico
  
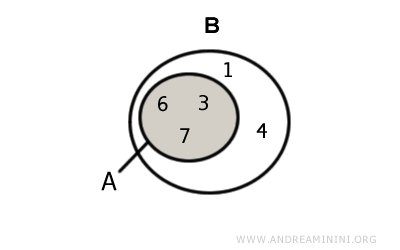
  In questo caso l'intersezione è un sottoinsieme improprio di A perché coincide con A $$ A \cap B = A $$ e un sottoinsieme proprio di B perché esiste almeno un elemento di B che non appartiene ad A $$ A \cap B ⊂ B $$

• L'intersezione A⋂B è un sottoinsieme improprio di entrambi gli insiemi. Questo accade in due diverse situazioni.
  
  A] Quando gli insiemi sono insiemi disgiunti l'intersezione è un insieme vuoto che per definizione è un sottoinsieme improprio di ogni insieme.
  

  Esempio. Dati due insiemi $$ A = \{ 2,5,8 \} $$ $$ B = \{ 1,3,4,6, 7,9 \} $$ La loro intersezione è un insieme vuoto $$ A \cap B = \{ \ \ \} = Ø $$ In questo caso i due insiemi A e B non hanno elementi in comune.
  
  L'insieme vuoto è un sottoinsieme improprio di tutti gli insiemi. Quindi, è un sottoinsieme improprio sia di A che di B $$ A \cap B ⊂ A $$ $$ A \cap B ⊂ B $$

  B] Quando gli insiemi sono insiemi uguali. In questo caso l'intersezione è un insieme uguale sia ad A che a B
  

  Esempio. Dati due insiemi $$ A = \{ 1,2,3,4 \} $$ $$ B = \{ 1,2,3,4 \} $$ La loro intersezione è un insieme uguale sia ad A che a B $$ A \cap B = A = B $$ In questo caso i due insiemi A e B hanno tutti gli elementi in comune. Sono due insiemi uguali.
  
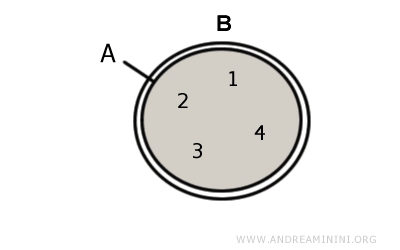
  Quando due insiemi sono uguali, sono sottoinsiemi impropri l'uno dell'altro

Le proprietà dell'intersezione

L'intersezione tra due insiemi rispetta delle proprietà simili a quelle dell'addizione e della moltiplicazione dei numeri.

• La proprietà commutativa
  Scambiando l'ordine degli insiemi l'intersezione non cambia $$ A \cap B = B \cap A $$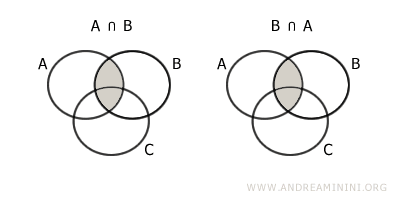

  

• La proprietà associativa
  L'intersezione di A⋂B con C è uguale all'intersezione tra A con B⋂C. $$ (A \cap B) \cap C = A \cap (B \cap C) $$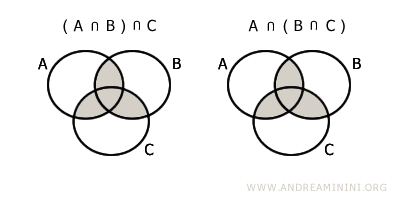

  

• La proprietà distributiva rispetto all'unione
  L'intersezione di A con B∪C è uguale all'unione delle intersezioni A⋂B e A⋂C
  $$ A \cap (B \cup C) = (A \cap B) \cup (A \cap C) $$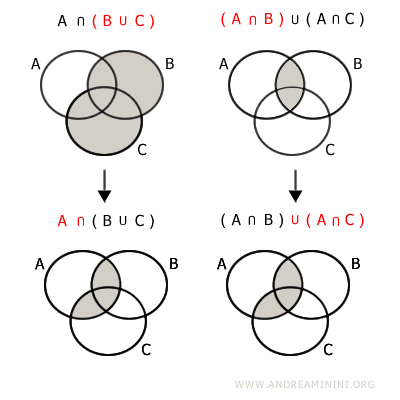

  

E così via.