Esercizio calcolo integrale 41
Devo risolvere l'integrale
$$ \int \frac{2x+5}{(x+1) \cdot (x+3)^2 } \ dx $$
La funzione integranda è il rapporto tra due polinomi e il polinomio al denominatore ha grado più alto rispetto al numeratore. Quindi, i polinomi non si possono ulteriormente dividere.
Per risolvere questo integrale utilizzo la tecnica della scomposizione in fratti semplici.
Le radici al denominatore sono x=-1 e x=-3, la prima radice (x=1) ha molteplicità uno mentre la seconda radice (x=-3) ha molteplicità due.
Pertanto, per la seconda radice considero due fratti semplici, uno con denominatore (x+3) e l'altro con denominatore (x+3)2
$$ \int \frac{2x+5}{(x+1) \cdot (x+3)^2 } \ dx = \int \frac{A}{x+1} + \frac{B}{x+3} + \frac{C}{(x+3)^2} \ dx $$
$$ \int \frac{2x+5}{(x+1) \cdot (x+3)^2 } \ dx = \int \frac{A}{x+1} + \frac{B}{x+3} + \frac{C}{(x+3)^2} \ dx $$
$$ \int \frac{2x+5}{(x+1) \cdot (x+3)^2 } \ dx = \int \frac{A \cdot (x+3)^2 + B \cdot (x+1) \cdot (x+3) + C \cdot (x+1) }{(x+1) \cdot (x+3)^2} \ dx $$
$$ \int \frac{2x+5}{(x+1) \cdot (x+3)^2 } \ dx = \int \frac{A \cdot (x^2+6x+9) + B \cdot (x^2+3x+x+3) + Cx+C}{(x+1) \cdot (x+3)^2} \ dx $$
$$ \int \frac{2x+5}{(x+1) \cdot (x+3)^2 } \ dx = \int \frac{Ax^2+6Ax+9A + Bx^2+3Bx+Bx+3B + Cx+C}{(x+1) \cdot (x+3)^2} \ dx $$
$$ \int \frac{2x+5}{(x+1) \cdot (x+3)^2 } \ dx = \int \frac{Ax^2+6Ax+9A + Bx^2+4Bx+3B + Cx+C}{(x+1) \cdot (x+3)^2} \ dx $$
$$ \int \frac{2x+5}{(x+1) \cdot (x+3)^2 } \ dx = \int \frac{x^2(A+B )+x(6A+4B+C) +9A + 3B +C}{(x+1) \cdot (x+3)^2} \ dx $$
I due membri al denominatore sono uguali.
Quindi, deduco per confronto dei numeratori che A+B=0 , 6A+4B+C=2 e 9A+3B+C=5.
Spiegazione. Il coefficiente di x2 è zero nel membro di sinistra e (A+B) nel membro di destra. Quindi A+B=0. Il coefficiente di x1=x è 2 a sinistra e (6A+4B+C) a destra. Quindi 6A+4B+C=2. Il coefficiente di x0=1 è 5 a sinistra e 9A+3B+C a destra. Quindi 9A+3B+C=5.
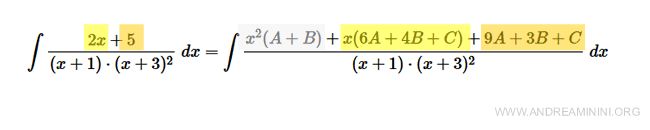
Metto le equazioni in un sistema per trovare i valori delle costanti A,B,C
$$ \begin{cases} A+B=0 \\ 6A+4B+C=2 \\ 9A+3B+C=5 \end{cases} $$
$$ \begin{cases} A=-B \\ 6(-B)+4B+C=2 \\ 9(-B)+3B+C=5 \end{cases} $$
$$ \begin{cases} A=-B \\ -2B+C=2 \\ -6B+C=5 \end{cases} $$
$$ \begin{cases} A=-B \\ C=2+2B \\ -6B+(2+2B)=5 \end{cases} $$
$$ \begin{cases} A=-B \\ C=2+2B \\ -4B=5-2 \end{cases} $$
$$ \begin{cases} A=-B \\ C=2+2B \\ B= - \frac{3}{4} \end{cases} $$
$$ \begin{cases} A=-( -\frac{3}{4} ) \\ C=2+2( -\frac{3}{4} ) \\ B= - \frac{3}{4} \end{cases} $$
$$ \begin{cases} A=\frac{3}{4} \\ C=2 -\frac{3}{2} \\ B= - \frac{3}{4} \end{cases} $$
$$ \begin{cases} A=\frac{3}{4} \\ C=\frac{4-3}{2} \\ B= - \frac{3}{4} \end{cases} $$
$$ \begin{cases} A=\frac{3}{4} \\ C=\frac{1}{2} \\ B= - \frac{3}{4} \end{cases} $$
Una volta trovate i valori delle costanti A=3/4, B=-3/4 e C=1/2 li sostituisco ai fratti semplici A, B, C dell'integrale
$$ \int \frac{2x+5}{(x+1) \cdot (x+3)^2 } \ dx = \int \frac{A}{x+1} + \frac{B}{x+3} + \frac{C}{(x+3)^2} \ dx $$
$$ \int \frac{2x+5}{(x+1) \cdot (x+3)^2 } \ dx = \int \frac{(\frac{3}{4})}{x+1} + \frac{(-\frac{3}{4})}{x+3} + \frac{(\frac{1}{2})}{(x+3)^2} \ dx $$
$$ \int \frac{2x+5}{(x+1) \cdot (x+3)^2 } \ dx = \int \frac{3}{4(x+1)} - \frac{(3}{4(x+3)} + \frac{1}{2(x+3)^2} \ dx $$
Per la proprietà lineare l'integrale di una somma è uguale alla somma degli integrali
$$ \int \frac{2x+5}{(x+1) \cdot (x+3)^2 } \ dx = \int \frac{3}{4(x+1)} \ dx - \int \frac{(3}{4(x+3)} \ dx + \int \frac{1}{2(x+3)^2} \ dx $$
$$ \int \frac{2x+5}{(x+1) \cdot (x+3)^2 } \ dx = \frac{3}{4} \int \frac{1}{(x+1)} \ dx - \frac{3}{4} \int \frac{(1}{(x+3)} \ dx + \frac{1}{2} \int \frac{1}{(x+3)^2} \ dx $$
Infine, risolvo singolarmente ogni integrale elementare
Il primo integrale è un logaritmo ∫1/(x+1)dx = log|x+1|+C
$$ \int \frac{2x+5}{(x+1) \cdot (x+3)^2 } \ dx = \frac{3}{4} \cdot \log |x+1| + C - \frac{3}{4} \int \frac{(1}{(x+3)} \ dx + \frac{1}{2} \int \frac{1}{(x+3)^2} \ dx $$
Anche il secondo integrale è un logaritmo ∫1/(x+3)dx = log|x+3|+C
$$ \int \frac{2x+5}{(x+1) \cdot (x+3)^2 } \ dx = \frac{3}{4} \cdot \log |x+1| - \frac{3}{4} \log | x+3| + C+ \frac{1}{2} \int \frac{1}{(x+3)^2} \ dx $$
L'ultimo integrale è una potenza ∫1/(x+3)2dx = - (x+3)-1
$$ \int \frac{2x+5}{(x+1) \cdot (x+3)^2 } \ dx = \frac{3}{4} \cdot \log |x+1| - \frac{3}{4} \log | x+3| - \frac{1}{2} (x+3)^{-1} +C $$
Nota. L'ultimo integrale è l'integrale di una potenza perché $$ D [ - (x+3)^{-1} ] = - ( - 1) (x+3)^{-1-1} \cdot D[x+3] = 1 \cdot (x+3)^{-2} \cdot 1 = (x+3)^{-2} = \frac{1}{(x+3)^2} $$ Pertanto $$ \int \frac{1}{(x+3)^2} \ dx = - (x+3)^{-1} $$
In conclusione, la soluzione dell'integrale è
$$ \int \frac{2x+5}{(x+1) \cdot (x+3)^2 } \ dx = \frac{3}{4} \cdot \log |x+1| - \frac{3}{4} \log | x+3| - \frac{1}{2} (x+3)^{-1} +C $$
E così via.
