I vettori geometrici
Cos'è un vettore geometrico?
Un vettore geometrico è un insieme di segmenti orientati equipollenti.
In matematica il vettore geometrico è un concetto astratto che evidenzia la qualità comune di una famiglia di segmenti equipollenti.
Cosa sono i segmenti orientati equipollenti
Dati due segmenti orientati AB e CD, sono segmenti equipollenti se hanno la stessa direzione, verso e lunghezza ( cd modulo o grandezza scalare ).

Nota. I segmenti AB e CD sono equipollenti perché hanno la stessa direzione, verso e lunghezza. Viceversa, il segmento EF non è equipollento con AB e CD perché, pur avendo la stessa direzione e lunghezza, ha un verso differente.
L'equipollenza tra due segmenti orientati si scrive

La traslazione di un segmento orientato AB sul piano cartesiano genera infiniti segmenti equipollenti.
L'insieme di tutti i segmenti equipollenti generati dalla traslazione del segmento AB, determina un vettore geometrico.

Posso così affermare che
Dato un verso, una direzione e un modulo, esiste uno e un solo vettore geometrico con queste caratteristiche.
In conclusione, il vettore geometrico è un concetto astratto che indica la qualità comune in una famiglia di segmenti equipollenti.
La differenza tra vettore libero e applicato
Il vettore può essere applicato o libero.
- Un vettore applicato è associato a un determinato punto di origine (O).
- Un vettore libero non è vincolato a un determinato punto di origine.
Un vettore geometrico libero è l'insieme di tutti gli infiniti vettori equipollenti al vettore AB ( rappresentante della classe ).
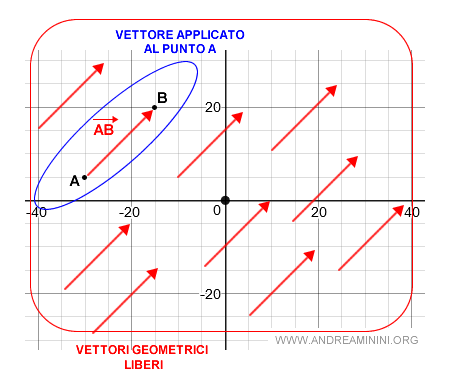
Il vettore geometrico libero è la classe di equivalenza (equipollenza) del vettore applicato AB a un punto.
Nota. Il vettore applicato di riferimento ( rappresentante di classe ) è del tutto aribitario.
L'insieme di tutti i vettori liberi del piano è detto insieme quoziente.
Come sommare i vettori geometrici
L'addizione di due vettori geometrici liberi può essere effettuata con il metodo del parallelogramma applicando i due vettori liberi a una stessa origine (O).
Un esempio pratico
Sul piano due vettori geometrici AB e CD identificano due diverse classi di equipollenza.

Per sommarli applico i due vettori allo stesso punto di origine.
Una volta scritti i due vettori AB e CD applicati a O diventano OB e OD.

Quale punto di origine scegliere? Se il piano ha un punto di origine O, conviene usare quest'ultimo perché semplifica i calcoli.
A questo punto, sommo i due vettori applicati OB+OP con il metodo del parallelogramma.

La somma dei vettori OB+OD è uguale al vettore OP

In conclusione, il vettore OP è il rappresentante della classe di equipollenza del vettore geometrico libero AB+CD.
Il vettore OP applicato a tutti gli infiniti punti del piano determina il vettore geometrico libero OP.
