Proprietà delle operazioni matematiche
Le proprietà formali delle operazioni matematiche sono le seguenti
La proprietà commutativa
Proprietà commutativa dell'addizione
In un'addizione cambiando l'ordine degli addendi, la somma non cambia. $$ a+b = b+a $$
Ad esempio
$$ 4+3 = 3+4 $$
$$ 7 = 7 $$
La proprietà commutativa non vale per la sottrazione.
Ad esempio
$$ 4-3 \ne 3-4 $$
$$ 1 \ne -1 $$
Proprietà commutativa della moltiplicazione
In una moltiplicazione cambiando l'ordine dei fattori, il prodotto non cambia.
Ad esempio
$$ 4 \cdot 3 = 3 \cdot 4 $$
$$ 12 = 12 $$
La proprietà commutativa non vale per la divisione.
Ad esempio
$$ 10 : 5 \ne 5 : 10 $$
$$ 2 \ne 0.5 $$
La proprietà associativa
Proprietà associativa dell'addizione
La somma di tre numeri a, b, c non cambia se si associano gli addendi in modo diverso lasciando invariato l'ordine degli addendi $$ (a+b)+c = a+(b+c) $$
Ad esempio
$$ (2+5)+3 = 2+(5+3) $$
$$ 7+3 = 2+8 $$
$$ 10 = 10 $$
La proprietà associativa non vale, invece, per la sottrazione
Ad esempio
$$ (2-5)-3 \ne 2-(5-3) $$
$$ -3-3 \ne 2-2 $$
$$ -3-3 \ne 2-2 $$
$$ -6 \ne 0 $$
Proprietà associativa della moltiplicazione
Il prodotto di tre numeri a, b, c non cambia se si associano i fattori in modo diverso lasciando l'ordine dei fattori invariato. $$ (a \cdot b ) \cdot c = a \cdot (b \cdot c) $$
Ad esempio
$$ (2 \cdot 5) \cdot 3 = 2 \cdot (5 \cdot 3) $$
$$ 10 \cdot 3 = 2 \cdot 15 $$
$$ 30 = 30 $$
La proprietà associativa non vale, invece, per la divisione
$$ (8 : 4) : 2 \ne 8 : (4 : 2) $$
$$ 2 : 2 \ne 8 : 2 $$
$$ 1 \ne 4 $$
La proprietà distributiva
Proprietà distributiva della moltiplicazione rispetto all'addizione
Il prodotto di un fattore a per una somma (b+c) è uguale alla somma dei prodotti ab+ac $$ a \cdot (b+c) = a \cdot b + a \cdot c $$
Ad esempio
$$ 2 \cdot (3+4) = 2 \cdot 3 + 2 \cdot 4 $$
$$ 2 \cdot 7 = 6 + 8 $$
$$ 14 = 14 $$
La proprietà distributiva della moltiplicazione rispetto all'addizione vale sia a sinistra che a destra perché la moltiplicazione gode della proprietà commutativa.
$$ (3+4) \cdot 2 = 3 \cdot 2 + 4 \cdot 2 $$
$$ 7 \cdot 2 = 6 + 8 $$
$$ 14 = 14 $$
La proprietà distributiva della moltiplicazione vale anche rispetto alla sottrazione.
$$ (4-3) \cdot 2 = 4 \cdot 2 - 3 \cdot 2 $$
$$ 1 \cdot 2 = 8 - 6 $$
$$ 2 = 2 $$
Dimostrazione geometrica
La proprietà distributiva della moltiplicazione rispetto all'addizione può essere dimostrata geometricamente.
Considero un rettangolo iniziale con la base \( a \) e l'altezza \( (b + c) \).
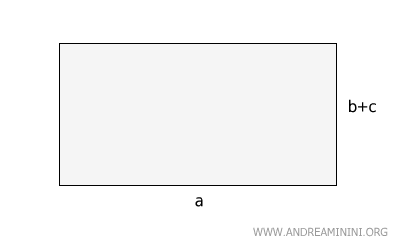
L'area $ A $ del rettangolo si ottiene moltiplicando la base per l'altezza
$$ A = a \cdot (b + c) $$
Suddivido l'altezza del rettangolo in due segmenti, \( b \) e \( c \) e ottengo due rettangoli più piccoli, ciascuno con la stessa base \( a \) ma con altezze rispettivamente \( b \) e \( c \).
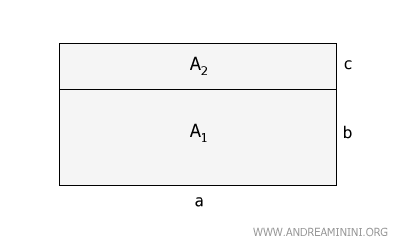
La somma delle aree di questi due rettangoli più piccoli $ A_1+ A_2 $ è uguale all'area complessiva $ A $.
$$ A = A_1 + A_2 $$
Sapendo che $ A = a \cdot (b+c) $, $ A_1 = a \cdot b $ e $ A_2 = a \cdot c $
$$ a \cdot (b + c) =a \cdot b + a \cdot c $$
In questo modo ho dimostrato la proprietà distributiva della moltiplicazione rispetto all'addizione attraverso una scomposizione geometrica con i numeri naturali.
In altre parole, l'area totale del rettangolo può essere vista sia come un unico rettangolo di altezza \( b + c \), sia come la somma delle aree di due rettangoli distinti.
Nota. La proprietà distributiva non è invece applicabile nel caso inverso dell'addizione rispetto alla moltiplicazione. $$ 2 + (3 \cdot 4) \ne ( 2 + 3 ) \cdot (2 + 4) $$ $$ 2 + 12 \ne 5 \cdot 6 $$ $$ 14 \ne 35 $$
Proprietà distributiva della divisione rispetto all'addizione
La divisione di una somma (a+b) per un divisore c<>0 diverso da zero è uguale alla somma dei quozienti tra gli addendi e il divisore $$ (a+b):c = a:c + b:c $$
Ad esempio
$$ (4+8):2 = 4:2 + 8:2 $$
$$ 12:2 = 2 + 4 $$
$$ 6 = 6 $$
Nota. La proprietà distributiva della divisione vale sia rispetto all'addizione che alla sottrazione. $$ (4-8):2 = 4:2 - 8:2 $$ $$ -4:2 = 2 - 4 $$ $$ -2 = - 2 $$
La proprietà distributiva della divisione rispetto all'addizione vale solo a sinistra perché la divisione non è un'operazione commutativa.
$$ 10:(2+5) \ne 10:2 + 10:5 $$
$$ 10:7 \ne 5 + 2 $$
$$ 10:7 \ne 7 $$
E così via.
