Frazioni algebriche

Cos'è una frazione algebrica

Una frazione algebrica è il rapporto tra due polinomi A e B $$ \frac{A}{B} $$ dove B è un polinomio non nullo.

Ad esempio, il rapporto tra i polinomi x+1 e x-1 è una frazione algebrica

$$ \frac{x+1}{x-1} $$

L'insieme delle frazioni algebriche è molto più grande dell'insieme dei polinomi perché

• Ogni polinomio è una frazione algebrica

  Nota. Posso considerare ogni polinomio come il rapporto tra il polinomio stesso e il monomio 1. Ad esempio, il polinomio x+1 è una frazione algebrica tra x+1 e 1. $$ P = x+1 = \frac{x+1}{1} $$

• La divisione tra due polinomi è sempre una frazione algebrica ma non è detto che sia anche un polinomio.

  Nota. Il risultato della divisione tra due polinomi è un polinomio solo se il resto è nullo (R=0), ossia solo nel caso in cui il polinomio al numeratore sia divisibile per il polinomio al denominatore. Ad esempio, questa frazione algebrica non è un polinomio $$ \frac{x+1}{x-1} $$ perché svolgo la divisione tra i due polinomi (x+1):(x-1) ottengo un risultato con resto non nullo (R=2).
  

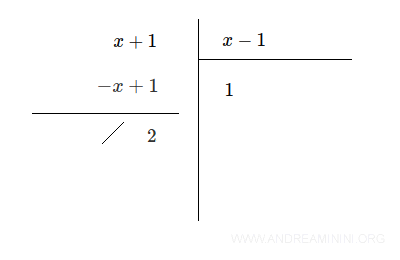
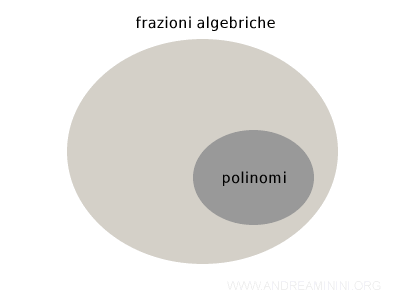
Posso affermare che tutti i polinomi sono frazioni algebriche ma non tutte le frazioni algebriche sono anche polinomi.

Pertanto, l'insieme dei polinomi è un sottoinsieme dell'insieme delle frazioni algebriche.

La condizione di esistenza

Una frazione algebrica è definita per tutti i valori delle variabili che non annullano il denominatore, perché la divisione per zero è un'operazione impossibile in matematica.

Questa condizione è detta condizione di esistenza e si indica con la sigla C.E.

Esempio. Questa frazione algebrica $$ \frac{x+1}{x-1} $$ è definita per tutti i valori della variabile x, tranne che per x=1 perché questo valore annulla il denominatore. Quindi la condizione di esistenza è la seguente $$ \text{C.E.} \ x \ne 1 $$

Un esempio pratico

Considero la frazione algebrica

$$ \frac{x+1}{x \cdot (x-1)} $$

Questa frazione è definita per qualsiasi valore della x tranne che in x=0 e x=1.

Se x=0 oppure x=1 il denominatore è uguale a zero per la legge di annullamento del prodotto-

Pertanto, la condizione di esistenza della frazione algebrica è la seguente

$$ \text{C.E.} \ x \ne 0 ∧ x \ne 1 $$

E così via.