Matematica e Informatica
Topologia
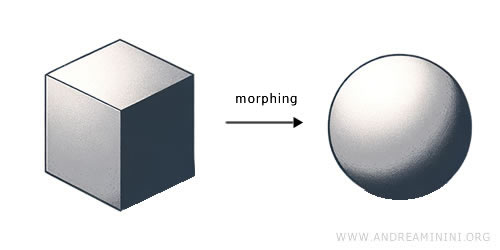La topologia è un ramo della matematica incentrato sulle proprietà dello spazio che vengono preservate sotto deformazioni continue come l’allungamento e la piegatura, ma non lo strappo o l’incollaggio. Si occupa di concetti come continuità, compattezza e connessione, ed è spesso descritta mediante la nozione di insiemi aperti. Uno spazio topologico è un insieme dotato di una topologia, ossia una raccolta di insiemi aperti che soddisfa determinati assiomi, permettendo la definizione di funzioni continue. La topologia si è sviluppata all’inizio del XX secolo, con contributi importanti di matematici come Henri Poincaré e Felix Hausdorff. Questo campo fornisce un quadro fondamentale per molte aree della matematica e della scienza, tra cui analisi, geometria e fisica quantistica.
Teoria degli Insiemi
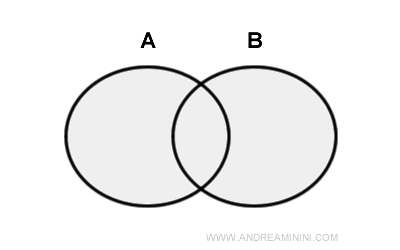
La teoria degli insiemi è un ramo fondamentale della matematica che studia gli insiemi, ovvero collezioni di oggetti ben definiti e distinti. Gli oggetti che compongono un insieme sono chiamati elementi o membri. Un insieme è considerato come un’unica entità che racchiude i suoi elementi. Gli insiemi sono solitamente indicati con lettere maiuscole (A, B, C, …), mentre i loro elementi vengono elencati tra parentesi graffe. Ad esempio, l’insieme A contenente i numeri 1, 2 e 3 si scrive: A={1,2,3}.
Matrice
Una matrice è un insieme organizzato di numeri disposti in righe e colonne, rappresentato come un array rettangolare in cui ogni numero è detto elemento della matrice. Di solito, una matrice è indicata con una lettera maiuscola, come \(A\), e i suoi elementi sono rappresentati da una lettera minuscola con due indici, come \(a_{ij}\), dove \(i\) rappresenta la riga e \(j\) la colonna. Le matrici furono introdotte nel XVII secolo dal matematico inglese James Joseph Sylvester. Tuttavia, fu Arthur Cayley nel XIX secolo a sviluppare la teoria moderna delle matrici.
Vettori
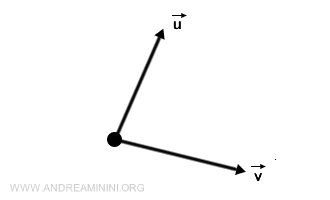Un vettore è una quantità matematica che possiede sia magnitudine sia direzione, rappresentata geometricamente da una freccia nello spazio. Nella notazione, un vettore è spesso indicato con una lettera minuscola grassetto, come \(\vec{v}\), o con una freccia sopra la lettera, come \(\vec{v}\). I vettori possono essere descritti mediante le loro componenti, che rappresentano le proiezioni sugli assi di un sistema di coordinate. Ad esempio, un vettore bidimensionale \(\vec{v}\) può essere rappresentato come \((v_x, v_y)\), dove \(v_x\) e \(v_y\) sono le componenti lungo gli assi \(x\) e \(y\), rispettivamente. Le origini della teoria dei vettori risalgono all’antichità, ma fu il matematico francese Augustin-Louis Cauchy nel XIX secolo a formalizzare il concetto e il suo impiego nelle scienze fisiche e nell’ingegneria.
Spazio Vettoriale
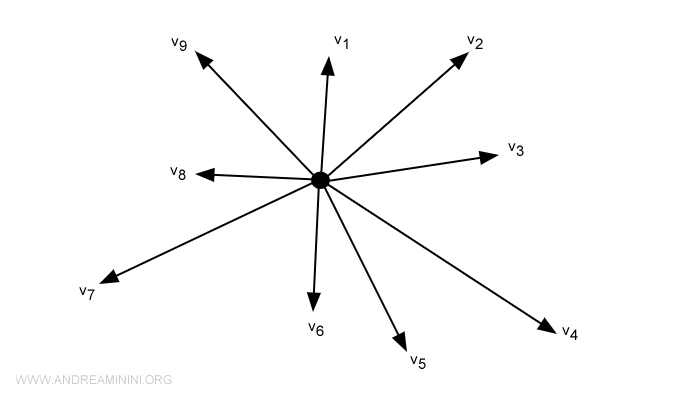Uno spazio vettoriale è una struttura matematica costituita da una collezione di vettori, che possono essere sommati tra loro e moltiplicati per scalari. Queste operazioni soddisfano determinati assiomi, come associatività, commutatività e distributività. Uno spazio vettoriale è generalmente indicato con una lettera maiuscola, come \(V\), mentre i suoi elementi, i vettori, sono rappresentati da lettere minuscole. Il concetto di spazio vettoriale è fondamentale nell’algebra lineare e fornisce un quadro per l’analisi di equazioni lineari, trasformazioni e mapping. La teoria moderna degli spazi vettoriali fu formalizzata nel XIX secolo da matematici come Hermann Grassmann e Giuseppe Peano. Questa teoria sostiene gran parte della matematica e della fisica moderne, offrendo una struttura solida per numerose applicazioni.
Algebra Astratta
L’algebra astratta è un ramo della matematica che studia le strutture algebriche come gruppi, anelli, campi e moduli. Queste strutture sono definite da insiemi dotati di operazioni che seguono specifici assiomi, quali chiusura, associatività e presenza di elementi identità. L’algebra astratta fornisce un quadro unificante per comprendere e generalizzare vari sistemi algebrici. Questo campo è indicato con lettere maiuscole, come \(A\) o \(B\), mentre gli elementi sono rappresentati con lettere minuscole. Lo sviluppo dell’algebra astratta iniziò nel XIX secolo con i lavori di matematici come Évariste Galois e Arthur Cayley, che introdussero la teoria dei gruppi per risolvere equazioni polinomiali. L’algebra astratta è essenziale in molte aree della matematica e della scienza, offrendo strumenti potenti per risolvere problemi complessi ed esplorare le strutture profonde dei sistemi matematici.
