Gruppi
Cos'è un gruppo?
- Un gruppo è una struttura algebrica (G,*) composta da
- un insieme non vuoto (G≠Ø)
- un'operazione binaria interna $$ *: G×G \rightarrow G $$ che rispetta queste tre proprietà
- soddisfa la proprietà associativa $$ (a*b)*c = a*(b*c) $$
- ammette l'esistenza di un elemento neutro (e) nell'insieme G $$ a*e=e*a=a \ \ \forall \ a \in G $$
- ammette l'esistenza di un elemento inverso per ogni elemento dell'insieme $$ a*(a)^{-1}=(a)^{-1}*a= e \ \ \forall \ a \in G $$
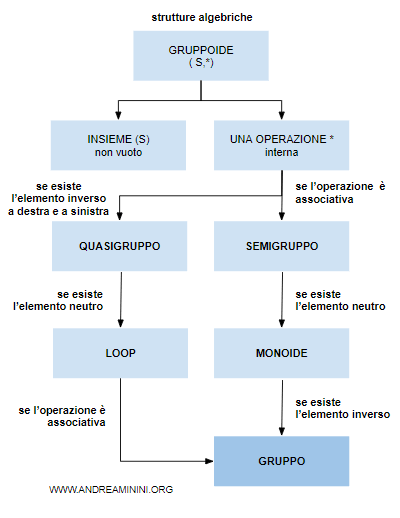
In altre parole, nell'algebra astratta un gruppo è un monoide (S,*) che include un elemento inverso nell'insieme S.
Il numero di elementi |G| dell'insieme G determina l'ordine del gruppo.
In base al numero di elementi un gruppo si dice
- gruppo finito o di ordine finito (finite order)
se il gruppo ha un numero finito di elementi. - gruppo infinito (infinite order)
se il gruppo ha infiniti elementi
I gruppi sono l'elemento fondamentale della teoria dei gruppi e dell'algebra astratta, uno dei più recenti campi di studio della matematica.
Un esempio pratico
Esempio 1
Un esempio di gruppo è l'insieme dei numeri interi (Z) rispetto all'addizione (+)
- L'addizione è un'operazione binaria (a+b) ed interna all'insieme Z. La somma di due numeri interi qualsiasi è un altro numero intero. $$ a+b = c \in Z \ \ \ \ \ \forall \ a,b \in Z $$
- L'addizione soddisfa la proprietà associativa. Presi tre interi qualsiasi a, b, c ∈ Z vale la relazione $$ (a + b) + c = a + (b + c) \ \ \ \ \ \forall \ a,b,c \in Z $$
- Nell'insieme Z esiste l'elemento neutro 0 ∈ Z. La somma tra zero e un qualsiasi numero intero è il numero intero stesso. $$ a+0=0+a=a \ \ \ \ \ \forall \ a \in Z $$
- Ogni numero intero a∈Z ha un elemento inverso (-a)∈Z rispetto all'addizione. E' l'elemento opposto. La somma tra qualsiasi numero intero e il suo opposto è sempre uguale a zero. $$ a+(-a)=(-a)+a=0 \ \ \ \ \ \forall \ a \in Z $$
In conclusione (Z, +) è un gruppo additivo.
Esempio 2
L'insieme dei numeri interi (Z) non è invece un gruppo rispetto alla moltiplicazione (·) perché non tutti gli elementi hanno l'elemento inverso della moltiplicazione.
Ad esempio, l'inverso moltiplicativo di 2 è 1/2 che non è un numero intero.
$$ 2 \cdot \frac{1}{2} = 1 $$
Nota. In questo caso l'elemento inverso della moltiplicazione è 1/2. L'insieme dei numeri interi Z rispetto alla moltiplicazione soddisfa diverse proprietà dei gruppi (operazione binaria chiusa, proprietà associativa, elemento neutro) ma non tutte. Non esiste l'elemento opposto dei numeri interi rispetto alla moltiplicazione. Pertanto, l'insieme Z non forma un gruppo con la moltiplicazione. Per vedere l'esercizio completo.
La teoria dei gruppi
La teoria dei gruppi è il ramo dell’algebra astratta che studia i gruppi.
La teoria dei gruppi nasce nel XIX secolo, quando i matematici cercavano di capire se fosse possibile risolvere tutte le equazioni algebriche con formule generali.
Grazie agli studi di Ruffini, Abel e soprattutto di Évariste Galois, si scoprì che non sempre è possibile: la risolvibilità dipende da un gruppo associato all’equazione. Questa scoperta ha segnato l'inizio della teoria dei gruppi.
Nel tempo il concetto si è evoluto: nel 1854 Arthur Cayley definì i gruppi in modo astratto, indipendentemente dalle equazioni.
In seguito, i gruppi si sono rivelati strumenti fondamentali per comprendere strutture e simmetrie in tutta la matematica e in molte applicazioni scientifiche.
Nel Novecento, grazie ai contributi di Emmy Noether, la definizione moderna di gruppo si è consolidata e la teoria si è estesa sia ai gruppi finiti che infiniti.
Oggi, la teoria dei gruppi è una delle colonne portanti della matematica moderna e dell'algebra astratta.
Gruppi Abeliani
Un gruppo è detto abeliano quando rispetta anche la proprietà commutativa.
$$ (a*b)*c = a*(b*c) $$ $$ a*n = n*a = a $$ $$ a*a' = a'*a = n $$
Esempio
L'insieme dei numeri razionali Q forma un gruppo abeliano rispetto all'operazione di somma (Q,+).
Per ogni terna di interi (a, b, c), vale la regola associativa:
$$ (a+b)+c = a+(b+c) $$
L'elemento neutro è lo zero:
$$ a + 0 = 0 + a = a $$
L'inverso di un numero è il suo opposto:
$$ a + (-a) = (-a) + a = 0 $$
Il rispetto della proprietà commutativa conferma che si tratta di un gruppo abeliano:
$$ a + b = b + a $$
Nota: Escludendo lo zero, l'insieme dei numeri razionali costituisce anche un gruppo abeliano rispetto alla moltiplicazione (Q,*), dove l'elemento neutro è 1 e l'inverso di un numero è il reciproco 1/a.
Gruppi Non Abeliani
Un gruppo è detto non abeliano se non rispetta la proprietà commutativa.
I gruppi simmetrici e diedrali sono esempi tipici di gruppi non abeliani.
Esempio
La moltiplicazione di due matrici non rispetta la proprietà commutativa.
Per questo motivo, il gruppo delle matrici rispetto alla moltiplicazione (M,*) è un gruppo non abeliano.
$$ A \cdot B \ne B \cdot A $$
Il prodotto si ottiene tramite il metodo riga per colonna.

Nota: Al contrario, il gruppo delle matrici (M,+) è abeliano rispetto all'addizione. L'ordine con cui si sommano le matrici nella somma di due matrici è irrilevante.

La Tabella di Moltiplicazione
Se un gruppo è costituito da un numero finito di elementi, non troppo elevato, esso può essere rappresentato tramite una tabella.
Ad ogni riga e colonna si assegna un elemento del gruppo finito.
| a | b | ... | z | |
|---|---|---|---|---|
| a | a*a | a*b | ... | a*z |
| b | b*a | b*b | ... | b*z |
| ... | ||||
| z | z*a | z*b | ... | z*z |
Le celle indicano il risultato dell'operazione binaria.
Esempio di Gruppo
Un gruppo S è costituito dagli elementi { 0,1,2,3,4,5,6,7 } rispetto all'operazione di addizione modulo 8.
Che cos'è l'addizione modulo 8? È un'operazione binaria della aritmetica modulare. Nell'addizione modulo 8, ogni risultato maggiore o uguale a 8 viene sostituito dal resto della divisione per 8. Ad esempio, 5+2=7, 6+2=0, 7+2=1, ecc.
La tabella di composizione del gruppo (S,+8) è la seguente:
| a+b | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 0 |
| 2 | 2 | 3 | 4 | 5 | 6 | 7 | 0 | 1 |
| 3 | 3 | 4 | 5 | 6 | 7 | 0 | 1 | 2 |
| 4 | 4 | 5 | 6 | 7 | 0 | 1 | 2 | 3 |
| 5 | 5 | 6 | 7 | 0 | 1 | 2 | 3 | 4 |
| 6 | 6 | 7 | 0 | 1 | 2 | 3 | 4 | 5 |
| 7 | 7 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
Si tratta di un gruppo perché l'operazione binaria è associativa.
$$ 1 + (2 + 3) = (1 + 2) + 3 = 6 $$
Esiste un elemento neutro (0).
$$ 1 + 0 = 1 \\ 2 + 0 = 2 \\ \vdots $$
Ogni elemento ha un inverso.
$$ 1 + 7 = 0 \\ 2 + 6 = 0 \\ 3 + 5 = 0 \\ 4 + 4 = 0 \\ 5 + 3 = 0 \\ 6 + 2 = 0 \\ 7 + 1 = 0 $$
Ordine di un Gruppo
L'ordine di un gruppo finito indica la sua dimensione, ossia il numero totale dei suoi elementi. Si rappresenta con $$ |G| $$ ed è un concetto fondamentale per comprendere la struttura del gruppo.
Esempio
Consideriamo il gruppo S { 0,1,2,3,4,5,6,7 }, con l'operazione di addizione modulo 8. In questo caso, l'ordine del gruppo è 8, poiché contiene otto elementi distinti.
$$ |S| = 8 $$
Ciò significa che il gruppo S è formato da otto elementi unici.
Ordine di un Elemento in un Gruppo
L'ordine (o periodo) di un elemento di un gruppo (indicato come g in G,*) è il più piccolo intero positivo h tale che applicando h volte l'operazione del gruppo a g si ottiene l'elemento neutro n: $$ g^h = n $$.
Se un tale intero h non esiste per g, si dice che g ha un periodo infinito.
Viceversa, se esiste un intero h per g, cioè ha un periodo finito n, allora il sottogruppo generato da g, <g>, è definito come:
$$ <g> = \{ e, g, g^1, g^2, ..., g^{n-1} \} $$
In tal caso, per ogni coppia di interi h e z (con h ≠ z), vale la relazione: $$ g^h \equiv g^z \mod n $$
Esempio
Nel gruppo S { 0,1,2,3,4,5,6,7 } con l'operazione di addizione modulo 8, l'ordine degli elementi è il seguente:
| Classe | Ordine | Esempio |
|---|---|---|
| Classe 0 | 1 | 01=0 |
| Classe 1 | 8 | 18=0 |
| Classe 2 | 4 | 24=2+2+2+2=0 |
| Classe 3 | 8 | 38=3+3+3+3+3+3+3+3=0 |
| Classe 4 | 2 | 42=4+4=0 |
| Classe 5 | 8 | 58=5+5+5+5+5+5+5+5=0 |
| Classe 6 | 4 | 64=6+6+6+6=0 |
| Classe 7 | 8 | 78=7+7+7+7+7+7+7+7=0 |
L'ordine di un elemento g è uguale alla cardinalità del sottogruppo <g> generato dall'elemento.
Esempio. La classe 2 ha ordine 4. Il sottogruppo <2> generato da 2 è: $$ <2> = \{ 2, 4, 6, 0 \} $$ Il sottogruppo <2> ha 4 elementi. Quindi la cardinalità del sottogruppo generato da 2 coincide con l'ordine di 2, che è 4.
Potenza di un Elemento nel Gruppo
In teoria dei gruppi, il concetto di potenza di un elemento è direttamente legato all'operazione del gruppo, e si distingue dall'uso convenzionale del termine in matematica.
La potenza n-esima di un elemento del gruppo rappresenta l'applicazione ripetuta n volte dell'operazione del gruppo su quell'elemento.
Esempio
Scrivere g4 significa:
$$ g^4 = g * g * g * g $$
Nota: Il risultato dipende dall'operazione del gruppo. Se l'operazione è l'addizione (+), allora g4 = g + g + g + g. Se è la moltiplicazione (*), allora g4 = g * g * g * g.
Le potenze negative, ad esempio g-4, indicano:
$$ g^{-4} = g^{-1} * g^{-1} * g^{-1} * g^{-1} $$
Per definizione, la potenza zero restituisce l'elemento neutro del gruppo:
$$ g^0 = e $$
Nota: Nei gruppi con addizione (G,+), g0 = 0; nei gruppi con moltiplicazione (G,*), g0 = 1.
Gruppi Ciclici
Un gruppo si dice ciclico se esiste un elemento g tale che tutti gli elementi di G possono essere generati applicando ripetutamente l'operazione del gruppo a g.
In altre parole, il sottogruppo generato da g coincide con l'intero insieme.
Consideriamo, ad esempio, l'aritmetica modulare in base 8 con l'addizione:
$$ G = (\{0,1,2,3,4,5,6,7\}, +) $$
Questo è un gruppo ciclico perché l'elemento 1 è un generatore, cioè tramite somme successive si ottiene l'intero insieme G.
$$ <1> = \{1, 2, 3, 4, 5, 6, 7, 0\} = G $$
Questo dimostra che G è un gruppo ciclico di ordine 8.
Caratteristiche dei Gruppi Ciclici
I gruppi ciclici sono sempre abeliani e ogni loro sottogruppo è a sua volta ciclico.
Un'importante proprietà è che l'ordine di ogni sottogruppo divide l'ordine del gruppo e, per ogni divisore dell'ordine del gruppo, esiste esattamente un sottogruppo di quell'ordine.
Sottogruppi Ciclici Infiniti
Un sottogruppo ciclico si dice infinito se l'elemento generatore ha ordine infinito, cioè produce elementi sempre diversi per ogni potenza, indipendentemente dagli interi scelti.
