I loop
Un loop è un quasigruppo (S,*) in cui esiste un elemento neutro dell'operazione tale che $$ a*x=a $$ $$ x*a=a $$
Essendo un quasigruppo, nella struttura algebrica (S,*) deve esistere un inverso destro e sinistro per ciascuna coppia di elementi a,b tale che
$$ a*d_x=b $$ $$ s_x*a=b $$
Nel caso dei loop però c'è anche l'elemento neutro (e)
In un loop per ciascuna coppia di elementi a,b esiste un unico elemento x∈S come inverso destro e sinistro tale che
$$ a*x=b $$ $$ x*a=b $$
I loop sono una categoria di gruppoidi.
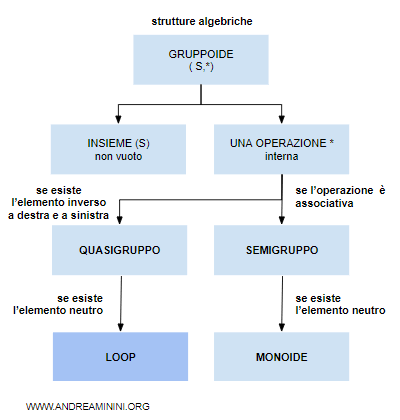
Se l'operazione * del loop soddisfa anche la proprietà associativa, la struttura algebrica è detta loop associativo o gruppo.
Un esempio pratico
L'insieme dei numeri razionali senza lo zero Q-{0} con l'operazione della moltiplicazione (·) è un loop (Q-{0},·).
$$ (Q-\{ 0 \},-) $$
Verifico le varie proprietà della struttura algebrica.
La moltiplicazione è un'operazione chiusa nell'insieme dei numeri razionali Q-{0}
$$ \forall a,b \in Q- \{ 0 \} \Longrightarrow a \cdot b \in Q- \{ 0 \} $$
Quindi, la struttura (Q-{0},·) è un gruppoide.
Esempio. Considero i numeri interi a=4 e b=7, il loro prodotto è un altro numero razionale $$ a \cdot b=4 \cdot 7=21 $$
Per qualsiasi coppia di numeri interi a,b esiste un elemento inverso sia a destra che a sinistra.
Quindi, la struttura (Z,-) è un quasigruppo.
Esempio. Considero i numeri interi a=4 e b=7. Esiste l'elemento inverso x=7/4 $$ a \cdot x = b $$ $$ 4 \cdot x = 7 $$ $$ x = \frac{7}{4} $$ e l'elemento inverso y=7/4 $$ y \cdot a=b $$ $$ y \cdot 4=7 $$ $$ y= \frac{7}{4} $$ Da notare che l'elemento inverso destro e sinistra coincide.
Nella struttura algebrica (Q-{0},·) esiste un elemento neutro dell'operazione, è il numero e=1.
$$ \forall a \in Q- \{ 0 \} \Longrightarrow a \cdot 1 = 1 \cdot a = a $$
Quindi, la struttura (Q-{0},·) è un loop.
Nota. La moltiplicazione è anche un'operazione associativa. Pertanto, la struttura algebrica (Q-{0},·) è un loop associativo ossia un gruppo. Ne consegue che tutti i gruppi sono anche loop ma non vale l'inveorso.
E così via.
