Campo in matematica

Un campo ( field ) è un insieme non vuoto K dotato di due operazioni binarie interne ( somma e prodotto ) indicate con + e · $$ (\ K \ , \ + \ , \ \cdot \ ) $$ che soddisfano le seguenti proprietà

1. Proprietà commutativa $$ x+y=y+x $$ $$ x·y=y·x $$
2. Proprietà associativa $$ (x+y)+z = x+(y+z) $$ $$ (x·y)·z = x·(y·z) $$
3. Proprietà distributiva del prodotto sulla somma $$ (x+y)·z = (x·z)+(y·z) $$ $$ x·(y+z) = (x·y)+(x·z) $$
4. Elemento neutro dell'addizione
   Esiste almeno un elemento neutro dell'addizione tale che per ogni elemento x dell'insieme K si abbia $$ 0+x = x+0 = x \ \ \ \ \forall x \in K $$
5. Elemento neutro del prodotto
   Esiste almeno un elemento neutro del prodotto tale che per ogni elemento x dell'insieme K si abbia $$ 1·x = x·1 = x \ \ \ \ \forall x \in K $$
6. Elemento inverso dell'addizione (elemento opposto)
   Per ogni elemento x dell'insieme K esiste un elemento opposto -x tale che la somma è l'elemento neutro dell'addizione $$ x+(-x) = 0 \ \ \ \ \forall x \in K $$
7. Elemento inverso del prodotto
   Per ogni elemento x≠0 diverso da zero dell'insieme K esiste un elemento inverso x^-1 tale che il prodotto è l'elemento neutro del prodotto $$ x \cdot x^{-1} = x^{-1} \cdot x = 1 \ \ \ \ \forall x \in K $$

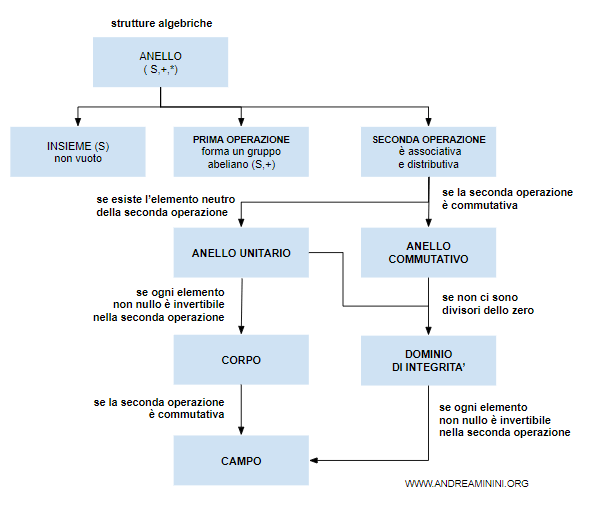
Nota. In altre parole, un campo è un anello (S,+,*) in cui anche la seconda operazione * (moltiplicazione) è commutativa, esiste l'elemento neutro dell'operazione * e l'elemento inverso dell'operazione * per ogni elemento non nullo dell'insieme S.

Un campo in cui gli elementi sono numeri è detto campo numerico (o campo di numeri).

Il campo numerico è una sottoclasse del campo generale che, invece, è definito su qualsiasi tipo di elementi (es. numeri, polinomi, funzioni e altre entità algebriche).

Un esempio pratico

Considero l'insieme dei numeri razionali Q con le operazioni di addizione (+) e moltiplicazione (·)

$$ (Q, + , \cdot ) $$

Per capire se la struttura algebrica è un campo, verifico se la prima e la seconda operazione soddisfano le relative proprietà.

La prima operazione (+)

Verifico se la prima operazione forma un gruppo abeliano (Q,+)

• L'addizione è un'operazione interna in Q $$ \forall \ a,b \in Q \ \ \ \ a+b \in Q $$
• L'addizione soddisfa la proprietà associativa $$ \forall \ a,b,c \in Q \ \ \ (a+b)+c = a+(b+c) $$
• Esiste l'elemento neutro dell'addizione $$ \forall \ a \in Q \ \ \ a + 0 = 0+a = a $$
• Esiste l'elemento opposto dell'addizione per ogni elemento di Q $$ \forall \ a \in Q \ \ \ a + (-a) = (-a)+a = 0 $$

Pertanto l'addizione forma un gruppo (Q,+) con l'insieme dei numeri razionali.

L'addizione è anche una operazione commutativa nell'insieme dei numeri razionali, quindi il gruppo (Q,+) è un gruppo abeliano.

$$ \forall \ a,b \in Q \ \ \ a+b = b+a $$

La prima operazione (+) dell'anello soddisfa tutte le proprietà dei campi.

La seconda operazione (·)

Verifico se la seconda operazione · nell'insieme Q soddisfa le proprietà di un campo

• La moltiplicazione è un'operazione interna in Q $$ \forall \ a,b \in Q\ \ \ \ a \cdot b \in Q $$
• La moltiplicazione soddisfa la proprietà distributiva rispetto alla prima operazione sia a destra che a sinistra $$ \forall \ a,b,c \in Q \ \ \ \ a \cdot (b+c) = ab+ac $$ $$ \forall \ a,b,c \in Q \ \ \ \ (a+b) \cdot c = ac+bc $$
• La moltiplicazione soddisfa la proprietà associativa $$ \forall \ a,b,c \in Q \ \ \ (a \cdot b) \cdot c = a \cdot (b \cdot c) $$
• Esiste l'elemento neutro della moltiplicazione $$ \forall \ a \in Q \ \ \ a \cdot 1 = 1 \cdot a = a $$
• Esiste l'elemento inverso della moltiplicazione in Q-{0} per ogni elemento di Q non nullo $$ \forall \ a \in Q \ , \ a \ne 0 \ \ \ a \cdot a^{-1} = a^{-1} \cdot a = 1 $$

La moltiplicazione soddisfa anche la proprietà commutativa.

$$ \forall \ a,b \in Q\ \ \ \ a+b = b+a $$

Anche la seconda operazione (·) dell'anello soddisfa tutte le proprietà dei campi

Pertanto, l'anello (Q,+,·) è un campo.

I campi commutativi

Un campo è detto commutativo se l'ordine in cui sono eseguite le operazioni di addizione moltiplicazione non influisce sul risultato finale.

In generale molti campi sono commutativi.

Esempio

Il campo dei numeri reali è un campo commutativo perché l'ordine in cui eseguo le operazioni di somma e prodotto non modifica il risultato

Ad esempio

$$ (3 + 4) = (4 + 3) = 7 $$

$$ (2 \cdot 5) = (5 \cdot 2) = 10 $$

Osservazioni

Alcune osservazioni sui campi

• Un campo è anche detto corpo commutativo.
  Un campo è anche detto "corpo commutativo" perché è un corpo in cui la moltiplicazione è commutativa. In altre parole, oltre ad avere ogni elemento non nullo invertibile, la moltiplicazione tra due elementi qualsiasi soddisfa la proprietà commutativa: \(a \cdot b = b \cdot a\). Questa proprietà distingue un campo da un corpo generico, che può non essere commutativo. Pertanto, un campo è un caso particolare di corpo.
• Differenza tra campo e campo di numeri
  La differenza tra "campo" (o campo generale) e "campo di numeri" è sottile, ma importante in contesti matematici. Un campo numerico è una sottoclasse del campo generale in cui tutti gli elementi sono numeri. Pertanto, un campo di numeri è sempre un campo ma non tutti i campi sono campi numerici.

E così via.