Gli anelli

In questa definizione ho usato l'insieme dei numeri reali R per semplificare la spiegazione. In generale, può trattarsi di qualsiasi insieme.

La prima operazione (+) e la seconda operazione (·) devono soddisfare condizioni differenti.

In particolar modo la prima operazione di un anello deve formare un gruppo abeliano (R,+)

Nota. In un anello la somma deve essere commutativa mentre la moltiplicazione può anche non esserlo. Inoltre, in un anello deve esistere l'elemento neutro e l'elemento opposto della somma. Non è richiesto che esista anche per la moltiplicazione. Infine, l'ordine delle operazioni è importante nel definire un anello. Ad esempio, la struttura (R,+,·) è un anello mentre la struttura (R,·,+) non è un anello perché non esiste l'elemento inverso del numero zero. Detto in altri termini (R,+) è un gruppo abeliano mentre (R,·) non è un gruppo. Quindi, (R,·) non è nemmeno un gruppo abeliano.

Inoltre, per prassi la prima operazione di un anello è detta "addizione" e la seconda operazione è detta "moltiplicazione".

Non è però detto che debbano essere necessariamente l'addizione e la moltiplicazione. Potrebbero anche essere operazioni diverse.

Un esempio pratico

L'insieme delle matrici quadrate M_n(Z) di ordine n (ossia n righe e n colonne) sono un anello nel campo dei numeri Z rispetto alle operazioni binarie di addizione elemento per elemento e di moltiplicazione riga per colonna

$$ (M_n(Z),+, \cdot) $$

Entrambe le operazioni di addizione e di moltiplicazione sono chiuse, perché il risultato che ottengo è sempre una matrice quadrata.

$$ M_n(Z) \ × \ M_n(Z) \rightarrow M_n(Z) $$

Verifico se anche le altre proprietà sono soddisfatte.

La prima operazione

L'addizione elemento di elemento tra due matrici quadrate soddisfa la proprietà commutativa

$$ A + B = B + A \ \ \ \ \ \ \forall \ A, B \in M_n(Z) $$

Soddisfa anche la proprietà associativa

$$ (A + B) + C = A + (B + C) \ \ \ \ \ \ \forall \ A, B, C \in M_n(Z) $$

Esiste l'elemento neutro dell'addizione. E' la matrice nulla.

Per ogni matrice quadrata esiste anche l'elemento opposto

$$ A + (-A) \ \ \ \ \ \ \ \forall \ A \in M_n(Z) $$

Tutte le proprietà della prima operazione di un anello sono soddisfatte.

Nota. La struttura (M_n(Z),+) è un gruppo perché l'insieme non è vuoto, è un'operazione chiusa, soddisfa la proprietà associativa, esiste l'elemento neutro e l'elemento inverso di ogni elemento. Inoltre, poiché soddisfa anche la proprietà commutativa, (M_n(Z),+) è un gruppo abeliano.

La seconda operazione

La prima operazione è la moltiplicazione riga per colonna di due matrici quadrate.

Soddisfa la proprietà associativa

$$ (A \cdot B) \cdot C = A \cdot (B \cdot C) \ \ \ \ \ \ \forall \ A, B, C \in M_n(Z) $$

Soddisfa la proprietà distributiva

$$ (A + B) \cdot C = A \cdot C + B \cdot C \ \ \ \ \ \ \forall \ A, B, C \in M_n(Z) $$

$$ A \cdot ( B + C ) = A \cdot B + A \cdot C \ \ \ \ \ \ \forall \ A, B, C \in M_n(Z) $$

La seconda operazione soddisfa tutte le proprietà di un anello.

Conclusione

In conclusione, la prima e la seconda operazione soddisfano tutte le proprietà degli anelli.

Pertanto, la struttura algebrica (M_n(Z),+,*) è un anello.

Tipi di anelli

Gli anelli possono soddisfare anche proprietà aggiuntive ma non obbligatorie

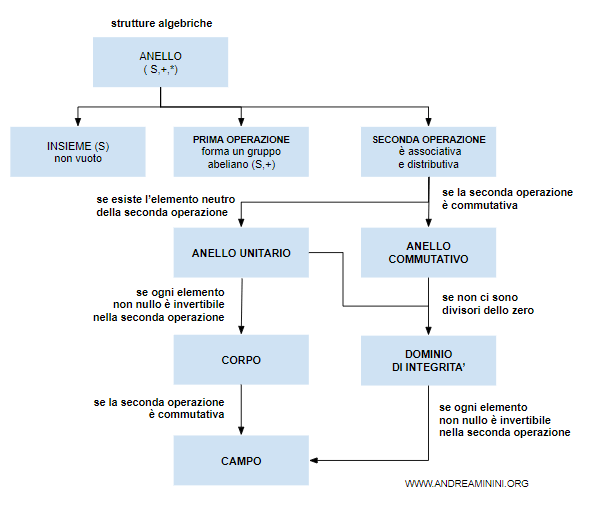
In questi casi si parla di

• Anello commutativo
  Si parla di anello commutativo (R,+,·) se anche la moltiplicazione soddisfa la proprietà commutativa $$ a \cdot b = b \cdot a \ \ \ \forall \ a,b \in R $$
• Anello unitario o con unità
  Si parla di anello unitario (R,+,·) se esiste l'elemento neutro anche della moltiplicazione. $$ a \cdot 1 = 1 \cdot a = a \ \ \ \forall \ a \in R $$
• Dominio di integrità
  Si parla di dominio di integrità se l'anello è commutativo e unitario e non esistono dei divisori dello zero $$ \forall \ a,b \in R \ \ \ \ ab \Rightarrow a=0 \ ∨ \ b= 0 $$
• Corpo
  Un corpo (R,+,·) è un anello è unitario ed esiste anche l'elemento inverso della moltiplicazione per ogni elemento non nullo dell'insieme R. $$ a \cdot a^{-1} = 1 \ \ \ \forall \ a \ , \ a \ne 0 \ \in R $$
• Campo
  Si parla di campo (R,+,·) se l'anello è commutativo, unitario ed esiste anche l'elemento inverso della moltiplicazione per ogni elemento non nullo dell'insieme R. $$ a \cdot a^{-1} = 1 \ \ \ \forall \ a \ , a \ne 0 \ \in R $$

E così via.