I domini di integrità
Un dominio di integrità è un anello commutativo e unitario (S,+,·) privo di divisori dello zero. $$ \forall \ a, b \in S \ , \ ab=0 \Rightarrow ( a=0 \ ∨ \ b= 0 ) $$
In altre parole, un dominio di integrità è un anello commutativo in cui, se ab=0, allora a=0 oppure b=0.
Per capire se un anello commutativo (S,+,·) è un dominio di integrità, devo dimostrare che non ci siano divisori dello zero nell'insieme S.
Cos'è un divisore dello zero? In un anello commutativo (S,+,·) un elemento non nullo a≠0 dell'insieme S è detto divisore dello zero se esiste un altro elemento non nullo b≠0 dell'insieme S tale che ab=0
Un esempio pratico
L'insieme dei numeri interi Z forma un anello (Z,+,·) rispetto all'addizione e alla moltiplicazione
$$ (Z,+,·) $$
Si tratta di un anello commutativo perché anche la moltiplicazione soddisfa la proprietà commutativa.
Il prodotto di due numeri interi non nulli a≠0 e b≠0 è sempre diverso da zero.
$$ \forall \ a,b \in Z \ , \ a \ne 0 \ , \ b \ne 0 \ \ \Longrightarrow \ \ ab \ne 0 $$
Nota. Se prendo due numeri interi con lo stesso segno (concordi) il prodotto è sempre un numero positivo. Se prendo due numeri interi con segno diverso (discordi) il prodotto è sempre negativo. Quindi, se il prodotto di due numeri interi è nullo $$ ab = 0 $$ almeno uno dei due fattori deve essere uguale a zero. $$ a \cdot 0 = 0 \cdot a = 0 $$
Pertanto, nell'insieme Z non ci sono divisori dello zero.
Ne consegue che l'anello commutativo (Z,+,·) è un dominio di integrità.
Esempio 2
Considero l'insieme delle classi resto modulo 6
$$ Z_6 = \{ 0,1,2,3,4,5 \} $$
L'insieme Z6 forma un anello commutativo (Z6,+,·) rispetto all'addizione (+) e alla moltiplicazione (·)
$$ (Z_6,+, \cdot) $$
Costruisco la tavola moltiplicativa dell'anello per verificare se ci sono dei divisori dello zero
| a ·6 b | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 | 5 |
| 2 | 0 | 2 | 4 | 0 | 2 | 4 |
| 3 | 0 | 3 | 0 | 3 | 0 | 3 |
| 4 | 0 | 4 | 2 |
0 | 4 | 2 |
| 5 | 0 | 5 | 4 | 3 | 2 | 1 |
In questo caso ci sono tre divisori dello zero. Sono i numeri 2, 3 e 4
Ad esempio, il prodotto 2·3 è uguale a zero perché ha resto nullo
$$ 2 \cdot 3 ≡ 0 \ mod \ 6 $$
Spiegazione. Calcolo il prodotto tra i numeri 2 e 3 $$ 2 \cdot 3=6 $$ Poi calcolo il resto della divisione del prodotto appena ottenuto (2·3=6) per il modulo 6 della classe $$ 6:6=1 \ \ r =0 $$ Il resto della divisione è zero. Quindi, nella classe modulo 6 l'operazione 2·3=0. Lo stesso risultato ottengo nel prodotto 3·2=0
Pertanto, essendoci dei divisori dello zero, l'anello commutativo (Z6,+,·) non è un dominio di integrità.
In generale, un gruppo commutativo Zn è un dominio di integrità solo se il numero di elementi (n) è un numero primo.
Esempio 3
Considero l'insieme delle classi resto modulo 7
$$ Z_7 = \{ 0,1,2,3,4,5,6 \} $$
In questo caso il numero di elementi è un numero primo (n=7)
L'insieme Z7 forma un anello commutativo (Z7,+,·) rispetto all'addizione (+) e alla moltiplicazione (·)
$$ (Z_7,+, \cdot) $$
Costruisco la tavola moltiplicativa dell'anello per verificare se esistono dei divisori dello zero
| a ·7 b | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 2 | 0 | 2 | 4 | 6 | 1 | 3 | 5 |
| 3 | 0 | 3 | 6 | 2 | 5 | 1 | 4 |
| 4 | 0 | 4 | 1 |
5 | 2 | 6 | 3 |
| 5 | 0 | 5 | 3 | 1 | 6 | 4 | 2 |
| 6 | 0 | 6 | 5 | 4 | 3 | 2 | 1 |
In questo caso ci sono non ci sono divisori dello zero.
Pertanto, l'anello commutativo (Z7,+,·) è un dominio di integrità.
Osservazioni
Alcune osservazioni e note sui domini di integrità
-
Se esiste l'elemento inverso della moltiplicazione (seconda operazione) per ogni elemento non nullo, allora il dominio di integrità è un campo.
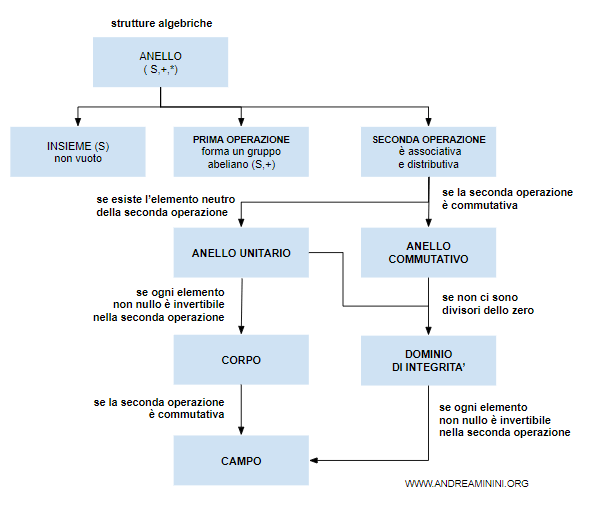
- Un dominio di integrità finito è anche un campo
Un dominio di integrità è un campo se tutti gli elementi sono invertibili nella moltiplicazione (seconda operazione).Dimostrazione. Considero un dominio di integrità (D,+,·) con un numero finito di n elementi diversi tra loro $$ D=\{ a_1,a_2, ..., a_n \} $$ Sottolineo che tutti gli elementi sono diversi tra loro.
Esempio. Per verificare i passaggi con valori numerici considero l'insieme finito Z7 $$ D=\{0,1,2,3,4,5,6 \} $$ e il dominio di integrità (Z7,+,·).
Prendo un elemento qualsiasi ak di D diverso da zero (ak≠0). $$ a_k \ne 0 $$ Costruisco un applicazione che moltiplica l'elemento ak per gli altri elementi $$ f: a_k \cdot a_i $$ Ottengo dei prodotti diversi tra loro. Quindi, l'applicazione f è iniettiva Poiché l'insieme D è anche finito, l'applicazione f è anche suriettiva.
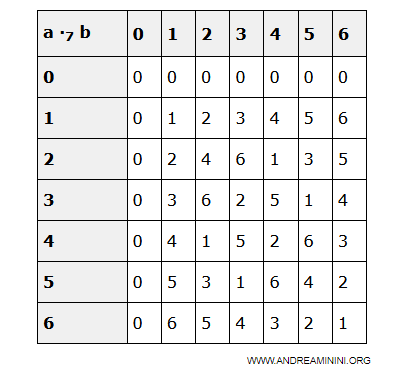
Esempio. Se scelgo ak=5 in Z7, i prodotti con gli altri elementi di Z7 sono tutti diversi.
Questo vuol dire che a sua volta ak è sicuramente uguale al prodotto per qualche altro elemento a0 di D $$ a_k = a_k \cdot a_0 = a_0 \cdot a_k $$
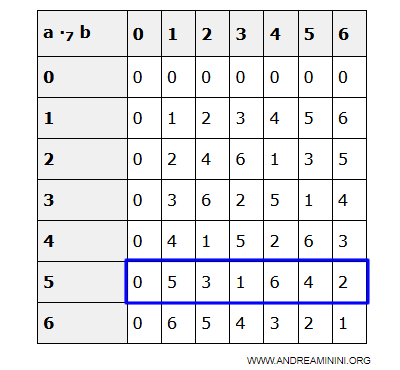
Esempio. Nell'esempio numerico se ak=5 allora a0=1 perché $$ 5 = 5 \cdot 1 = 1 \cdot 5 $$
Quindi, un qualsiasi elemento x di D è uguale al prodotto di ak per qualche ai $$ x = a_k \cdot a_i $$
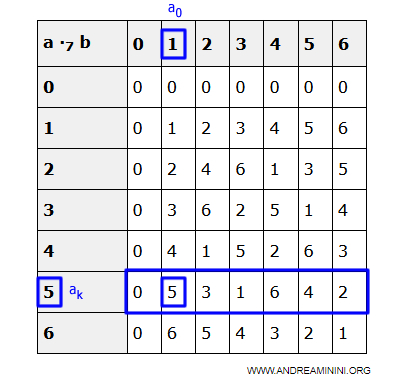
Esempio. Basta riguardare la tavola moltiplicativa del caso Z7. Il prodotto di ak=5 per gli elementi di Z7 genera tutti gli elementi di Z7. $$ 5 \cdot 0 = 0 \\ 5 \cdot 1 = 5 \\ 5 \cdot 2 = 3 \\ 5 \cdot 3 = 1 \\ 5 \cdot 4 = 6 \\ 5 \cdot 5 = 4 \\ 5 \cdot 6 = 2 $$
Sapendo che ak=ak·a0 $$ x = ( a_k \cdot a_0 ) \cdot a_i $$ Per la proprietà commutativa $$ x = ( a_0 \cdot a_k ) \cdot a_i $$ Per la proprietà associativa $$ x = a_0 \cdot (a_k \cdot a_i) $$ Sapendo che x=akai $$ x = a_0 \cdot x $$ Poiché in un dominio di integrità la moltiplicazione è commutativa $$ x = a_0 \cdot x = x \cdot a_0 $$ Quindi a0=1 è l'elemento neutro della moltiplicazione (unità) in D $$ a_0 = 1 $$ Questo dimostra l'esistenza dell'elemento neutro (unità) della moltiplicazione in D. Ne consegue che l'elemento unità 1 esiste nell'insieme D ed è uguale al prodotto di ak per qualche aj $$ 1 = a_k \cdot a_j $$Esempio. Nell'esempio numerico con Z7, considerando ak=5, l'elemento aj=3 perché $$ 1 =5 \cdot 3 $$
Questo dimostra anche che l'elemento ak è invertibile per qualche elemento aj dell'insieme D.
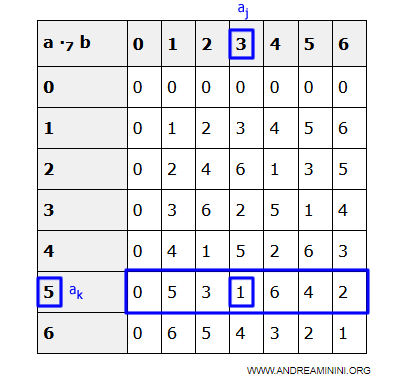
Esempio. Nell'esempio numerico di Z7 con ak=5 e aj=3 $$ 1 = 5 \cdot 3 $$ Di conseguenza, l'elemento inverso di ak=5 è ak-1= 3.
In conclusione, tutti gli elementi non nulli dell'insieme D sono invertibili.Esempio. Nell'esempio numerico di Z7 tutti gli elementi non nulli dell'insieme Z7 hanno l'elemento inverso. Ad esempio, l'elemento inverso di 1 è 1, l'elemento inverso di 2 è 4, l'elemento inverso di 3 è 5, l'elemento inverso di 4 è 2, l'elemento inverso di 5 e 3, l'elemento inverso di 6 è 6.
Di conseguenza, il dominio di integrità (D,+,·) è un campo.
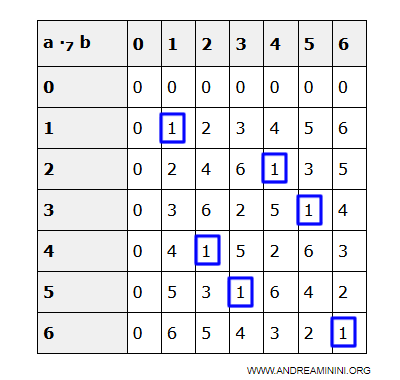
E così via
