Gruppi ciclici
Un gruppo (G,*) è detto gruppo ciclico se esiste un elemento g∈G (detto generatore) in grado di generare tutti gli elementi del gruppo G.
Nei gruppi ciclici moltiplicativi l'insieme G è uguale all'insieme delle potenze dell'elemento generatore (g)
$$ G = \{ \ g^n \ : \ n \in Z \ \} $$
Dove n è un numero intero.
Nei gruppi ciclici additivi, invece, l'insieme G è uguale all'insieme dei multipli dell'elemento generatore (g)
$$ G = \{ \ g \cdot n \ : \ n \in Z \ \} $$
Nota. In pratica, nei gruppi ciclici l'insieme G è uguale al sottogruppo <g> generato dall'elemento generatore $$ G = <g> = \{ g^1, ... , g^n \} $$ Dove il termine gn è l'elemento neutro del gruppo.
L'ordine del generatore è il minimo intero n per il quale il generatore gn è uguale all'elemento neutro (u) del gruppo.
$$ g^n = u $$
Se non esiste un numero n allora il generatore è di ordine infinito.
Un esempio pratico
Il gruppo composto dall'insieme finito di numeri interi Z4={0,1,2,3} dell'aritmetica modulare e dall'operazione di addizione + è un gruppo ciclico
$$ (Z_4, +) $$
perché esiste in Z4 un elemento generatore (g=1) in grado di generare tutti gli elementi di G
$$ g = 1 $$
In questo caso l'elemento generatore è il numero 1.
$$ 1^1 = 1 $$ $$ 1^2 = 1+1 = 2 $$ $$ 1^3 = 1+1+1 = 3 $$ $$ 1^4 = 1+1+1+1 = 0 $$
Il periodo dell'elemento 1 è uguale 4 perché sono necessarie 4 ripetizioni dell'operazione per tornare all'elemento neutro (e=0) del gruppo.
Nota. Nel caso dei gruppi (Z4,+) la potenza 13 va intesa come l'operazione del gruppo, in questo caso l'addizione +, ripetuta tre volte 13 =1+1+1 sull'elemento 1. Quindi, non è la potenza algebrica.
Il sottogruppo <1> generato dall'elemento 1 coincide con l'insieme G
$$ <1> = \{ 0,1,2,3 \} = G $$
La cardinalità del sottogruppo <1> è uguale a 4 perché è composta da 4 elementi.
Quindi, il sottogruppo <1> è di ordine 4.
L'elemento 2 invece non è un generatore perché i suoi multipli (potenze) non generano tutti gli altri elementi dell'insieme Z4.
$$ 2^0 = 0 $$ $$ 2^1 = 2 $$ $$ 2^2 = 2+2 = 0 $$
Il periodo dell'elemento 2 è uguale 2 perché sono necessarie due operazioni per tornare all'elemento neutro del gruppo e=0.
Il sottogruppo <2> generato dall'elemento 2 è composto solo da due elementi, quindi il sottogruppo è di ordine 2.
$$ <2> = \{ 0,2 \}$$
Nota. Il periodo dell'elemento 2 e l'ordine del sottogruppo <2> sono uguali. Il sottogruppo <2> è di ordine 2 perché è composti da due elementi (0 e 2). Il periodo di 2 è uguale 2 perché il numero intero più piccolo k tale che gk=0 la potenza del generatore g=2 sia uguale all'elemento neutro (e) è k=2 $$ 2^2 = 2 +2 = 0 $$
Anche l'elemento 3 è un generatore del gruppo ciclico
$$ 3^1 = 3 $$ $$ 3^2 = 3+3 =2 $$ $$ 3^3 = 3+3 + 3 =1 $$ $$ 3^4 = 3+3+3+3 =0 $$
perché il sottogruppo <3> generato dall'elemento 3 coincide con l'insieme G
$$ <3> = \{ 0,1,2,3 \} = G $$
Il sottogruppo <3> è di ordine 4 perché è composto da 4 elementi.
Il periodo dell'elemento 3 è uguale a 4 perché sono necessarie quattro ripetizioni dell'operazione per avere l'elemento neutro e=0 del gruppo.
Nota. Ovviamente non considero l'elemento 0 perché sicuramente non è un generatore, in quanto l'elemento 0 è l'elemento neutro del gruppo (Z4,+). $$ 0^1 = 0 $$ $$ 0^2 = 0+0 = 0 $$
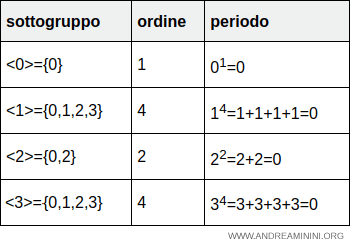
Pertanto i sottogruppi generati dagli elementi del gruppo (Z4,+) sono
| sottogruppo | ordine | periodo |
|---|---|---|
| <0>={0} | 1 | 01=0 |
| <1>={0,1,2,3} | 4 | 14=1+1+1+1=0 |
| <2>={0,2} | 2 | 22=2+2=0 |
| <3>={0,1,2,3} | 4 | 34=3+3+3+3=0 |
Di questi soltanto i sottogruppi generati dagli elementi 1 e 3 coincidono con il gruppo Z4
$$ <1>=<3>= \{ 0,1,2,3 \}=Z_4 $$
Pertanto, gli elementi 1 e 3 sono generatori del gruppo ciclico (Z4,+)
Le proprietà dei gruppi ciclici
Alcune proprietà dei gruppi ciclici
- I gruppi ciclici sono anche gruppi abeliani (gruppi commutativi)
- Se (G,*) è un gruppo ciclico allora anche i suoi sottogruppi sono gruppi ciclici
Esempio. Il gruppo (Z4,+) è un gruppo ciclico di ordine n=4 e ha i seguenti sottogruppi
Anche i suoi sottogruppi sono gruppi ciclici. Tutti includono l'elemento neutro (e=0) e tornano all'elemento neutro dopo un numero finito di ripetizioni dell'operazione (periodi). - Ogni gruppo ciclico finito di ordine n è isomorfo al gruppo Zn delle classi di resto modulo n.
- Se (G,*) è un gruppo ciclico finito di ordine n, l'elemento m∈G può essere un generatore di G se m e n sono numeri coprimi, ossia se e solo se MCD(n,m)=1.
Esempio. Il gruppo (Z4,+) è un gruppo ciclico di ordine n=4. Il gruppo ha due elementi generatori 1 e 3. Gli elementi m=1 e m=3 sono entrambi coprimi rispetto a n: MCD(1,4)=1 e MCD(3,4)=1

- Teorema di Cauchy
Se (G,*) è un gruppo ciclico finito di ordine n e p è un numero primo che divide n, allora in G esiste un elemento di ordine p - Corollario del teorema di Cauchy
Se l'ordine n di un gruppo finito (G,*) è un numero primo, allora il gruppo è ciclico. - Ogni gruppo ciclico infinito è isomorfo al gruppo (Z,+) dei numeri interi rispetto all'addizione e l'elemento 1 è il generatore del gruppo.
E così via.
