I monoidi
Un monoide è un semigruppo (S,*) con un elemento neutro e∈S. $$ \forall a \in S \rightarrow e*a=a*e=a $$
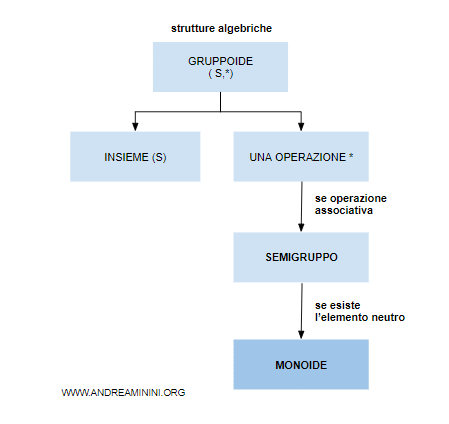
Una struttura algebrica (S,*) è un monoide se è un gruppoide che soddisfa tutte le proprietà dei semigruppi (associatività) e ha un elemento neutro (e) dell'operazione * all'interno dell'insieme S.
Esempio
Il semigruppo (N,·) è composto dall'insieme dei numeri naturali e dall'operazione di moltiplicazione (·).
Questo gruppoide è un semigruppo perché la moltiplicazione è associativa.
E' anche un monoide perché nel semigruppo esiste un elemento neutro.
E' il numero 1.
Il prodotto di qualsiasi numero del semigruppo (N,·) moltiplicato per 1 è il numero stesso.
$$ a \cdot 1 = 1 \cdot a = a $$
E così via.
