I gruppoidi
Cos'è un gruppoide?
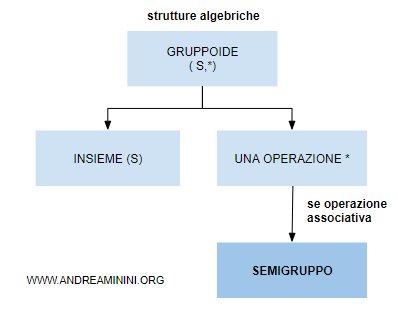
Un gruppoide (groupoid o magma) è una struttura algebrica (S,*) composta da un insieme non vuoto S e da un'operazione binaria chiusa S×S→S
In algebra astratta il gruppoide è la struttura elementare da cui derivano tutte le altre.
Le varie strutture algebriche sono gruppoidi a cui sono aggiunti altri assiomi.
Nota. Se l'operazione del gruppoide è un'addizione si parla di gruppoide additivo (S,+). Se invece l'operazione del gruppoide è una moltiplicazione si parla di gruppoide moltiplicativo (S,*).
Se l'operazione del gruppoide soddisfa anche la proprietà associativa si parla di pseudogruppo o anche semigruppo.
Se esiste l'elemento inverso si parla di quasigruppo.
Un esempio pratico
Esempio 1
La struttura (N,+) è un gruppoide.
E' composta dall'insieme dei numeri naturali N e dall'operazione di addizione (+).
Dati due elementi qualsiasi dell'insieme dei numeri naturali, la loro somma è un numero naturale
$$ a+b \ \in N \ \ \ \ \ \ \forall \ a,b \in N $$
L'operazione di addizione (+) è un'operazione chiusa nell'insieme dei numeri naturali N.
Nota. Un altro esempio di gruppoide è la struttura (N,*) perché anche la moltiplicazione è un'operazione chiusa nei numeri naturali.
Esempio 2
La struttura (N,-) non è un gruppoide perché la sottrazione non è un'operazione interna ai numeri naturali.
Ad esempio
$$ 4 - 5 = -1 \notin N $$
Nota. La sottrazione forma, invece, un gruppoide con l'insieme dei numeri interi (Z,-) perché la sottrazione è un'operazione interna ai numeri interi.
E così via.
