I quasigruppi
Un quasigruppo è un gruppoide (S,*) in cui per ciascuna coppia di elementi a,b esiste un elemento inverso destro (dx) e un inverso sinistro (sx) tale che $$ a*d_x=b $$ $$ s_x*a=b $$
I quasigruppi sono una categoria di gruppoidi.
Pertanto, un quasigruppo è sempre un gruppoide ma non è detto l'inverso.
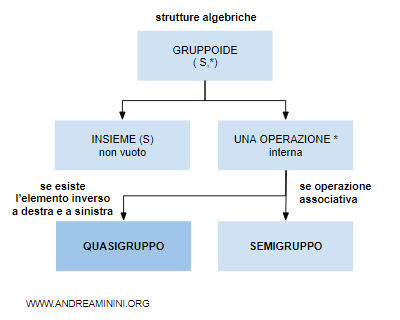
Se un quasigruppo contiene anche l'elemento neutro dell'operazione è detto loop.
Un esempio pratico
L'insieme dei numeri interi Z con l'operazione di sottrazione (-) è un quasigruppo (Z,-).
$$ (Z,-) $$
Verifico le varie proprietà della struttura algebrica.
La sottrazione è un'operazione chiusa nell'insieme dei numeri interi (Z) perché la differenza di qualsiasi coppia di numeri interi è a sua volta un numero intero.
$$ \forall a,b \in Z \Longrightarrow a-b \in Z $$
Quindi, la struttura (Z,-) è un gruppoide.
Esempio. Considero i numeri interi a=4 e b=7, la loro differenza è un altro numero intero $$ a-b=4-7=-3 $$
Per qualsiasi coppia di numeri interi a,b esiste un elemento inverso sia a destra che a sinistra.
Quindi, la struttura (Z,-) è un quasigruppo.
Esempio. Considero i numeri interi a=4 e b=7. Esiste l'elemento inverso x=-3 $$ a-x = b $$ $$ 4-x = 7 $$ $$ x = 4-7 $$ $$ x=-3 $$ e l'elemento inverso y=11 $$ y-a=b $$ $$ y-4=7 $$ $$ y-4=7 $$ $$ y=7+4 $$ $$ y=11 $$
E così via.
