Il tronco di piramide
Il tronco di piramide è una figura geometrica solida che si ottiene sezionando una piramide con un piano parallelo alla sua base. La sezione crea una nuova faccia, più piccola rispetto alla base originale, e trasforma la piramide in un solido a due basi.
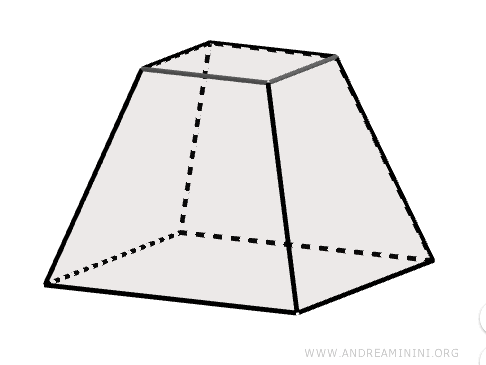
L'intersezione tra una piramide e un piano parallelo alla sua base genera due solidi distinti:
- Una piramide più piccola, situata nella parte superiore, con vertice \( V \) e base \( A'B'C'D' \). Questa piramide mantiene lo stesso vertice della piramide originaria \( ABCDV \) e le due figure sono in rapporto di similitudine.
- Un tronco di piramide, situato nella parte inferiore, delimitato da due basi poligonali parallele e da facce laterali di forma trapezoidale.
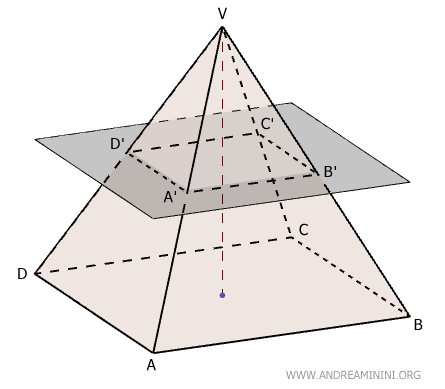
In un tronco di piramide le basi sono parallele e simili tra loro, ma di dimensioni diverse.
La base maggiore (ABCD) è quella originale della piramide, mentre la base minore (A'B'C'D') è quella creata dalla sezione del piano con la piramide.
Le facce laterali del tronco di piramide sono trapezi. Nel caso particolare di una piramide regolare, le facce laterali sono trapezi isosceli.
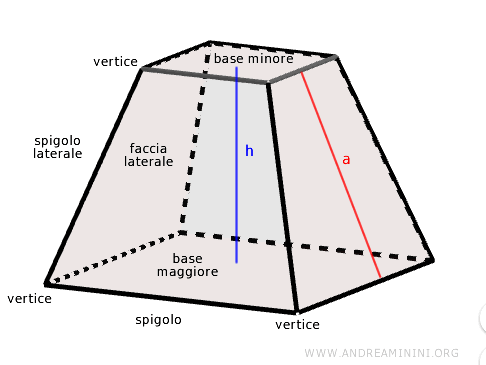
Il numero di facce laterali è uguale al numero di lati della base della piramide.
Questa regolare è valida indipendentemente dalla forma della base della piramide, che può essere un poligono regolare o irregolare.
Per il resto valgono gli stessi concetti già visti per gli altri solidi poliedri:
- L'altezza (h) è la distanza perpendicolare tra le due basi.
- I vertici del tronco di piramide sono i vertici della base maggiore e della base minore.
- Gli spigoli laterali sono i segmenti che connettono i vertici delle due basi
- L'apotema (a) è utile per calcolare la superficie laterale.
Il tronco di piramide regolare è un tronco di piramide ottenuto da una piramide regolare. Il tronco di piramide regolare è caratterizzato da trapezi isosceli nelle facce laterali, tutti congruenti tra loro. L'altezza di ogni trapezio isoscele è l'apotema del tronco di piramide. E' un tronco di piramide retto se deriva da una piramide retta, ovvero una piramide in cui il vertice è perfettamente allineato con il centro della base e l’asse della piramide è perpendicolare al piano della base.
Le formule
Le formule per calcolare la superficie e il volume del tronco di piramide.
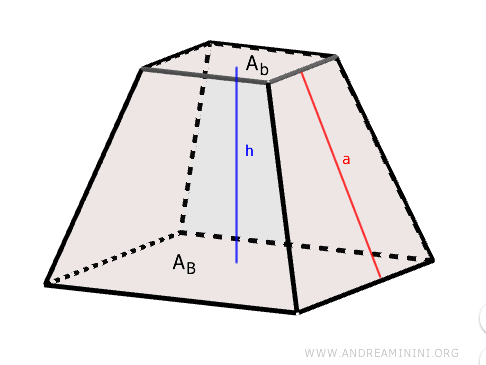
- Area Laterale (Al)
Si calcola sommando l'area di tutte le facce laterali (trapezi). In alternativa, si può calcolare moltiplicando la somma dei semiperimetri delle basi per l'apotema. $$ A_l = (p_B + p_b) \cdot a $$ Dove pB e pb sono rispettivamente il semiperimetro della base maggiore e della base minore mentre "a" è l'apotema.Dimostrazione. Considero una piramide regolare e retta su base quadrata.
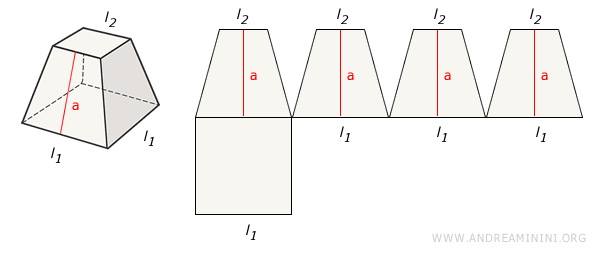
L'area laterale è la somma delle aree delle facce. In questo caso, per semplicità ogni faccia ha la stessa area, quella di un trapezio ossia $ \frac{(l_1+l_2) \cdot a}{2} $. Il discorso è comunque più generale e vale anche se avessero aree diverse. $$ A_l = 4 \cdot \frac{(l_1+l_2) \cdot a}{2} $$ $$ A_l = \frac{(4l_1+4l_2) \cdot a}{2} $$ Ora $ P_B=4l_1 $ è il perimetro della base inferiore della piramide tronca mentre $ P_b = 4l_2 $ è il perimetro della base superiore. $$ A_l = \frac{(P_B+P_b) \cdot a}{2} $$ Sapendo che $ p_B = \frac{P_B}{2} $ è il semiperimetro della base inferiore della piramide e $ p_b = \frac{P_b}{2} $ è il semiperimetro della base superiore. $$ A_l = (p_B+p_b) \cdot a $$ Concludo che l'area laterale è il prodotto tra la somma dei semiperimetri delle basi della piramide tronca e l'apotema. Come volevasi dimostrare. - Area Totale (At)
È la somma dell'area laterale e delle aree delle due basi. $$ A_t = A_B+A_b+A_l $$ - Volume (V)
Si calcola usando la formula: $$ V = \frac{1}{3}h(A_B + A_b + \sqrt{A_B \cdot A_b}) $$ dove \( h \) è l'altezza del tronco, \( A_B \) è l'area della base maggiore, e \( A_b \) è l'area della base minore.Dimostrazione. Il volume del tronco di una piramide è uguale alla differenza dei volumi di due piramidi: il volume $ V_1 $ di una piramide più grande con la base maggiore ABCD e il volume $ V_2 $ di una piramide più piccola con la base minore A'B'C'D' con lo stesso vertice O.
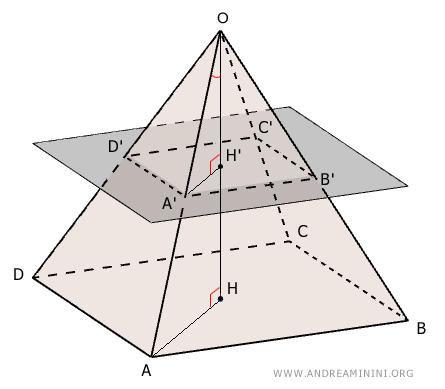
I volumi delle due piramidi sono: $$ V_1 = \frac{1}{3} ABCD \cdot OH $$ $$ V_2 = \frac{1}{3} A'B'C'D' \cdot OH' $$ Quindi, il volume del tronco piramide è la differenza: $$ V = V_1 - V_2 $$ $$ V = ( \frac{1}{3} ABCD \cdot OH ) - ( \frac{1}{3} A'B'C'D' \cdot OH' ) $$ Per semplificare considero $ S = ABCD $, $ s=A'B'C'D' $, $ x=OH' $, $ h+x= OH $ $$ V = \frac{1}{3} S \cdot (h+x) - \frac{1}{3} s \cdot x $$ $$ V = \frac{1}{3} S \cdot h + \frac{1}{3} S \cdot x - \frac{1}{3} s \cdot x $$ $$ V = \frac{1}{3} S \cdot h + \frac{1}{3} x \cdot (S-s) $$ Le due piramidi sono poligoni simili, perché il rapporto tra i lati e tra le altezze è lo stesso. Pertanto, in base al teorema delle aree dei poligono simili, le sezioni parallele di una piramide sono direttamente proporzionali ai quadrati delle loro distanze dal vertice della piramide. $$ S:s = (h+x)^2:x^2 $$ Calcolo la radice quadrata di entrambi i membri $$ \sqrt{S:s} = \sqrt{ (h+x)^2:x^2 } $$ $$ \sqrt{S} : \sqrt{s} = \sqrt{(h+x)^2} : \sqrt{x^2} $$ $$ \sqrt{S} : \sqrt{s} = (h+x) : x $$ Applico la proprietà dello scomporre di una proporzione a:b=c:d ossia (a-b):b = (c-d):d. $$ \sqrt{S} - \sqrt{s} : \sqrt{s} = (h+x) - x : x $$ $$ \sqrt{S} - \sqrt{s} : \sqrt{s} = h : x $$ Trovo la x $$ x = \frac{h \sqrt{s}}{ \sqrt{S} - \sqrt{s} } $$ Razionalizzo $$ x = \frac{h \sqrt{s}}{ \sqrt{S} - \sqrt{s} } \cdot \frac{ \sqrt{S} + \sqrt{s} }{ \sqrt{S} + \sqrt{s} } $$ $$ x = \frac{h \sqrt{s} \cdot ( \sqrt{S} + \sqrt{s} ) }{ (\sqrt{S} - \sqrt{s} ) \cdot ( \sqrt{S} + \sqrt{s} ) } $$ $$ x = \frac{h \sqrt{s} \cdot ( \sqrt{S} + \sqrt{s} ) }{ S-s } $$ Torno alla prima proporzione $$ V = \frac{1}{3} S \cdot h + \frac{1}{3} x \cdot (S-s) $$ Sostituisco la x $$ V = \frac{1}{3} S \cdot h + \frac{1}{3} \cdot \frac{h \sqrt{s} \cdot ( \sqrt{S} + \sqrt{s} ) }{ S-s } \cdot (S-s) $$ $$ V = \frac{1}{3} S \cdot h + \frac{1}{3} \cdot h \cdot \sqrt{s} \cdot ( \sqrt{S} + \sqrt{s} ) $$ $$ V = \frac{1}{3} S \cdot h + \frac{1}{3} \cdot h \cdot \sqrt{S \cdot s} + \frac{1}{3} \cdot h \cdot \sqrt{s^2}$$ $$ V = \frac{1}{3} S \cdot h + \frac{1}{3} \cdot h \cdot \sqrt{S \cdot s} + \frac{1}{3} \cdot h \cdot s $$ $$ V = \frac{1}{3} h \cdot (S + s + \sqrt{S \cdot s} ) $$ Dove $ S=A_B $ è l'area della base maggiore e $ s=A_b $ è l'area della base minore del tronco di piramide. $$ V = \frac{1}{3}h(A_B + A_b + \sqrt{A_B \cdot A_b}) $$
Note aggiuntive
Alcune note e osservazioni sul tronco di piramide.
- La sezione e la base sono simili
In un tronco di piramide la sezione e la base sono poligoni simili.Dimostrazione. La sezione e la base fanno parte di due piani paralleli \( \pi \) e \( \pi' \) che intersecano le facce della piramide. Pertanto, i segmenti della base e della sezione sono paralleli tra loro $ AB \parallel A'B $. I triangoli VAB e VA'B' hanno l'angolo al vertice $ V $ in comune.
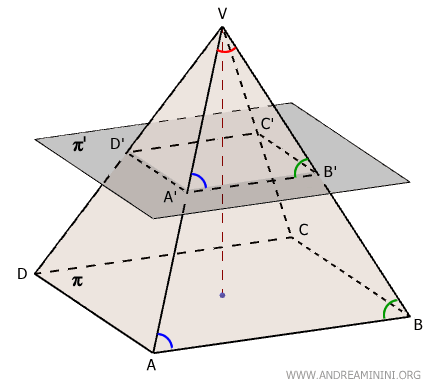
Gli angoli $ V \hat{A} B $ e $ V \hat{A'} B' $ sono congruenti per il teorema delle rette parallele, perché i segmenti $ AB $ e $ A'B' $ sono paralleli e sono tagliati dalla stessa retta trasversale a cui appartiene $ VA $. Per la stessa ragione sono congruenti anche gli angoli $ V \hat{B} A $ e $ V \hat{B'} A' $. Quindi, i triangoli $ VAB $ e $ VA'B' $ sono simili per il primo criterio di similitudine perché hanno tutti gli angoli congruenti nello stesso ordine. $$ VAB \approx VA'B' $$ Quindi, posso scrivere $$ AB:A'B' = VB : VB' $$ Allo stesso modo sono simili i triangoli nelle altre facce del triangolo: $ VBC \approx VB'C' $ , $ VCD \approx VC'D' $ , $ VAD \approx VA'D' $. Quindi, posso scrivere anche $$ BC:B'C' = VB : VB' $$ Per la proprietà transitiva ottengo: $$ AB:A'B' = VB : VB' = BC:B'C' $$ $$ AB:A'B' = BC:B'C' $$ Lo stesso ragionamento posso ripeterlo con le altre facce rimanenti della piramide. Questo dimostra che i lati corrispondenti della base e della sezione sono proporzionali e hanno gli angoli corrispondenti congruenti perché sono sezioni parallele dello stesso diedro.
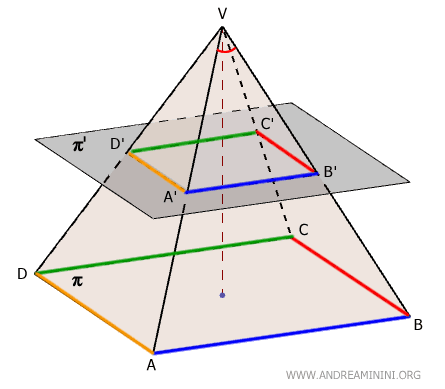
Pertanto, i poligoni nella base e nella sezione sono poligoni simili. $$ ABCD \approx A'B'C'D' $$ - I lati e i perimetri sono proporzionali alla distanza dal vertice
Se si taglia una piramide con un piano parallelo alla base, i lati e i perimetri del poligono della sezione risultante sono proporzionali alla distanza tra il loro piano e il vertice V.Dimostrazione. I triangoli VAH e VA'H' sono simili per il primo criterio di similitudine perché ha due angoli corrispondenti congruenti, l'angolo al vertice V in comune $ A \hat{V} H \cong A' \hat{V} H' $ e l'angolo retto (90°).
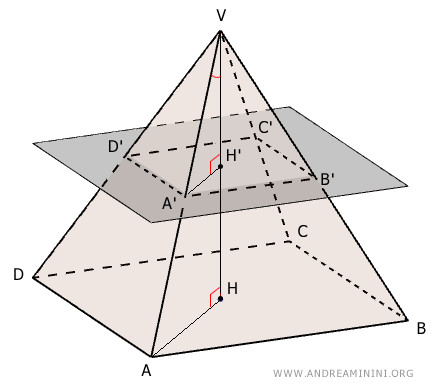
Poiché i triangoli $ VAH \approx VA'H' $ sono simili, hanno i lati omologhi con lo stesso rapporto di proporzionalità. In particolare, mi interessa sapere che: $$ VH : VH' = VA : VA' $$ Anche i triangoli ABV e A'B'V sono simili per il primo criterio di similitudine, perché hanno lo stesso angolo al vertice V e gli angoli alla base sono congruenti $ V \hat{A} B \cong V \hat{A'} B' $ per il teorema delle rette parallele,

Poiché i triangoli $ ABV \approx A'B'V $, i lati omologhi hanno lo stesso rapporto di proporzionalità. In particolare mi interessa sapere che $$ AB : A'B' = VA : VA' $$ Per la proprietà transitiva, sapendo che $ VH : VH' = VA : VA' $ deduco che $$ AB : A'B' = VH : VH' $$ Con la stessa logica deduco che anche gli altri lati dei poligoni alla base e alla sezione hanno lo stesso rapporto di proporzionalità $$ BC : B'C' = VH : VH' $$ $$ CD : C'D' = VH : VH' $$ $$ AD : A'D' = VH : VH' $$ Quindi, anche i loro perimetri hanno lo stesso rapporto di proporzionalità $ VH : VH' $ $$ (AB+BC+CD+AD) : (A'B'+B'C'+C'D'+A'D') = VH : VH' $$ Indico il perimetro con $ 2p $ e $ 2p' $ $$ 2p : 2p' = VH : VH' $$ Infine, da questo deduco ache il rapporto di proporzionalità tra i due perimetri è uguale a quello dei lati omologhi dei poligoni. $$ 2p : 2p' = AB : A'B' $$ $$ 2p : 2p' = BC : B'C' $$ $$ 2p : 2p' = CD: C'D' $$ $$ 2p : 2p' = AD : A'D' $$ - Il rapporto tra l'area della base e della sezione è uguale al quadrato del rapporto di similitudine
In una piramide troncata il rapporto tra la superficie della base S e della sezione S' è uguale al quadrato del rapporto di similitudine. \[ \frac{S}{S'} = \left( \frac{AB}{A'B'} \right)^2 = k^2 \]Dimostrazione. La base e la sezione della piramide troncata sono due poligoni simili. Il rapporto tra le aree di due poligoni simili $ \frac{S}{S'} $ è uguale al quadrato del rapporto di similitudine $ k^2 $ (vedi dimostrazione). Quindi, il rapporto tra l'area della base e della sezione in una piramide troncata è uguale al quadrato del rapporto di similitudine $ k $.
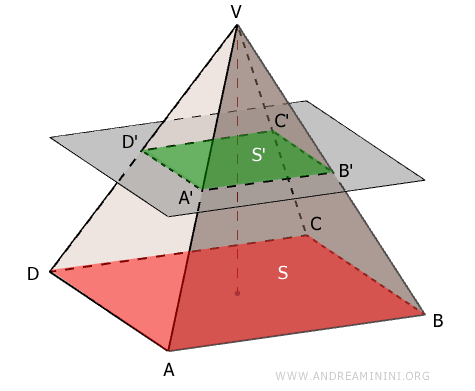
Ad esempio, considero una piramide che ha per base un quadrato, l'area della base $ ABCD $ è uguale al quadrato di un lato $ S = (AB)^2 $. Allo stesso modo l'area della sezione $ A'B'C'D' $ è il quadrato di un lato $ S'=(A'B')^2 $. Quindi il rapporto tra le superfici è il seguente $$ \frac{S}{S'} = \frac{(AB)^2}{(A'B')^2} = \left( \frac{AB}{A'B'} \right)^2 = k^2 $$ Dove $ k = \frac{AB}{A'B'} $ è il rapporto di similitudine tra i due poligoni. Questa proprietà vale per qualsiasi coppia di poligoni simili, non solo per i quadrati. Infatti, in due poligoni simili i lati corrispondenti stanno nello stesso rapporto k e anche tutte le altre dimensioni (come altezze, diagonali, ecc.) sono proporzionali con lo stesso rapporto.
E così via.
