Solidi equivalenti

Due solidi si dicono equivalenti quando hanno lo stesso volume, anche se possono avere forme completamente diverse. \[ V_A = V_B \] Dove \( V_A \) e \( V_B \) rappresentano il volume dei due solidi.

Il concetto non riguarda né la forma né l’area della superficie, ma solo la quantità di spazio occupato all’interno del solido.

Due oggetti possono apparire completamente diversi, ma occupare lo stesso spazio.

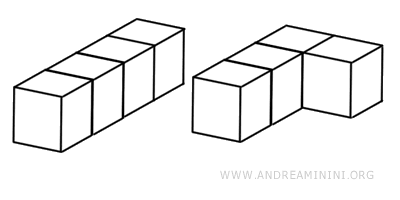
Dunque, l’equivalenza non implica che i solidi abbiano la stessa altezza, base o superficie laterale, ma solo uguale quantità di materia (volume).

Un esempio pratico

Un cubo con lato 3 cm ha un volume di 3 cm³:

\[ V = 3^3 = 27 \ cm^3 \]

Un parallelepipedo con base 3 cm × 3 cm e altezza 3 cm ha lo stesso volume (3 cm³).

\[ V = 3^3 = 27 \ cm^3 \]

E anche un cilindro con base di area 9 cm² e altezza 3 cm ha lo stesso volume:

\[ V = 9 \cdot 3 = 27 \ cm^3 \]

Sono solidi diversi ma equivalenti.

Le trasformazioni dei solidi equivalenti

Molti solidi possono essere trasformati l’uno nell’altro senza cambiare il volume.

Queste trasformazioni si basano su spostamenti, tagli e ricomposizioni.

Esempio

Un prisma a base triangolare può essere scomposto in tre piramidi equivalenti che posso combinare in modo diverso e ottenere un solido equivalente al prisma iniziale.

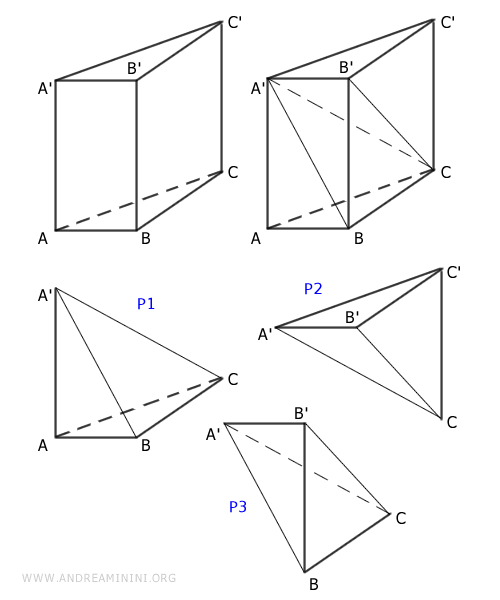
Nota. Le piramidi P1 e P2 hanno la base congruente $ ABC = A'B'C' $ e l'altezza congruente $ AA' = CC' $. Quindi, sono equivalenti. Le piramidi P2 e P3 hanno la base congruente $ BCC' = BCB' $ e l'altezza in comune $ A'B' $, quindi sono equivalenti. Infine, per la proprietà transitiva anche P1 e P3 sono equivalenti.

Il volume di una piramide si calcola con la seguente formula:

\[ V = \frac{1}{3} \cdot \text{base} \cdot \text{altezza} \]

La formula del volume del prima è, invece, la seguente:

\[ V = \text{base} \cdot \text{altezza} \]

Questo significa che,  se la base e l’altezza sono coerenti, il volume della piramide è un terzo di quello del prisma.

Quindi, se metto insieme tre piramidi identiche, ottengo un prisma equivalente. Questo dimostra che i due solidi sono equivalenti.

Differenza tra equivalenza e congruenza

Non bisogna confondere il concetto dell'equivalenza con la congruenza.

• Congruenza: i solidi hanno stessa forma e dimensione. Ad esempio, due cubi identici sono congruenti e quindi anche equivalenti.
  
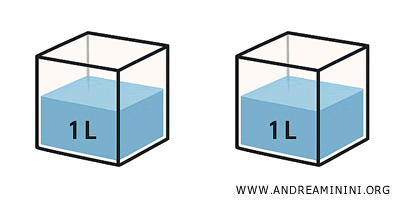
• Equivalenza: i solidi hanno solo stesso volume. Ad esempio, un cubo e un cilindro con stesso volume sono equivalenti, ma non congruenti.
  

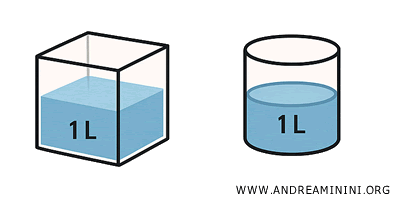
In altre parole, "congruente" significa uguale in tutto: forma, dimensione e volume, mentre "equivalente" significa solo che hanno lo stesso volume ma le forme possono essere diverse.

Quindi "equivalente" non significa che due solidi si possono sovrapporre o che sono identici: solo che occupano la stessa quantità di spazio.

Note

Alcune note aggiuntive e osservazioni personali sull'equivalenza tra solidi.

• La somma o la differenza di solidi congruenti o equivalenti genera solidi equivalenti
  Se costruisco un solido unendo (sommando) o togliendo (sottraendo) solidi che sono congruenti (cioè uguali in forma e dimensione) o equivalenti (cioè con lo stesso volume), allora i solidi ottenuti avranno lo stesso volume, cioè saranno equivalenti (in senso volumetrico).
  

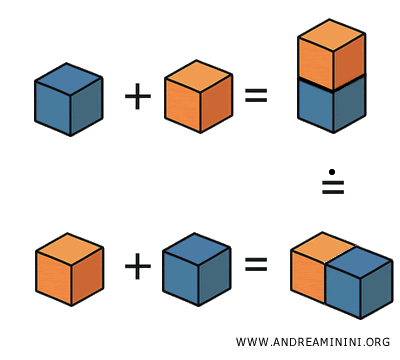
  Esempio. Se ho due cubi uguali e tolgo una piramide uguale in entrambi, i solidi che rimangono sono equivalenti. Se gli stessi due solidi aggiungo lo stesso cilindro, i risultati avranno lo stesso volume, quindi saranno equivalenti.

• Legge di esclusione
  Secondo questo postulato (detto legge di esclusione) dati due solidi A e B, esistono tre casi possibi:
  • A e B sono equivalenti $ A \doteq B $ ossia A e B hanno lo stesso volume
  • A è prevalente a B ossia $ A>B $. In questo caso A ha un volume maggiore di B.
  • A è suvvalente a B ossia $ A<B $. In questo caso A ha un volume minore di B.
  Ogni caso esclude gli altri.

  Nota. La classificazione proposta (equivalente, prevalente, subvalente) presuppone che ogni coppia di solidi sia sempre confrontabile in modo univoco. Tuttavia, trascura l’eventualità, tutt’altro che rara, che due elementi non siano confrontabili secondo un solo criterio, per via di caratteristiche multiple o incommensurabili (volume, simmetria, complessità computazionale, estetica, ecc.). La presenza di più criteri non garantisce affatto la possibilità di stabilire una relazione d’ordine. Spesso, dunque, il confronto è impossibile, e ridurre ogni relazione a un ordinamento totale rischia di appiattire la complessità della realtà. Ad esempio, un cubo di marmo e uno di legno possono avere lo stesso volume, ma restano incomparabili per peso, densità, costo, resistenza o significato d’uso. Allo stesso modo, una sfera e un cubo di pari volume differiscono per superficie, aerodinamica e stabilità, cioè per tutte le proprietà che contano oltre la semplice misura. Pretendere di ridurre simili differenze a un singolo criterio equivale a cancellare la complessità con una scorciatoia arbitraria.

• Postulato di De Zolt
  Secondo il postulato di De Zolt un solido non può essere equivalente a una sua parte. Questo vuol dire che non può avere lo stesso volume di una sua parte, cioè una porzione strettamente contenuta al suo interno.
• Principio di Cavalieri
  Se per ogni piano parallelo in una determinata direzione le sezioni ottenute intersecando i solidi hanno uguale area, allora i solidi hanno lo stesso volume.

E così via.