Solidi equicomposti

Due solidi si dicono equicomposti (o equiscomponibili) se è possibile suddividerli in un numero finito di parti solide, in modo che ogni parte di un solido sia congruente alla corrispondente parte dell’altro. A condizione che i pezzi siano solidi geometrici, non superfici né linee.

In parole semplici: due solidi sono equicomposti se li posso “smontare” in pezzi che coincidono esattamente con quelli dell’altro, senza lasciare residui e senza doverli deformare.

Ogni parte del primo solido deve essere uguale in forma e dimensioni alla corrispondente parte dell’altro solido.

La ricomposizione non richiede né allungamenti né compressioni: è una ricostruzione geometrica perfetta.

I solidi equicomposti hanno necessariamente lo stesso volume, perché ogni pezzo corrisponde a uno stesso spazio.

Nota. Il contrario non è sempre vero. Due solidi con lo stesso volume non sono necessariamente equicomposti.

Esempio pratico

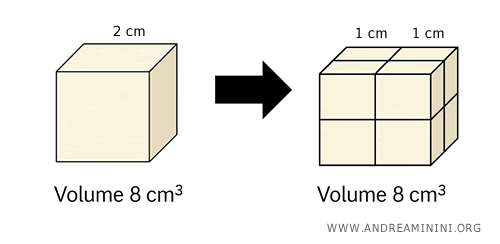
Considero un cubo di lato 2 cm che ha un volume di 8 cm³.

Immagino ora un altro cubo dello stesso volume, ottenuto scomponendo il primo in otto cubetti di lato 1 cm.

Se prendo questi otto cubetti e li riordino per formare un altro cubo, ottengo un cubo equicomposto a quello iniziale.

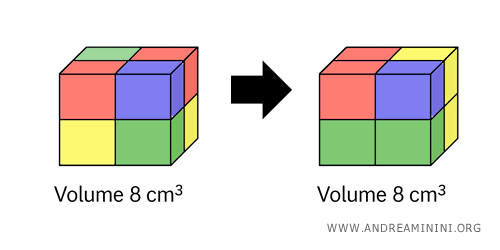
In questo caso, i due solidi sono equicomposti, perché composti dagli stessi otto cubetti congruenti.

Inoltre, sono solidi equivalenti, perché hanno lo stesso volume.

Esempio 2

Considero due prismi rettangolari con base quadrata:

Il primo prisma ha lato di base 2 cm e altezza 3 cm.

Il secondo prisma ha lato di base 1 cm e altezza 12 cm.

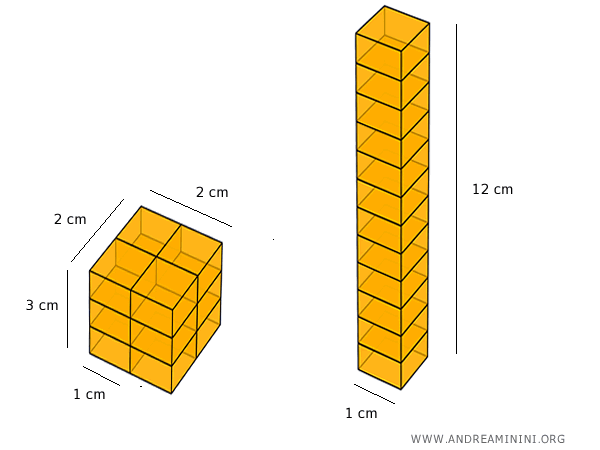
Entrambi i solidi hanno un volume di 12 cm³ e sono equiscomponibili perché posso dividerli in blocchi congruenti senza tagli complessi.

Esempio 3

Considero una piramide con base quadrata con lato di base di 1 cm e altezza di 3 cm e  un cubo di lato 1 cm.

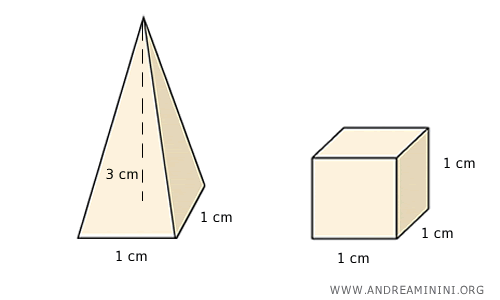
La piramide ha un volume di 1 cm³

$$ V_p = \frac{1}{3} l^2 \cdot h = \frac{1}{3} \cdot (1 \ cm)^2 \cdot 3 \ cm = 1 \ cm^3 $$

Anche il volume del cubo è 1 cm³

Tuttavia, una piramide regolare con base quadrata e un prisma a base quadrata possono avere lo stesso volume, ma non essere equiscomponibili.

Infatti, non esiste un modo per scomporre una piramide in un numero finito di solidi congruenti a quelli di un prisma, a meno di considerazioni teoriche molto complesse e fuori dall’ambito della geometria elementare.

Quindi, due solidi possono avere stesso volume, ma non sono equicomposti secondo la definizione.

Differenza tra solidi equivalenti ed equicomposti

 In geometria, essere equicomposti è una condizione più restrittiva rispetto all’equivalenza.

• I solidi equivalenti hanno lo stesso volume, ma non necessariamente una relazione geometrica più profonda.
• I solidi equicomposti sono anche equivalenti, hanno lo stesso volume, ma possiedono un vincolo geometrico più forte: possono essere divisi e ricomposti tramite pezzi solidi congruenti.

Il concetto di equicomposizione è un raffinato strumento della geometria, perché va oltre il semplice calcolo del volume.

Richiede di pensare lo spazio come componibile e ricomponibile, come un puzzle tridimensionale.

Nota. In geometria solida classica, dimostrare che due solidi sono equicomposti non è banale, ed è una questione di struttura geometrica interna, non solo di misura esterna.

Teorema dell’Equicomponibilità

Se due solidi sono equicomposti, allora sono anche equivalenti, cioé hanno lo stesso volume.

In altre parole l’equicomposizione implica l'equivalenza tra i solidi.

Il teorema non vale in senso inverso: due solidi possono avere lo stesso volume (essere equivalenti) senza essere equicomposti, come avviene per una sfera e un cubo.

Quindi, essere equicomposti è una relazione forte: non basta avere lo stesso volume, bisogna anche poter “ricomporre” un solido nell’altro usando parti congruenti.

Nota. Se prendo dei mattoncini giocattolo e costruisco una parete. Poi smonto tutto e con gli stessi mattoncini costruisco una torre. I due oggetti hanno forma diversa, ma sono fatti dagli stessi pezzi. In geometria solida, si dice che le due costruzioni sono equicomposte. Poiché i mattoncini hanno sempre lo stesso volume, anche la torre avrà lo stesso volume del muro. Quindi i due solidi sono equivalenti in volume.

Fu Euclide, negli Elementi (Libro XII), a introdurre formalmente il concetto, anche se non in termini moderni.

L’idea venne poi sviluppata da matematici rinascimentali e formalizzata da Bonaventura Cavalieri, che studiò il concetto di sezioni equiestese, arrivando al suo celebre "principio di Cavalieri".

Esempio Pratico

Considero i due solidi $\mathbb{U}$ e $\mathbb{V}$, rappresentati nella figura sottostante (non inclusa qui).

Il solido $\mathbb{U}$ è composto da tre parti: $\mathbb{U}_1$, $\mathbb{U}_2$ e $\mathbb{U}_3$.

Il solido $\mathbb{V}$ è anch’esso composto da tre parti: $\mathbb{V}_1$, $\mathbb{V}_2$ e $\mathbb{V}_3$.

Suppongo che:

$\mathbb{U}_1 \cong \mathbb{V}_1$ (sono congruenti),

$\mathbb{U}_2 \cong \mathbb{V}_2$,

$\mathbb{U}_3 \cong \mathbb{V}_3$.

Dato che ciascuna parte di $\mathbb{U}$ è congruente alla parte corrispondente di $\mathbb{V}$, posso concludere che i due solidi sono equicomposti.

 

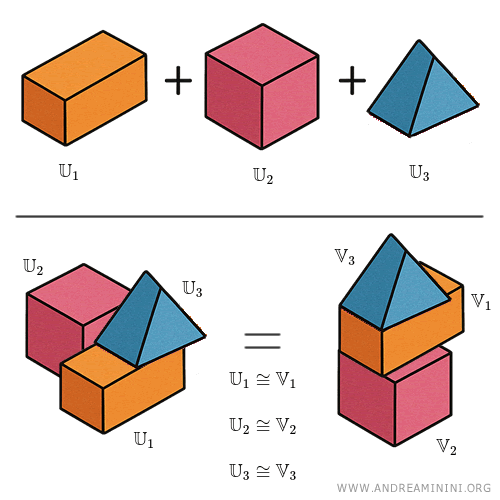
Secondo il teorema enunciato, i due solidi risultano anche equivalenti, poiché occupano lo stesso volume nello spazio, pur presentando forme complessive diverse.

L’invariante di Dehn

In geometria solida, avere lo stesso volume non basta per garantire che due solidi siano equicomposti.

Il motivo profondo sta in una quantità matematica chiamata invariante di Dehn, introdotta nel 1900 dal matematico tedesco Max Dehn. E' il vero ostacolo all’equicomposizione nei solidi.

L’invariante di Dehn tiene conto degli angoli diedri (cioè gli angoli tra le facce dei solidi) e del modo in cui questi angoli si combinano all’interno della figura.

Se due poliedri hanno invarianti di Dehn diversi, allora non sono equicomponibili.

Questo teorema dimostra che non esiste un procedimento di taglio e ricomposizione (con pezzi solidi congruenti) che trasformi, ad esempio, un cubo in un tetraedro di uguale volume, perché hanno invarianti di Dehn diversi.

In pratica:

• Nel piano (2D) due poligoni di pari area sono equicomponibili (Teorema di Bolyai - Gerwien).
• Nello spazio (3D), invece, entra in gioco l’invariante di Dehn, e la festa finisce.

Questa è la frontiera dell’equicomposizione, o perlomeno una delle prime frontiere, poiché ci sono anche problemi più profondi, legati alla teoria delle misure, alle decomposizioni non misurabili, al concetto stesso di congruenza in spazi più generali.

Note

Alcune osservazioni, approfondimenti e note aggiuntive sull'equicomposizione

• Paradosso di Banach-Tarski
  Il paradosso di Banach-Tarski afferma che in certe condizioni teoriche, assumendo l’assioma della scelta, una sfera solida può essere suddivisa in un numero finito di sottoinsiemi tali da poter essere ricomposti, mediante sole rotazioni e traslazioni, in due sfere identiche all’originale. Il che sembra assurdo.

  Nota. Questo risultato non viola la geometria classica: la aggira. I “pezzi” in questione non sono solidi reali, né geometricamente descrivibili: sono insiemi non misurabili, privi di volume, costruiti in modo puramente teorico. Per questo motivo Banach-Tarski non rappresenta un esempio valido di equicomposizione. Non coinvolge parti congruenti, non conserva la misura, e opera fuori dal dominio delle dissezioni geometriche classiche. È una dimostrazione estrema di ciò che accade quando si spinge la teoria degli insiemi oltre ogni confine intuitivo.

E così via.