Piramidi
Una piramide è un poliedro formato dall'intersezione di un angoloide con un piano che taglia tutti i suoi spigoli. La sezione di questa intersezione è conosciuta come base della piramide, e può assumere varie forme poligonali. Il vertice dell'angoloide è invece il vertice della piramide.
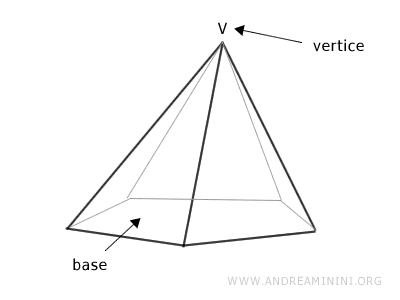
La base della piramide è un poligono mentre le facce laterali sono dei triangoli.
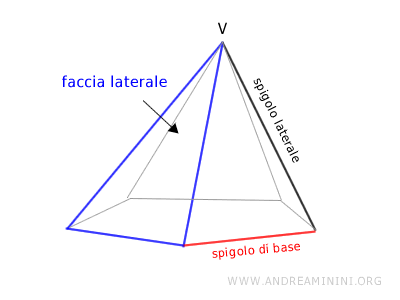
I lati che delimitano la base sono detti spigoli di base, mentre gli spigoli che congiungono la base al vertice sono gli spigoli laterali.
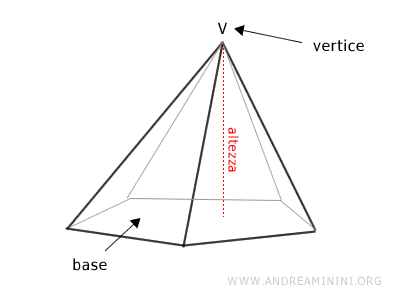
Una caratteristica fondamentale della piramide è l'altezza, ovvero la distanza perpendicolare dal vertice al piano su cui giace la base.
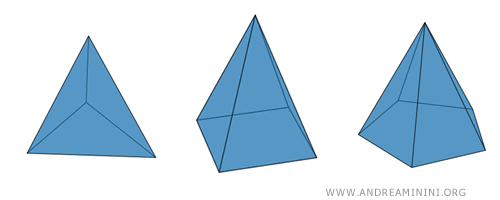
A seconda dei lati della base, una piramide è detta triangolare, quadrangolare, pentagonale, ecc.
In ogni piramide il numero dei vertici coincide con il numero delle facce compresa la base. Inoltre, una piramide non può avere meno di quattro facce. La piramide con minor numero di facce è il tetraedro ed è composta da quattro triangoli.
Tipi di piramidi
Esistono diversi tipi di piramidi
- Piramide su base triangolare o quadrata
Il poligono di base della piramide può essere un triangolo, un quadrilatero o un qualsiasi altro poligono regolare o irregolare. Se la base è un triangolo la piramide è detta triangolare, se è un quadrato si dice piramide su base quadrata, se invece è un quadrilatero è detta piramide quadrangolare, ecc.
- Piramide retta
Una piramide si definisce piramide retta quando la base ABCD della piramide è inscrivibile in una circonferenza e il vertice della piramide (V) è perpendicolare al centro della circonferenza (O) circoscritta alla base.
In altre parole, il vertice della piramide è la proiezione ortogonale del centro della circonferenza in cui è inscritta la base della piramide. Nelle piramidi rette l'altezza della piramide cade perpendicolarmente al centro (O) della base (segmento OV). Le altezze sulle facce laterali di una piramide retta sono dette apotemi.
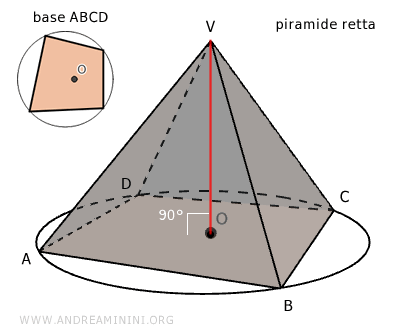
In alternativa, si può anche dire che una piramide è retta se nella base si può inscrivere una circonferenza, il cui centro O è la proiezione ortogonale del vertice V della piramide sul piano della base.
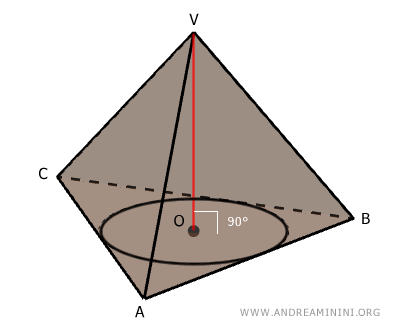
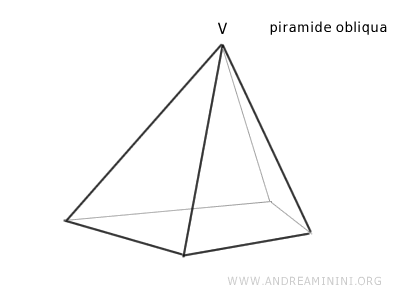
Tutte le piramidi che non sono rette sono dette piramidi oblique.
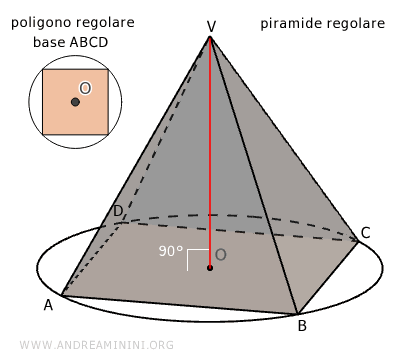
- Piramide regolare
Una piramide regolare è una piramide retta che ha per base ABCD un poligono regolare.
Essendo un poligono regolare, la base della piramide è sempre inscrivibile e circoscrivibile a una circonferenza. Di conseguenza, tutte le facce laterali della piramide sono triangoli isosceli congruenti e hanno tutte la stessa altezza (apotema). Inoltre, essendo una piramide retta, l'altezza della piramide cade al centro (O) della base (segmento OV).
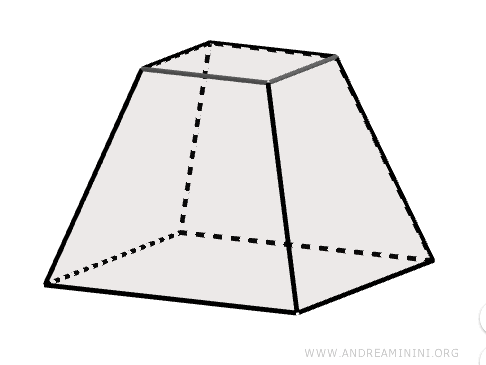
- Tronco di piramide
Il tronco di piramide è una figura geometrica solida ottenuta sezionando una piramide con un piano parallelo alla base.
Teorema degli apotemi di una piramide retta
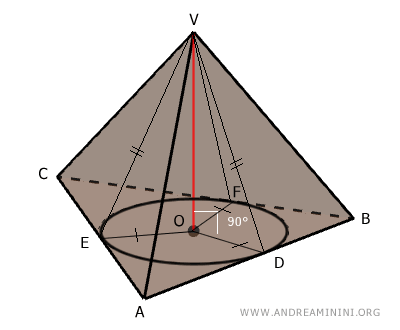
In una piramide retta, le altezze delle facce laterali (apotemi) sono congruenti VD≅VE≅VF e passano per i punti di tangenza D, E, F dei lati della base con la circonferenza inscritta.
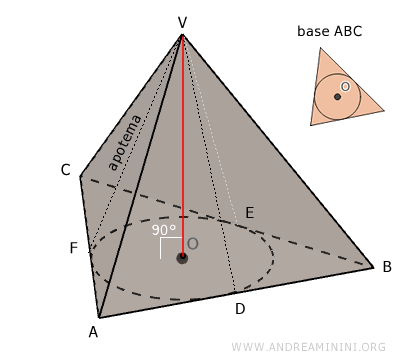
Nell'esempio precedente gli apotemi sono i segmenti VD, VE, VF e sono tra loro congruenti.
$$ \overline{VD} \cong \overline{VE} \cong \overline{VF} $$
Questo risultato è utile nella determinazione delle proprietà metriche delle piramidi.
Le formule
Il volume di una piramide
Il volume \( V \) di una piramide è dato dalla formula:
$$ V = \frac{1}{3} \cdot (\text{area della base}) \cdot (\text{altezza}) $$
Questa formula si applica indipendentemente dalla forma della base.
Pertanto, il calcolo del volume di una piramide è abbastanza semplice, purché si conoscano l'area della base e l'altezza della piramide.
Nota. Il volume della base è un terzo del prodotto tra l'area della base per l'altezza, perché qualsiasi piramide è equivalente alla terza parte di un prisma che ha la stessa base e la stessa altezza. Vedi solidi equivalenti.
La superficie laterale
La superficie laterale di una piramide è la somma delle superfici delle facce laterali.
Nel caso di una piramide regolare, la superficie laterale è uguale al semiperimetro (p) della base per l'apotema (a)
$$ A_L = p \cdot a $$
La superficie totale
La superficie totale di una piramide è la somma delle superfici di tutte le facce della piramide (compresa la base).
$$ A = A_L + A_B $$
Dove AL è la superficie laterale mentre AB è l'area della base.
Esempio. Nel caso di una piramide retta su base quadrangolare, lo sviluppo della piramide consiste in un quadrato (base) e quattro triangoli di uguale altezza pari all'apotema (a).
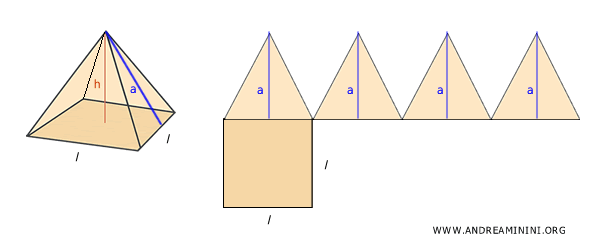
Quindi, l'area laterale della piramide è $$ A_l = \frac{1}{2} l \cdot a + \frac{1}{2} l \cdot a + \frac{1}{2} l \cdot a + \frac{1}{2} l \cdot a $$ $$ A_l = 4 \cdot \frac{1}{2} l \cdot a $$ Sapendo che $ P=4l $ è il perimetro della piramide. $$ A_l = \frac{1}{2} P \cdot a $$ E che $ p= \frac{1}{2} P $ è il semiperimetro. $$ A_l = p \cdot a $$ Quindi, l'area laterale è il semiperimetro per l'apotema. L'area totale, invece, è semplicemente la somma della superficie laterale e quella di base. $$ A_t = A_b + A_l = A_b + p \cdot a $$
Osservazioni
Alcune osservazioni e note a margine sulle piramidi.
- Tronco di piramide
Un piano parallelo alla base che interseca la piramide all'altezza h, la divide in due parti: la parte superiore è ancora una piramide A'B'C'V mentre la parte inferiore è un tronco di piramide di altezza h.
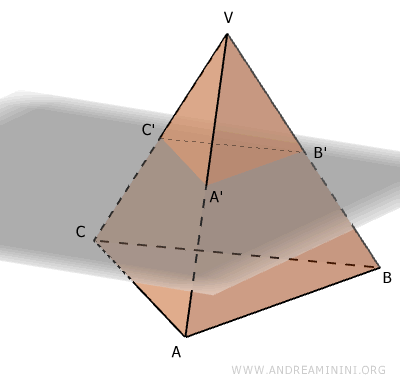
- Teorema delle altezze delle facce laterali di una piramide retta
In una piramide retta le altezze delle facce laterali (apotemi) sono tra loro congruenti e passano per i punti di tangenza tra la circonferenza inscritta e i lati della base della piramide.
- Piramidi equivalenti in volume
Due piramidi che hanno basi con la stessa area e altezze congruenti (cioè uguali) sono equivalenti in volume. In altre parole, se due piramidi hanno la stessa area di base $ A_b $ e la stessa altezza $ h $, allora hanno anche lo stesso volume indipendetemente dalla forma.
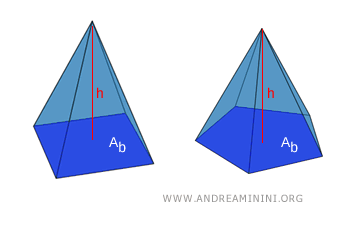
Dimostrazione. Questa proprietà deriva dalla formula del volume della piramide: $$ V = \frac{1}{3} \cdot \text{area della base} \cdot \text{altezza} $$ Poiché il volume della piramide dipende solo da questi due fattori (area di base e altezza), due piramidi con gli stessi valori in questi parametri avranno lo stesso volume.
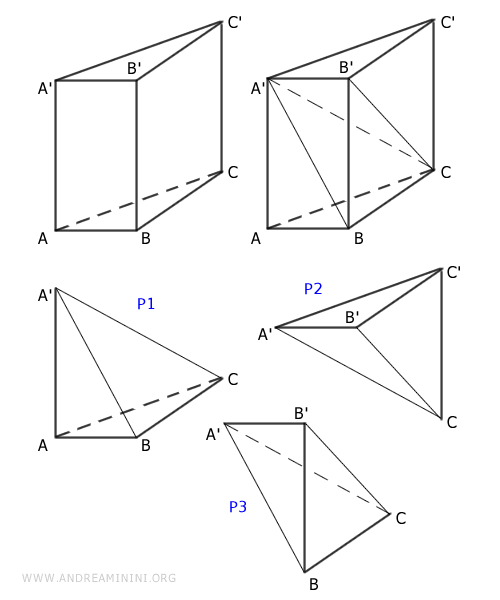
- Una piramide è equivalente alla terza parte di un prisma con la stessa base e la stessa altezza
Se una piramide e un prisma hanno le basi congruenti e le altezze congruenti, allora la piramide è equivalente a un terzo del volume del prisma.Esempio. Un prisma a base triangolare ABC posso scomporlo in tre piramidi equivalenti P1, P2, P3.

Le piramidi P1 e P2 hanno la base congruente $ ABC \cong A'B'C' $ e l'altezza congruente $ AA' \cong CC' $. Quindi, sono piramidi equivalenti in volume. $$ P1 \doteq P2 $$ Le piramidi P2 e P3 hanno la base congruente $ BCC' \cong BCB' $ e l'altezza in comune $ A'B' $, quindi sono equivalenti in volume. $$ P2 \doteq P3 $$ Per la proprietà transitiva anche le piramidi P1 e P3 sono equivalenti in volume. $$ P1 \doteq P2 \doteq P3 \Rightarrow P1 \doteq P3 $$ Pertanto, le tre piramidi che compongono il prisma hanno lo stesso volume. Sapendo che il volume di una piramide si calcola con la formula: \[ V = \frac{1}{3} \cdot \text{base} \cdot \text{altezza} \] mentre il volume del prisma si calcola con la formula: \[ V = \text{base} \cdot \text{altezza} \] è subito evidente che se i due solidi hanno la base e l'altezza congruenti, allora il volume della piramide è esattamente un terzo del volume del prisma. - Equivalenza in volume tra piramide e cono
Una piramide e un cono che hanno basi equivalenti (cioè con la stessa area) e altezze congruenti (cioè della stessa misura) sono equivalenti in volume. In altre parole, se la base della piramide ha la stessa area della base del cono e l'altezza è identica, allora il volume delle due figure è lo stesso.Questo principio si basa sul fatto che la formula del volume è analoga per entrambe le figure: $$ V = \frac{1}{3} \cdot \text{area di base} \cdot \text{altezza} $$ Quindi, a parità di base e altezza, il volume è identico.Dimostrazione. Considero una piramide e un cono appoggiati sullo stesso piano $ \alpha $, con area di base uguale ($ S = S' $) e altezza congruente ($ AB \cong CD $).
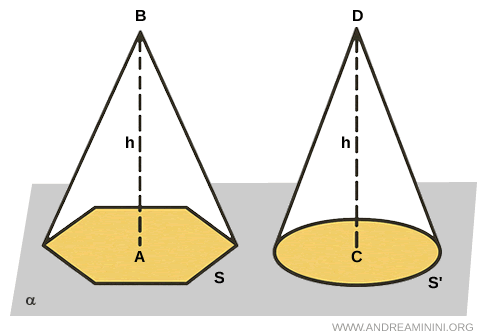
Per confrontare i due solidi, considero un altro piano $ \alpha' $ parallelo alla base ($ \alpha' \parallel \alpha $), che interseca la piramide e il cono in due sezioni parallele alle basi. Indichiamo con $ S_p $ l’area della sezione della piramide, e con $ S_c $ quella del cono.
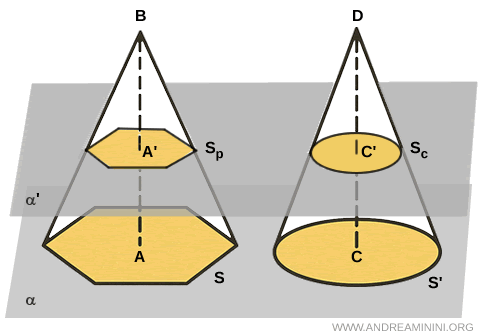
In base alle proprietà dei solidi a base poligonale e circolare (es. tronco di piramide e tronco di cono) con piani paralleli alle basi, il rapporto tra la superficie di base $ S $ e della sezione $ S_p $ è uguale al quadrato del rapporto di similitudine. $$ \frac{S}{S_p} = \left( \frac{AB}{A'B} \right)^2 \quad \text{(piramide)} $$ $$ \frac{S'}{S_c} = \left( \frac{CD}{C'D} \right)^2 \quad \text{(cono)} $$ Ma per ipotesi $ AB = CD $ e $ S = S' $, quindi: $$ \frac{S}{S_c} = \left( \frac{AB}{C'D} \right)^2 \quad \text{(cono)} $$ E poiché $ A'B = C'D $, anche i rapporti di similitudine sono uguali. $$ \frac{S}{S_c} = \left( \frac{AB}{A'B} \right)^2 \quad \text{(cono)} $$ Dunque, le due sezioni $ S_p $ e $ S_c $ hanno la stessa area: $$ \frac{S}{S_p} = \frac{S}{S_c} \quad \Rightarrow \quad S_p = S_c $$ Questo vale per ogni piano parallelo alla base, cioè ogni sezione orizzontale della piramide e del cono ha la stessa area. Poiché ogni sezione parallela alle basi ha la stessa area in entrambi i solidi, allora per il principio di Cavalieri, la piramide e il cono hanno lo stesso volume.
E così via.
