Teorema di Talete nello spazio
Un fascio di piani paralleli \( \pi_1, \pi_2, \pi_3 \) interseca due trasversali \( r \) e \( s \) determinando sulle rette dei segmenti corrispondenti proporzionali.
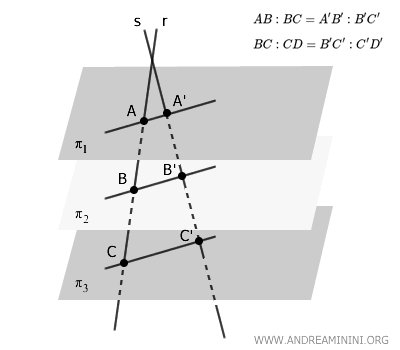
Questo teorema è semplicemente un'estensione nello spazio del classico teorema di Talete nel piano.
In sostanza, il teorema di Talete nello spazio afferma che le proporzioni tra segmenti determinati da piani paralleli si conservano su qualsiasi coppia di trasversali (sghembe o complanari).
La dimostrazione
Consideriamo un insieme di piani \( \pi_1, \pi_2, \dots, \pi_n \) paralleli tra loro.
La dimostrazione va divisa in due parti, una se le rette trasversali sono complanari e l'altra se sono sghembe.
1] Caso delle trasversali complanari
In questo caso ci sono due rette trasversali \( r \) e \( s \) complanari.
Il piano formato da \( r \) e \( s \) interseca i piani paralleli lungo rette parallele, determinando i segmenti $ AA' $, $ BB' $, $ CC' $, ecc.
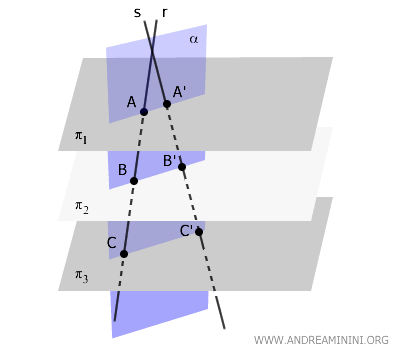
Tutte le rette parallele $ AA' \parallel BB' \parallel CC' $ sono complanari perché appartengono allo stesso piano $ \alpha $ formato dalle trasversali \( r \) e \( s \).
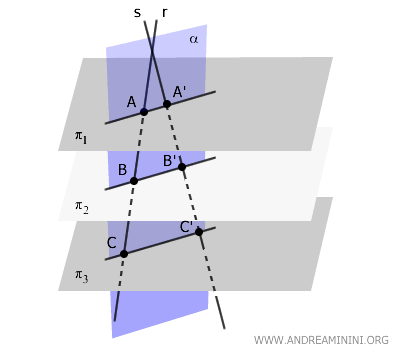
Secondo il teorema di Talete del piano, due trasversali che attraversano un fascio di rette parallele generano segmenti proporzionali.
$$ AB : BC = A'B' : B'C' $$
$$ BC : CD = B'C' : C'D' $$
$$ AC : BC = A'C' : B'C' $$
$$ ... $$
Analogamente, la proporzionalità si conserva per qualsiasi altra coppia di segmenti determinati dai piani.
Il teorema di Talete nello spazio è stato dimostrato per le trasversali complanari.
2] Caso delle trasversali sghembe
In questo caso le rette \( r \) e \( s \) sono sghembe
Indico i punti di intersezione con i piani di \( r \) con A, B, C ... e quelli di \( s \) con A', B', C'
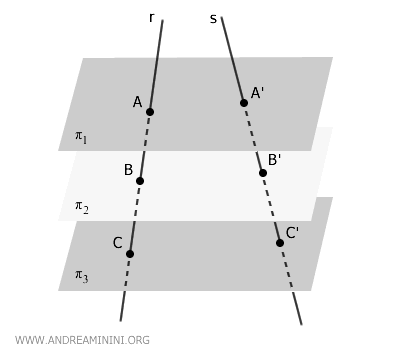
Introduco una retta \( r′′ \), parallela a \( r \) e passante per un punto \( P \) su \( s \), in modo da costruire un nuovo piano contenente \( s \) e \( r′′ \). Così posso applicare il teorema di Talete nel piano.
Indico i punti di intersezione di \( r'' \) e i piani con le lettere A'', B'', C'.
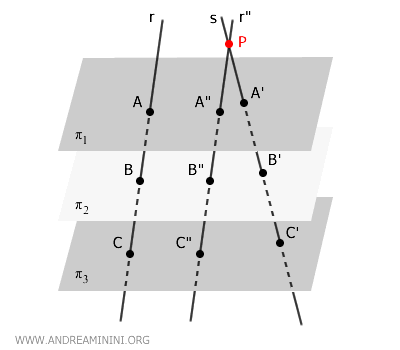
In questo modo ottengo dei parallelogrammi tra i piani come ABB"A", ACC"A", ecc.
Essendo parallelogrammi, i lati opposti sono paralleli. Quindi $ AB \cong A''B'' $, $ AC \cong A''C'' $, sono congruenti ossia uguali in lunghezza.
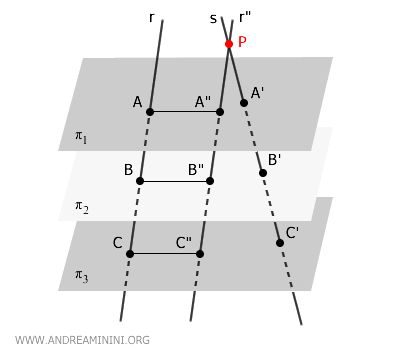
Le trasversali \( r'' \) e \( s \) sono incidenti e, quindi, appartengono allo stesso piano \( \alpha \) e sono rette complanari.
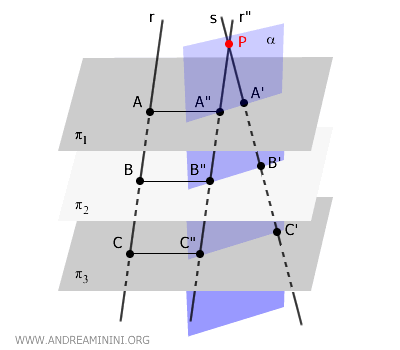
Pertanto, posso applicare alle trasversali \( r'' \) e \( s \) il teorema di Talete del piano.
$$ A''B'':B''C'' = A'B':B'C' $$
$$ A''C'':B''C'' = A'C':B'C' $$
Sapendo che i segmenti $ AB \cong A''B'' $, $ AC \cong A''C'' $, ecc. sono congruenti.
$$ AB:BC = A'B':B'C' $$
$$ AC:BC = A'C':B'C' $$
Il teorema nello spazio è stato dimostrato anche se le trasversali sono sghembe.
E così via.
