Il principio di Cavalieri

Due solidi hanno lo stesso volume se, per ogni piano parallelo in una determinata direzione (di solito orizzontale), l'area della sezione che si ottiene intersecando il primo solido è uguale a quella che si ottiene intersecando il secondo solido. 

Questo principio è utile per calcolare il volume di solidi difficili da trattare con le formule classiche.

Se riesco a dimostrare che ogni sezione di un solido ha la stessa area di una sezione corrispondente in un altro solido, posso concludere che i due solidi sono solidi equivalenti in volume, anche se hanno forme molto diverse.

Non è necessario che i solidi siano identici o simmetrici.

Esempio. Immagino due pile di fogli perfettamente rettangolari e sovrapposti, identici in numero e in forma. Se ogni foglio ha le stesse dimensioni, le due pile saranno congruenti: stesso volume, stessa forma, stessa altezza. Ma se faccio scorrere lateralmente i fogli di una delle pile, ottenendo così un solido inclinato (come una pila storta), l'intuito mi dice che il volume non cambia. Stessa altezza, stessi “strati”, dunque stessa quantità di spazio occupato.

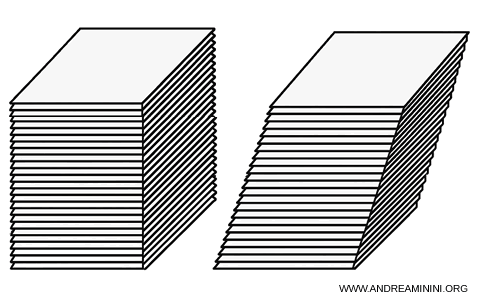
Questa idea, tanto semplice quanto rivoluzionaria, venne introdotta da Bonaventura Cavalieri nel XVII secolo ed è noto come Principio di Cavalieri.

Un limite del principio di Cavalieri

Il principio di Cavalieri fornisce una condizione sufficiente ma non necessaria.

Se le sezioni sono equivalenti, allora i solidi hanno lo stesso volume.

Ma il contrario non è sempre vero: possono esistere solidi con lo stesso volume che non soddisfano il principio di Cavalieri.

Esempio. Due solidi con volume uguale potrebbero avere sezioni diverse. In altre parole, può accadere che i solidi equivalenti non possono essere “allineati” in modo che le sezioni a ogni altezza corrispondano, pur avendo lo stesso volume. Ad esempio, questi due solidi hanno lo stesso volume ma non soddisfano il principio di Cavalieri.

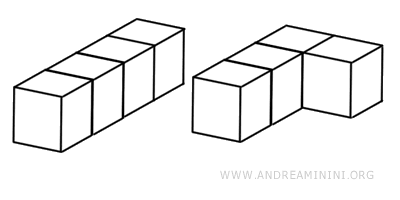
Questo lo rende matematicamente zoppo: è un principio che non caratterizza l'equivalenza di volume, ma si limita a fornire solo un indizio.

In altre parole, si tratta di un approccio parziale spacciato per esaustivo. Cavalieri ignora la complessità spaziale, e riduce la tridimensionalità a una sequenza bidimensionale.

È come se pretendessi di dire che due romanzi sono identici perché, leggendo una frase a caso da ciascuno, trovo la stessa lunghezza.

Nota. Va però detto che nel contesto storico di Cavalieri, l'idea appare brillante per mancanza di alternative. Nel XVII secolo non esiste un vero linguaggio analitico per trattare il concetto di volume in modo generale. Quindi, il principio di Cavalieri sembra giustamente una svolta perché il terreno è completamente sterile. L'intero edificio si rivela con tutti i suoi limiti appena arrivano strumenti più solidi come il calcolo integrale e la topologia.

Note

Alcune note a margine e osservazioni personali sul principio di Cavalieri

• Il calcolo integrale
  Il Principio di Cavalieri è un antenato geometrico dell’integrazione: confrontare sezioni corrisponde a sommare aree infinitesimali, proprio come si fa in un integrale. La sua “Geometria degli indivisibili” anticipa il concetto di somma continua su cui si basa l’integrale definito.
• La versione bidimensionale del principio di Cavalieri
  Due figure piane hanno la stessa area se, per ogni retta parallela in una direzione fissata, la lunghezza del segmento che ottengo intersecando la prima figura è uguale a quella del segmento che ottengo intersecando la seconda figura.

E così via.