Le proprietà delle proporzioni
In matematica le proprietà delle proporzioni sono strettamente legate alle proprietà delle frazioni.
Proprietà fondamentale delle proporzioni
In una proporzione a:b=c:d il prodotto dei termini medi di una proporzione è uguale al prodotto dei termini estremi. $$ a:b = c:d \Longleftrightarrow a \cdot d =b \cdot c $$
Questa proprietà deriva dal prodotto in croce delle frazioni equivalenti.
Una proporzione è un'uguaglianza tra frazioni equivalenti
$$ a:b = c:d \Longleftrightarrow \frac{a}{b} = \frac{c}{d} $$
Una frazione è equivalente solo se il prodotto in croce del numeratore della prima frazione per il denominatore della seconda frazione è uguale al prodotto tra il numeratore della seconda frazione per il denominatore della prima prazione.
$$ \frac{a}{b} = \frac{c}{d} \Longleftrightarrow a \cdot d =b \cdot c $$
La proprietà è detta "fondamentale" perché da questa derivano anche tutte le altre proprietà delle proporzioni.
Esempio. Considero la proporzione $$ 2:8 = 3:12 $$ Riscrivo la proporzione come uguaglianza tra frazioni equivalenti $$ \frac{2}{8} = \frac{3}{12} $$ Essendo due frazioni equivalenti il prodotto in croce dei loro termini è lo stesso. $$ 2 \cdot 12 = 3 \cdot 8 $$ $$ 24 = 24 $$
Proprietà del comporre
- In una proporzione a:b=c:d
- la somma dei primi due termini (a+b) sta al primo termine (a) come la somma dei restanti due termini (c+d) sta al terzo termine (c) $$ (a+b):a = (c+d):c $$
- la somma dei primi due termini (a+b) sta al secondo termine (b) come la somma dei restanti due termini (c+d) sta al quarto termine (d) $$ (a+b):b = (c+d):d $$
Dimostrazione
Considero una proporzione
$$ a:b=c:d $$
Riscrivo la proporzione come uguaglianza tra due frazioni equivalenti
$$ \frac{a}{b} = \frac{c}{d} $$
Per la proprietà invariantiva delle equazioni sommo +1 in entrambi i membri dell'equazione
$$ \frac{a}{b} + 1 = \frac{c}{d} + 1 $$
$$ \frac{a+b}{b} = \frac{c+d}{d} $$
A questo punto riscrivo l'equazione sotto forma di proporzione e ottengo una formula del comporre.
$$ (a+b):b = (c+d):d $$
Per ottenere l'altra formula basta applicare la proprietà dell'invertire alla proporzione e ricominciare da capo
$$ a:b=c:d $$
Applico la proprietà dell'invertire e inverto i termini
$$ b:a=d:c $$
Poi trasformo la proporzione in un'uguaglianza tra frazioni equivalenti
$$ \frac{b}{a} = \frac{d}{c} $$
Per la proprietà invariantiva delle equazioni sommo +1 in entrambi i membri
$$ \frac{b}{a} + 1 = \frac{d}{c} + 1 $$
$$ \frac{a+b}{a} = \frac{c+d}{c} $$
Trasformo l'equazione in una proporzione e ottengo anche l'altra formula che volevo dimostrare
$$ (a+b):a = (c+d):c $$
Esempio. Considero la proporzione $$ 2:6 = 3:9 $$ Poi applico la proprietà del comporre
A] Secondo la proprietà del comporre anche (a+b):a = (c+d):c è una proporzione $$ (2+6):2 = (3+9):3 $$ $$ 8:2 = 12:3 $$ Per verificarlo calcolo il prodotto in croce $$ 8 \cdot 3 = 12 \cdot 2 $$ $$ 24 = 24 $$ L'identità è confermata. Quindi anche (2+6):2 = (3+9):3 è una proporzione.
B] Secondo la proprietà del comporre anche (a+b):b = (c+d):d è una proporzione $$ (2+6):6 = (3+9):9 $$ $$ 8:6 = 12:9 $$ Verifico tramite il prodotto in croce se quest'ultima è una proporzione $$ 8 \cdot 9 = 6 \cdot 12 $$ $$ 72 = 72 $$ L'identità è confermata. Anche (2+6):6 = (3+9):9 è una proporzione.
Proprietà dello scomporre
- In una proporzione a:b=c:d
- la differenza dei primi due termini (a-b) sta al primo termine (a) come la differenza dei restanti due termini (c-d) sta al terzo termine (c) $$ (a-b):a = (c-d):c $$
- la differenza dei primi due termini (a-b) sta al secondo termine (b) come la differenza dei restanti due termini (c-d) sta al quarto termine (d) $$ (a-b):b = (c-d):d $$
Dimostrazione
Considero una proporzione
$$ a:b=c:d $$
Una proporzione è l'uguaglianza tra due frazioni equivalenti
$$ \frac{a}{b} = \frac{c}{d} $$
Applico la proprietà invariantiva delle equazioni per sottrarre -1 in entrambi i membri dell'equazione
$$ \frac{a}{b} - 1 = \frac{c}{d} - 1 $$
$$ \frac{a-b}{b} = \frac{c-d}{d} $$
Riscrivo l'equazione in una proporzione e ottengo una formula dello scomporre.
$$ (a-b):b = (c-d):d $$
Per ottenere anche l'altra formula dello scomporre
$$ a:b=c:d $$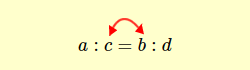
applico la proprietà dell'invertire alla proporzione e inverto i termini tra loro
$$ b:a=d:c $$
Poi riscrivo proporzione come uguaglianza tra frazioni equivalenti
$$ \frac{b}{a} = \frac{d}{c} $$
Per la proprietà invariantiva delle equazioni sottraggo -1 in entrambi i membri dell'equazione
$$ \frac{b}{a} - 1 = \frac{d}{c} - 1 $$
$$ \frac{a-b}{a} = \frac{c-d}{c} $$
Trasformo l'equazione in una proporzione e ottengo anche l'altra formula dello scomporre
$$ (a-b):a = (c-d):c $$
Esempio. Considero la proporzione $$ 4:2 = 10:5 $$ Poi applico la proprietà del scomporre
A] Secondo la proprietà del scomporre anche (a-b):a = (c-d):c è una proporzione $$ (4-2):4 = (10-5):10 $$ $$ 2:4 = 5:10 $$ Per verificare se è una proporzione calcolo il prodotto in croce $$ 2 \cdot 10 = 4 \cdot 5 $$ $$ 20 = 20 $$ L'identità è vera. Quindi anche (4-2):4 = (10-5):10 è una proporzione.
B] Secondo la proprietà del comporre anche (a-b):b = (c-d):d è una proporzione $$ (4-2):2 = (10-5):5 $$ $$ 2:2 = 5:5 $$ E' già evidente che è una proporzione... ma per completezza verifico con il prodotto in croce se anche quest'ultima è una proporzione $$ 2 \cdot 5 = 5 \cdot 2 $$ $$ 10 = 10 $$ L'identità è vera. Anche (4-2):2 = (10-5):5 è una proporzione.
Proprietà del permutare
Scambiando i termini medi in una proporzione a:b=c:d
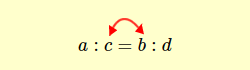
oppure i termini estremi
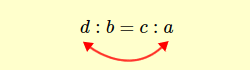
si ottiene ancora una proporzione
Dimostrazione
Considero una proporzione
$$ a:b=c:d $$
Una proporzione è l'uguaglianza tra due frazioni equivalenti
$$ \frac{a}{b} = \frac{c}{d} $$
Per la proprietà invariantiva delle equazioni moltiplico per b/c entrambi i membri dell'equazione
$$ \frac{a}{b} \cdot \frac{b}{c} = \frac{c}{d} \cdot \frac{b}{c} $$
$$ \frac{ab}{bc} = \frac{bc}{cd} $$
Poi semplifico le frazioni
$$ \require{cancel} \frac{a \cancel{b}}{\cancel{b}c} = \frac{b\cancel{c}}{\cancel{c}d} $$
$$ \frac{a}{c} = \frac{b}{d} $$
Riscrivo l'equazione come proporzione e ottengo la formula del permutare con i termini medi scambiati.
$$ a:c = b:d $$
Per ottenere anche l'altra formula seguo un percorso simile.
Considero di nuovo l'equazione iniziale
$$ \frac{a}{b} = \frac{c}{d} $$
Applico la proprietà invariantiva delle equazioni moltiplicando per d/a entrambi i membri dell'equazione
$$ \frac{a}{b} \cdot \frac{d}{a} = \frac{c}{d} \cdot \frac{d}{a} $$
$$ \frac{ad}{ab} = \frac{cd}{ad} $$
Poi semplifico le frazioni
$$ \require{cancel} \frac{\cancel{a}d}{\cancel{a}b} = \frac{c\cancel{d}}{a\cancel{d}} $$
$$ \frac{d}{b} = \frac{c}{a} $$
Riscrivo l'equazione come proporzione e ottengo anche l'altra formula del permutare, quella con i termini estremi scambiati.
$$ d:b = c:a $$
Esempio. Considero la proporzione $$ 3:9 = 4:12 $$ Poi applico la proprietà del permutare
A] Secondo la proprietà del permutare anche a:c =b:d è una proporzione $$ 3:4 = 9:12 $$ Per verificare se è una proporzione calcolo il prodotto in croce $$ 3 \cdot 12 = 4 \cdot 9 $$ $$ 36 = 36 $$ L'identità è vera. Quindi anche 3:4 = 9:12 è una proporzione.
B] Secondo la proprietà del permutare anche d:b = c:a è una proporzione $$ 12:9 = 4:3 $$ Verifico con il prodotto in croce se anche quest'ultima è una proporzione $$ 12 \cdot 3 = 4 \cdot 9 $$ $$ 36 = 36 $$ L'identità è vera. Anche 12:9 = 4:3 è una proporzione.
Proprietà dell'invertire
Invertendo ogni antecedente con il proprio conseguente in una proporzione a:b=c:d
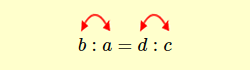
si ottiene ancora una proporzione
Dimostrazione
Considero una proporzione
$$ a:b=c:d $$
Una proporzione è l'uguaglianza tra due frazioni equivalenti
$$ \frac{a}{b} = \frac{c}{d} $$
Per la proprietà invariantiva delle equazioni moltiplico entrambi i membri per il termine d e semplifico.
$$ \frac{a}{b} \cdot d = \frac{c}{d} \cdot d $$
$$ \frac{a \cdot d}{b} = \frac{c}{\cancel{d}} \cdot \cancel{d} $$
$$ \frac{ad}{b} = c $$
Per la proprietà invariantiva delle equazioni moltiplico entrambi i membri per il termine b e semplifico.
$$ \frac{ad}{b} \cdot b = c \cdot b $$
$$ \frac{ad}{ \cancel{b}} \cdot \cancel{b} = bc $$
$$ ad = bc $$
Per la proprietà invariantiva delle equazioni moltiplico entrambi i membri per 1/a e semplifico.
$$ ad \cdot \frac{1}{a} = bc \cdot \frac{1}{a} $$
$$ \cancel{a}d \cdot \frac{1}{ \cancel{a} } = \frac{bc}{a} $$
$$ d = \frac{bc}{a} $$
Per la proprietà invariantiva delle equazioni moltiplico entrambi i membri per 1/c e semplifico.
$$ d \cdot \frac{1}{c} = \frac{bc}{a} \cdot \frac{1}{c} $$
$$ \frac{d}{c} = \frac{b \cancel{c}}{a} \cdot \frac{1}{\cancel{c}} $$
$$ \frac{d}{c} = \frac{b}{a} $$
Riscrivo l'equazione come proporzione e ottengo anche l'altra formula dell'invertire, quella con i termini antecedenti e conseguenti invertiti tra loro.
$$ d:c = b:a $$
Esempio. Considero la proporzione $$ 2:6 = 4:12 $$ Poi applico la proprietà del permutare invertendo i termini antecedenti e conseguenti tra loro $$ 6:2 = 12:4 $$ Per verificare se anche quest'ultima è una proporzione calcolo il prodotto in croce dei termini $$ 6 \cdot 4 = 12 \cdot 2 $$ $$ 24 = 24 $$ L'identità è vera. Quindi anche 6:2 = 12:4 è una proporzione.
E così via.
