Diedro

Un diedro è una figura geometrica formata dall'intersezione di due semipiani, detti "facce", che hanno origine da una retta comune detta "spigolo".

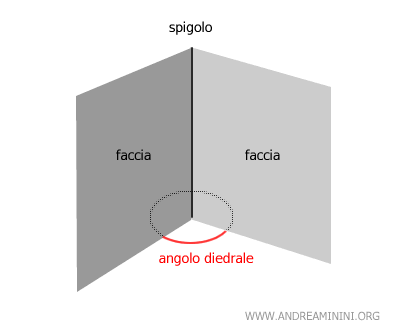
E' un concetto dello spazio a tre dimensioni della geometria solida.

I due semipiani dividono lo spazio in due regioni o parti. Ognuna delle due parti è un diedro.

Le facce del diedro costituiscono il contorno o superficie del diedro.

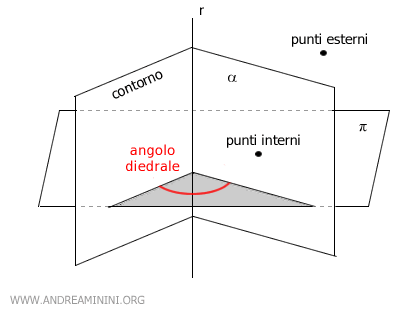
I punti del diedro non appartenenti alla superficie sono detti punti interni del diedro.

L'angolo tra i due semipiani, rispetto a un piano π, è chiamato angolo diedrale. Può essere concavo o convesso.

Se il piano π è perpendicolare allo spigolo (r), l'angolo diedrale è detto sezione normale del diedro.

La differenza tra diedro e poliedro. Un diedro è uno spazio delimitato da due semipiani che hanno in comune una retta e un angolo. Un poliedro, invece, è un corpo solido limitato da piani, chiamati "facce". Le linee in cui due facce si incontrano sono chiamate "spigoli" e i punti in cui tre o più spigoli si incontrano sono chiamati "vertici". Ad esempio, sono poliedri il cubo, la piramide, il prisma, ecc. In sintesi, mentre un diedro è definito da due piani e un angolo, un poliedro è un solido tridimensionale con molte facce piane.

La sezione del diedro

La sezione del diedro è l'angolo ottenuto dall’intersezione fra il diedro e un piano che interseca lo spigolo.

In pratica, la sezione è la proiezione dell’angolo del diedro su un determinato piano.

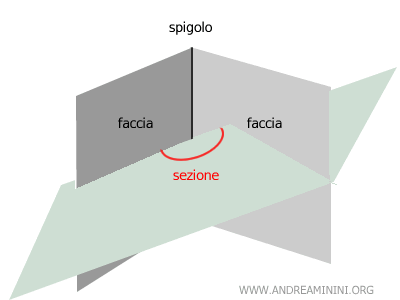
Questo prova che l’equivalente del diedro nella geometria piana è l’angolo.

In particolar modo la sezione è detta “sezione normale” quando il piano che interseca il diedro è perpendicolare allo spigolo.

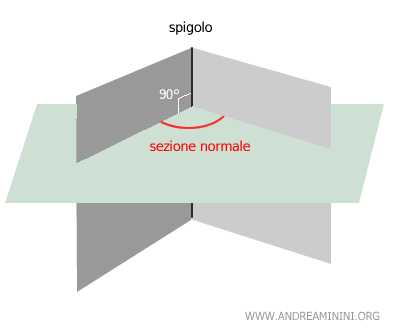
Dalla sezione normale del diedro derivano tutte le sue caratteristiche.

Ad esempio, la sezione normale mi permette di capire se il diedro è convesso o concavo

• Diedro convesso
  Un diedro convesso non contiene i prolungamenti delle sue facce. La sezione normale è inferiore a 180°.
• Diedro concavo
  Un diedro convesso contiene i prolungamenti delle sue facce. La sezione normale è superiore a 180°.

Nota. Quando l'ampiezza della sezione normale è precisamente di 180°, equivalente a un angolo piatto, il diedro diventa un piano che si interseca perpendicolarmente con un altro. In questo caso, la sezione corrisponde alla retta formata dall'intersezione dei due piani e il diedro è detto diedro piatto (180°). Quando le facce sono coincidenti, invece, il diedro è detto diedro giro se comprende tutti i punti dello spazio oppure diedro nullo se non comprende alcun punto interno.

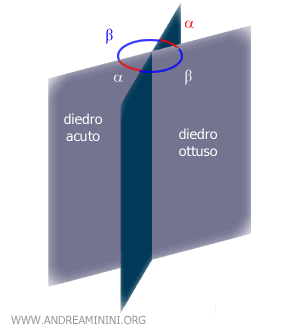
A seconda dell’ampiezza dell’angolo della sezione, il diedro è anche detto retto (90°), ottuso (>90°) o acuto (<90°).

• Diedro retto
  Un diedro retto ha una sezione normale di 90°. E' esattamente la metà di un diedro piatto.
• Diedro acuto
  I diedri con una sezione normale inferiore a 90° sono detti diedri acuti.
• Diedro ottuso
  I diedri con una sezione normale superiore a 90° e inferiore a 180° sono detti diedri ottusi.
  

In base alla loro sezione normale due diedri possono essere complementari, supplementari o esplementari.

• Diedri complementari
  Due diedri sono detti diedri complementari quando la loro somma è un diedro retto (90°).
• Diedri supplementari
  Due diedri sono detti diedri supplementari se la loro somma è un diedro piatto (180°).
• Diedri esplementari
  Due diedri sono detti diedri esplementari se la loro somma è un diedro giro (360°).

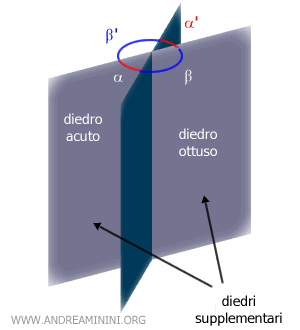
Esempio. I diedri α e β sono diedri supplementari perché la loro somma è un diedro piatto (180°).

La congruenza tra diedri

Due diedri sono diedri congruenti quando hanno la stessa sezione normale.

Si può anche dire che due diedri sono congruenti se e solo se sono sovrapponibili tramite dei movimenti rigidi.

In ogni caso, due diedri congruenti hanno le loro sezioni normali congruenti.

 

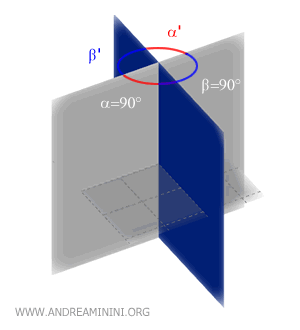
Esempio. I diedri α e β sono diedri congruenti α≅β perché hanno la stessa sezione normale (90°).

Diedri opposti allo spigolo

Due diedri sono detti diedri opposti allo spigolo se hanno uno spigolo in comune e le facce di un diedro sono il prolungamento delle facce degli altri.

Ad esempio, gli angoli α e α' sono angoli opposti allo spigolo.

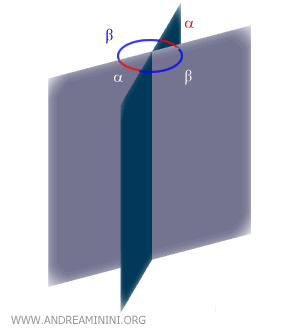
Due diedri opposti allo spigolo sono sempre congruenti.

Così come accade nel piano con gli angoli opposti al vertice.

Diedri consecutivi e adiacenti

I diedri sono classificati in consecutivi e adiacenti in base alla loro posizione relativa

• Diedri consecutivi
  Due diedri sono diedri consecutivi se hanno in comune lo spigolo e una faccia.
• Diedri adiacenti
  Due diedri sono diedri adiacenti se sono consecutivi e le facce non comuni sono semipiani opposti.

  Nota. Due diedri adiacenti sono anche supplementari perché la somma dei loro angoli diedrali è pari a 180°. Ad esempio, i diedri α e β sono diedri consecutivi perché condividono lo stesso spigolo e una faccia. Sono anche diedri adiacenti perché le loro facce sono opposte.
  
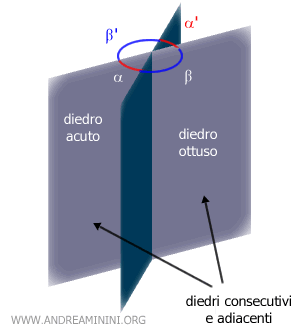
  Anche i diedri α e β', i diedri α' e β' e i diedri α' e β sono adiacenti per gli stessi motivi. Viceversa, la coppia di diedri α e α' non sono diedri consecutivi.

Osservazioni

Alcune osservazioni e note

• Due piani non paralleli generano quattro diedri, ossia due coppie di diedri opposti allo spigolo.
• Due piani sono perpendicolari se formano quattro diedri retti
  Poiché gli angoli diedri opposti allo spigolo sono congruenti, è sufficiente che uno dei diedri sia retto perché lo siano anche gli altri.
  
• Due semipiani che condividono uno spigolo dividono lo spazio in due diedri esplementari, perché la somma dei loro angoli diedrali è pari a 360°. Se i due diedri non sono piatti, allora uno di questi diedri ha un angolo diedrale minore di 180° (convesso) e l'altro ha un angolo diedrale maggiore di 180° (concavo).
  
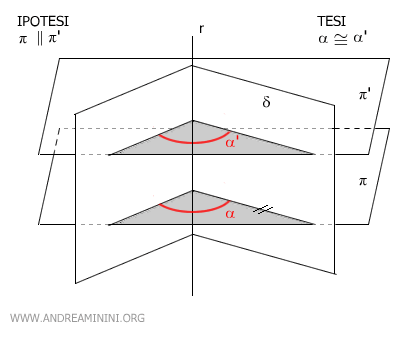
• Le sezioni parallele di un diedro sono congruenti tra loro
  Le sezioni parallele π e π' del diedro δ hanno lo stesso angolo diedrale α≅α'.
  
• La somma di due diedri consecutivi è un diedro che ha lo stesso spigolo e le facce non comuni.

E così via.