Gli angoloidi

Un angoloide è una figura geometrica solida che si forma nello spazio a tre dimensioni considerando un poligono e un punto V fuori dal piano del poligono, in cui tutte le semirette che hanno origine dal punto V e passano per i punti del poligono.
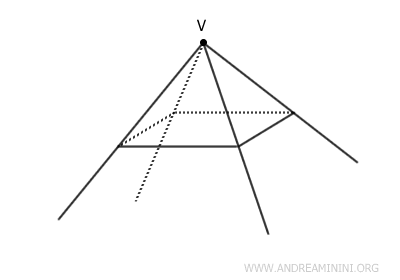
un esempio di angoloide

L'angoloide non ha una "superficie chiusa" nel senso tradizionale, poiché le semirette si estendono all'infinito.

E' una generalizzazione di un angolo nello spazio tridimensionale.

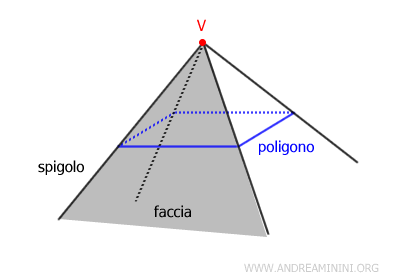
le componenti di un angoloide

Un angoloide ha le seguenti componenti principali

Vertice (V)
È l'origine unica da cui emergono tutte le semirette che definiscono l'angoloide.
Spigoli
Queste sono le semirette che partono dal vertice V e passano attraverso i vertici del poligono. Ogni spigolo è definito dalla sua intersezione con un vertice del poligono.
Facce
Sono gli angoli formati da due spigoli consecutivi con il vertice VV come punto comune. Ciascuna faccia dell'angoloide corrisponde a un angolo del poligono sul quale si basa l'angoloide.

Un angoloide definito da n spigoli ha n facce ed è detto ennaedro (o n-edro) indefinito.

Ad esempio, un triedro è un angoloide formato da tre spigoli e tre facce.

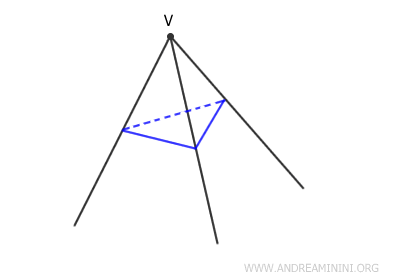
esempio di triedro

L'angoloide è detto regolare se tutte le facce sono uguali.

Nota. Spesso gli angoloidi sono usati per descrivere le proiezioni, le ombre e fenomeni come la rifrazione della luce.

Tipi di spigoli in un angolide

L'angoloide, con una base poligonale e un unico vertice, ha due tipi di spigoli:

Spigoli laterali
Questi spigoli collegano il vertice dell'angoloide ai vertici della base. Ciascuno di questi spigoli è condiviso da due facce laterali adiacenti.
Spigoli di base
Sono gli spigoli che appartengono al poligono di base. Ogni spigolo di base è la frontiera tra due facce laterali e la base.

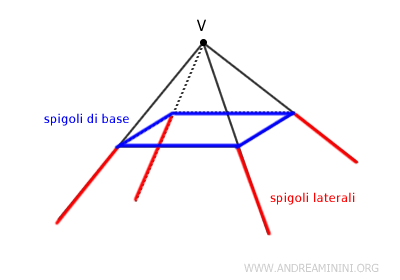
Nota. Quando si parla di spigoli di un angoloide bisogna fare molta attenzione alla notazione usata dai libri. Alcuni testi intendono solo gli spigoli laterali mentre altri si riferiscono a tutti gli spigoli (laterali + base).

Osservazioni

Alcune osservazioni è note sugli angoloidi

Il numero di spigoli laterali presenti in un angoloide è uguale al numero di vertici del poligono sottostante
Se il poligono ha $ n $ lati, l'angoloide ha $ n $ spigoli laterali.
Nota. Considerando anche gli spigoli base oltre agli spigoli laterali, il numero complessivo di spigoli di un angoloide è uguale al doppio dei vertici $ n $ del poligono ossia $ 2n $
Il numero delle facce laterali dell'angoloide è uguale al numero di angoli del poligono sottostante
Ogni lato del poligono genera una faccia laterale che passa per quel lato e il vertice dell'angoloide. Poiché il poligono ha $ n $ lati e quindi $ n $ angoli interni, ci saranno $ n $ facce laterali nell'angoloide.
Nota. Considerando anche la faccia di base, un angoloide ha complessivamente $ n+1 $ facce.
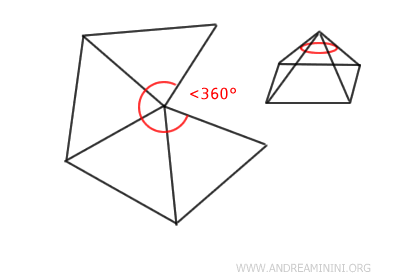
In un angoloide la somma degli angoli di ogni faccia è inferiore a un angolo giro (360°)
Se la somma delle ampiezze degli angoli fosse esattamente 360°, l'angoloide si appiattirebbe degenerando in un piano
Ogni spigolo dell'angoloide dà origine a un diedro formato da due facce consecutive
Un diedro è l'angolo solido formato dall'intersezione di due facce lungo un spigolo comune. In un angoloide ogni spigolo laterale genera un diedro formato dalle due facce che lo condividono. Ogni spigolo di base, invece, forma un diedro composto da una faccia laterale e la faccia di base.
Quanti diedri si formano in un angoloide? Considerando anche la faccia di base, il numero totale di diedri in un angoloide è pari al numero totale di spigoli, ovvero $ 2n $ se la base ha $ n $ lati: $ n $ diedri tra facce laterali e $ n $ diedri tra facce laterali e la base.
In un angoloide la somma degli angoli intorno al vertice è minore di un angolo giro
Se la somma fosse uguale a un angolo giro, il vertice apparterrebbe al piano in cui è contenuto il poligono di base. Questo implicherebbe che il vertice non appartiene a un solido tridimensionale. In questo caso i semipiani si dispongono completamente su un unico piano.
In ogni angoloide l'angolo di una faccia è minore della somma degli altri angoli rimanenti
L'affermazione è analoga alla disuguaglianza triangolare, che stabilisce che in un triangolo qualsiasi la lunghezza di un lato è sempre minore della somma degli altri due. Qui, però, il concetto è tridimensionale e si applica agli angoli diedri di un angoloide invece che ai lati di un triangolo.
Dimostrazione. Devo dimostrare che in un angoloide ogni angolo è minore della somma degli altri, cioè che per ogni angolo $ \alpha_k $ tra quelli presenti nell'angoloide, vale la relazione: \[ \alpha_k < \sum_{j \neq k} \alpha_j \] In altre parole, dato un angoloide con angoli al vertice $ \alpha_1, \alpha_2, ..., \alpha_n $, devo dimostrare che per ogni $ k $ scelto: \[ \alpha_k < \alpha_1 + \alpha_2 + ... + \alpha_{k-1} + \alpha_{k+1} + ... + \alpha_n \] Sapendo che la somma di tutti gli angoli di un angoloide è sempre minore di 360°: \[ \alpha_1 + \alpha_2 + \dots + \alpha_n < 360^\circ \] Questa è una proprietà fondamentale degli angoloidi e rappresenta il punto di partenza della dimostrazione. Prendo un angolo arbitrario $ \alpha_k $. Posso separarlo nella somma totale: \[ \alpha_k + (\alpha_1 + \alpha_2 + \dots + \alpha_{k-1} + \alpha_{k+1} + \dots + \alpha_n) < 360^\circ \] Chiamo la somma degli altri angoli (escluso $ \alpha_k $) con la lettera $ S $: \[ S = \alpha_1 + \alpha_2 + \dots + \alpha_{k-1} + \alpha_{k+1} + \dots + \alpha_n \] Quindi posso riscrivere la disuguaglianza come: \[ \alpha_k + S < 360^\circ \] A questo punto confronto $ S $ e $ \alpha_k $ \[ \alpha_k + S < 360^\circ \] Sapendo anche che la somma di tutti gli angoli dell'angoloide è minore di $ 360^\circ $, quindi anche la somma parziale $ S $ (che non include $ \alpha_k $) sarà minore di $ 360^\circ $. $$ S < 360° $$ Ora, voglio dimostrare che: \[ S > \alpha_k \] Dove $ S $ rappresenta la somma di tutti gli angoli tranne $ \alpha_k $. Sottraggo $ \alpha_k $ da entrambi i membri della diseguaglianza: \[ \alpha_k + S < 360^\circ \] \[ \alpha_k + S - \alpha_k < 360^\circ - \alpha_k \] \[ S < 360^\circ - \alpha_k \] Poiché $ S<360° $, la quantità $ 360^\circ - \alpha_k $ è maggiore di $ S $ solo se $ \alpha_k < S $. Dunque, ottengo: \[ \alpha_k < S \] Sostituendo il valore di $ S $: \[ \alpha_k < \alpha_1 + \alpha_2 + \dots + \alpha_{k-1} + \alpha_{k+1} + \dots + \alpha_n \] \[ \alpha_k < \sum_{j \neq k} \alpha_j \] Ho così dimostrato che in un angoloide qualsiasi angolo è minore della somma degli altri angoli rimanenti. Questo segue direttamente dal fatto che la somma totale è minore di 360° e che gli angoli sono positivi.
In un triedo l'angolo di una faccia è maggiore della differenza degli altri due angoli rimanenti
Questo deriva direttamente dalle proprietà della somma degli angoli in un angoloide.
Dimostrazione. Un triedo è una figura tridimensionale formata da tre semipiani che si intersecano lungo tre semirette con un vertice comune. Se chiamo gli angoli diedri tra le facce $ \alpha, \beta, \gamma $, allora so già che la loro somma è sempre minore di 360°: \[ \alpha + \beta + \gamma < 360^\circ \] Matematicamente, devo dimostrare che per ogni angolo $ \alpha, \beta, \gamma $ vale la disuguaglianza: \[ \alpha > |\beta - \gamma| \] \[ \beta > |\alpha - \gamma| \] \[ \gamma > |\alpha - \beta| \] Per dimostrare questa proprietà, posso ragionare in modo simile alla disuguaglianza triangolare, applicata agli angoli. Dalla relazione $ \alpha + \beta + \gamma < 360^\circ $, posso dire che ogni angolo è più piccolo della somma degli altri due: \[ \alpha < \beta + \gamma \] \[ \beta < \alpha + \gamma \] \[ \gamma < \alpha + \beta \] Queste sono disuguaglianze fondamentali che derivano dalla proprietà degli angoloidi. Considero ora la differenza tra due angoli. Ad esempio, prendo $ \alpha $ e $ \beta $, con $ \gamma $ la terza faccia: \[ \alpha > | \beta - \gamma | \quad \text{se e solo se} \quad \alpha + \gamma > \beta \] Questo è vero perché ho già dimostrato sopra che $ \beta < \alpha + \gamma $. Analogamente, posso scrivere: \[ \beta > | \alpha - \gamma | \] \[ \gamma > | \alpha - \beta | \] Il valore assoluto è necessario perché, se $ \beta > \gamma $, allora la differenza $ \beta - \gamma $ è positiva, mentre se $ \beta < \gamma $, la differenza $ \beta - \gamma $ è negativa, e devo considerare il valore assoluto. Questo dimostra che in un triedo, ogni angolo è sempre maggiore della differenza degli altri due.

E così via.