La somma e la differenza di solidi
La geometria solida studia figure tridimensionali, dette solidi, e le operazioni tra queste. Tra le operazioni, c'è anche la somma e la differenza di solidi che rappresentano due modalità fondamentali per combinare o sottrarre volumi.
La somma di solidi
La somma di due solidi A e B privi di punti interni comuni (cioè disgiunti, oppure con solo qualche punto in comune sui contorni), è il solido C formato dall’unione di tutti i punti che appartengono a A o a B. $$ A+B=C $$
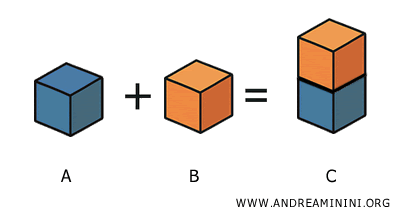
I solidi A e B si dicono parti del solido risultante C.
La somma di solidi gode di due proprietà fondamentali:
- Commutativa: l’ordine con cui si sommano i solidi non cambia il risultato $$ A+B=B+A=C $$
- Associativa: la somma di più solidi non dipende dall’ordine delle operazioni $$ (A+B)+C = A+(B+C) $$
Queste proprietà rendono l’operazione di somma utile nella suddivisione e ricomposizione di oggetti complessi, come avviene nel calcolo del volume o nella modellazione 3D.
Esempio
Considero due cubi: uno di lato 3 cm e uno di lato 2 cm, posti vicini senza toccarsi.
La loro somma C sarà un nuovo solido che include entrambi i cubi come parti distinte.
Il volume totale sarà la somma dei loro volumi:
\[ V = 3^3 + 2^3 = 27 + 8 = 35\ \text{cm}^3 \]
La differenza di solidi
La differenza tra due solidi A e B è definita come il solido C tale che: $$ C = A-B $$ cioè, è ciò che rimane di A togliendo B.
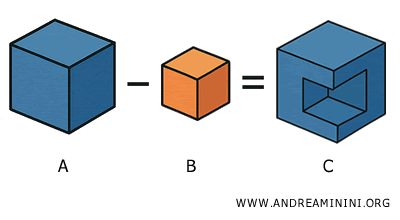
Affinché la differenza sia ben definita, il solido B deve essere contenuto interamente o parzialmente in A.
Esempio
Considero due cubi: uno di lato 3 cm e uno di lato 2 cm.
In questo caso il cubo di lato 2 cm è incavato all’interno del cubo più grande, centrato al suo interno.
La differenza C = A B è un cubo cavo, con un foro interno. Il volume rimanente sarà:
\[ V = 3^3 - 2^3 = 27 - 8 = 19\ \text{cm}^3 \]
E così via.
